Current page:
I am a member of Herbert Edelsbrunner's research group at IST Austria. I did my PhD with the research group Discrete Differential Geometry at the University of Göttingen.
Discrete/Computational Geometry/Topology, Algorithms, Combinatorics.
| |
IST Austria Object 1, Floor 2 Computer Science Am Campus 1 3400 Klosterneuburg Austria |
Vox: +43 (0)2243 9000-3302 Net: lastname (at) ist.ac.at |

|
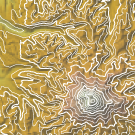
Optimal topological simplification of discrete functions on surfaces Ulrich Bauer, Carsten Lange, and Max Wardetzky. Discrete and Computational Geometry 47:2 (2012), 347–377. Abstract: Given a function f on a surface and a tolerance δ > 0, we construct a function fδ subject to ‖fδ - f‖∞ ≤ δ such that fδ has a minimum number of critical points. Our construction relies on a connection between discrete Morse theory and persistent homology and completely removes homological noise with persistence ≤ 2δ from the input function f. The number of critical points of the resulting simplified function fδ achieves the lower bound dictated by the stability theorem of persistent homology. We show that the simplified function can be computed in linear time after persistence pairs have been computed. [pdf] [doi] |
|
Persistence in discrete Morse Theory PhD thesis, University of Göttingen, 2011. [link] [pdf] |
|
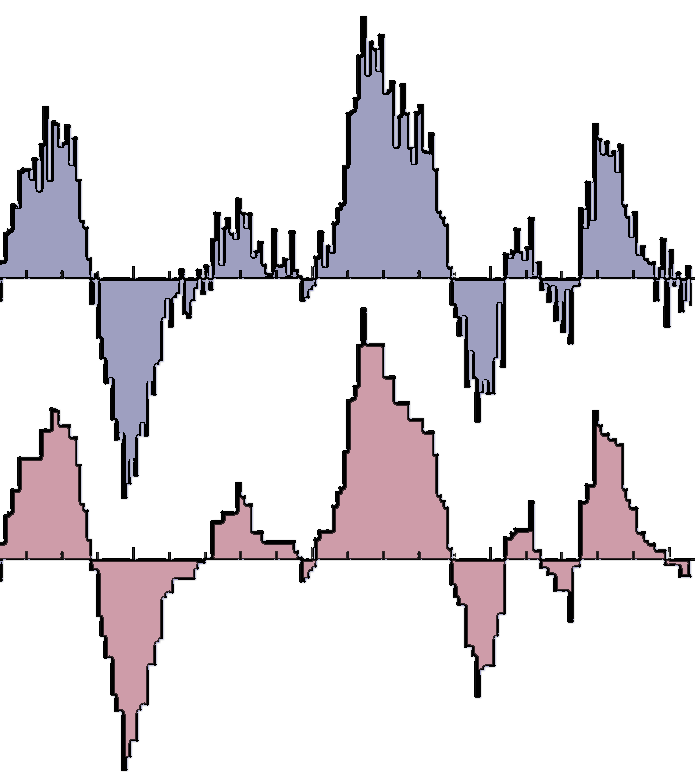
Total Variation Meets Topological Persistence: A First Encounter Ulrich Bauer, Carola-Bibiane Schönlieb, and Max Wardetzky. Proceedings of ICNAAM 2010, pp. 1022-1026. Abstract: We present first insights into the relation between two popular yet apparently dissimilar approaches to denoising of one dimensional signals, based on (i) total variation (TV) minimization and (ii) ideas from topological persistence. While a close relation between (i) and (ii) might phenomenologically not be unexpected, our work appears to be the first to make this connection precise for one dimensional signals. We provide a link between (i) and (ii) that builds on the equivalence between TV-L2 regularization and taut strings and leads to a novel and efficient denoising algorithm that is contrast preserving and operates in O(nlogn) time, where n is the size of the input. [pdf] |
|
Uniform Convergence of Discrete Curvatures from Nets of Curvature Lines Ulrich Bauer, Konrad Polthier, Max Wardetzky, Discrete and Computational Geometry 43:4 (2010), 798–823. Abstract: We study “Steiner-type” discrete curvatures computed from nets of curvature lines on a given smooth surface, and prove their uniform pointwise convergence to smooth principal curvatures. We provide explicit error bounds, with constants depending only on the limit surface and the shape regularity of the discrete net. [pdf] [doi] |

|
Generating Parametric Models of Tubes from Laser Scans Ulrich Bauer, Konrad Polthier, Computer-Aided Design 41 (2009), 719–729. Conference version: Parametric Reconstruction of Bent Tube Surfaces, Proceedings NASAGEM/Cyberworlds 2007, pp. 465–474. [pdf] [doi] Abstract: We present a method for parametric reconstruction of a piecewise defined pipe surface, consisting of cylinder and torus segments, from an unorganized point set. Our main contributions are reconstruction of the spine curve of a pipe surface from surface samples, and approximation of the spine curve by G¹ continuous circular arcs and line segments. Our algorithm accurately outputs the parametric data required for bending machines to create the reconstructed tube. [pdf] [doi] |

|
Detection of Planar Regions in Volume Data for Topology Optimization Ulrich Bauer, Konrad Polthier, Proceedings of Geometry Modelling and Processing 2008, Lecture Notes in Computer Science vol. 4975 (2008), 119–126. Abstract: We propose a method to identify planar regions in volume data using a specialized version of the discrete Radon transform operating on a structured or unstructured grid. The algorithm uses an efficient discretization scheme for the parameter space to obtain a running time of O(N(T log T)), where T is the number of cells and N is the number of plane normals in the discretized parameter space. We apply our algorithm in an industrial setting and perform experiments with real-world data generated by topology optimization algorithms, where the planar regions represent portions of a mechanical part that can be built using steel plate. [pdf] [doi] |
|
Assignment Problem with Constraints Diploma Thesis – ETH Zürich (10/2004 – 03/2005) Abstract: Combinatorial optimisation plays an important role in logistics, and many of the basic problems and algorithms find a direct application in this area or even originate from it. For instance, the assignment problem asks for a cost-optimal assignment of workers to tasks or products to warehouse locations. Additional constraints on the solutions, such as an equal distribution of products to warehouses, are however often required in real-world settings. An algorithm to solve this problem is developed based on Bertsekas' well-known auction algorithm. Advisors: Andreas Weissl and Prof. Angelika Steger, ETH Zürich [pdf] |
|
Minimum Cycle Bases Algorithms for the Chemistry Development Kit Interdisciplinary project – TU München (04/2004 – 09/2004) The cycles of a graph (the subgraphs whose vertices have even degree) span a matroid; addition on this matroid is defined as the symmetric difference of the edges. A cycle basis is a maximal set of linearly independent cycles; a minimum cycle basis is a cycle basis with minimum edge count (or minimum total edge weight in the case of weighted graphs).The Smallest Set of Smallest Rings (SSSR), the chemical equivalent to a minimum cycle basis, plays an important role in computational chemistry. However, an efficient and exact algorithm for computing an SSSR was missing from the Chemistry Development Toolkit (CDK), a comprehensive library for computational chemistry which is used in several projects such as JMol and JChemPaint. We present details about the implementation of several algorithms related to minimum cycles bases and provide several improvements to the algorithms that lower the computational complexity of the minimum cycle basis algorithm to O(m³). Advisors: Franziska Berger and Prof. Peter Gritzmann, TU München [pdf] |

|
Hydra: Collaborative Text Editor Application development – TU München (01/2003 – 06/2003) Hydra is an easy-to-use collaborative real-time text editor for Mac OS X. It uses operational transformations to synchronise text on the different participating computers and allows users to simultaneously edit a text file without locking.Hydra has won several awards, among them the Apple Design Award and the O'Reilly Mac OS X Innovators Award. It is now a commercial product maintained by two of my co-authors under the name SubEthaEdit. 

|
