Knut Heidemann

I am now working as a research engineer at Fraunhofer IAIS, Sankt Augustin.

Research interests

Complex Systems, Network Theory, Machine Learning, Statistical Physics.

Publications

Refereed Articles

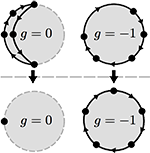
	Topology determines force distributions in one-dimensional random spring networks Knut M. Heidemann, Andrew O. Sageman-Furnas, Abhinav Sharma, Florian Rehfeldt, Christoph F. Schmidt, and Max Wardetzky. Phys. Rev. E 97, 022306, 2018. Abstract: Networks of elastic fibers are ubiquitous in biological systems and often provide mechanical stability to cells and tissues. Fiber reinforced materials are also common in technology. An important characteristic of such materials is their resistance to failure under load. Rupture occurs when fibers break under excessive force and when that failure propagates. Therefore it is crucial to understand force distributions. Force distributions within such networks are typically highly inhomogeneous and are not well understood. Here we construct a simple one-dimensional model system with periodic boundary conditions by randomly placing linear springs on a circle. We consider ensembles of such networks that consist of N nodes and have an average degree of connectivity z, but vary in topology. Using a graph-theoretical approach that accounts for the full topology of each network in the ensemble, we show that, surprisingly, the force distributions can be fully characterized in terms of the parameters (N,z). Despite the universal properties of such (N,z)-ensembles, our analysis further reveals that a classical mean-field approach fails to capture force distributions correctly. We demonstrate that network topology is a crucial determinant of force distributions in elastic spring networks. [PRE]
	Topology counts: force distributions in circular spring networks Knut M. Heidemann, Andrew O. Sageman-Furnas, Abhinav Sharma, Florian Rehfeldt, Christoph F. Schmidt, and Max Wardetzky. Phys. Rev. Lett. 120, 068001, 2018. Abstract: Filamentous polymer networks govern the mechanical properties of many biological materials. Force distributions within these networks are typically highly inhomogeneous, and, although the importance of force distributions for structural properties is well recognized, they are far from being understood quantitatively. Using a combination of probabilistic and graph-theoretical techniques, we derive force distributions in a model system consisting of ensembles of random linear spring networks on a circle. We show that characteristic quantities, such as the mean and variance of the force supported by individual springs, can be derived explicitly in terms of only two parameters: (i) average connectivity and (ii) number of nodes. Our analysis shows that a classical mean-field approach fails to capture these characteristic quantities correctly. In contrast, we demonstrate that network topology is a crucial determinant of force distributions in an elastic spring network. Our results for 1D linear spring networks readily generalize to arbitrary dimensions. [PRL]
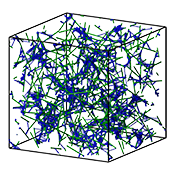
	Elasticity of 3D networks with rigid filaments and compliant crosslinks Knut M. Heidemann, Abhinav Sharma, Florian Rehfeldt, Christoph F. Schmidt, and Max Wardetzky. Soft Matter, 11(2), pp. 343–354, 2015. Abstract: Disordered filamentous networks with compliant crosslinks exhibit a low linear elastic shear modulus at small strains, but stiffen dramatically at high strains. Experiments have shown that the elastic modulus can increase by up to three orders of magnitude while the networks withstand relatively large stresses without rupturing. Here, we perform an analytical and numerical study on model networks in three dimensions. Our model consists of a collection of randomly oriented rigid filaments connected by flexible crosslinks that are modeled as wormlike chains. Due to zero probability of filament intersection in three dimensions, our model networks are by construction prestressed in terms of initial tension in the crosslinks. We demonstrate how the linear elastic modulus can be related to the prestress in these networks. Under the assumption of affine deformations in the limit of infinite crosslink density, we show analytically that the nonlinear elastic regime in 1- and 2-dimensional networks is characterized by power-law scaling of the elastic modulus with the stress. In contrast, 3-dimensional networks show an exponential dependence of the modulus on stress. Independent of dimensionality, if the crosslink density is finite, we show that the only persistent scaling exponent is that of the single wormlike chain. We further show that there is no qualitative change in the stiffening behavior of filamentous networks even if the filaments are bending-compliant. Consequently, unlike suggested in prior work, the model system studied here cannot provide an explanation for the experimentally observed linear scaling of the modulus with the stress in filamentous networks. [pdf]
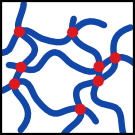
	Elastic response of filamentous networks with compliant crosslinks A. Sharma, M. Sheinman, K. M. Heidemann, and F. C. MacKintosh. Physical Review E 88, 052705 (2013). Abstract: Experiments have shown that elasticity of disordered filamentous networks with compliant crosslinks is very different from networks with rigid crosslinks. Here, we model and analyze filamentous networks as a collection of randomly oriented rigid filaments connected to each other by flexible crosslinks that are modeled as wormlike chains. For relatively large extensions we allow for enthalpic stretching of crosslink backbones. We show that for sufficiently high crosslink density, the network linear elastic response is affine on the scale of the filaments' length. The nonlinear regime can become highly nonaffine and is characterized by a divergence of the elastic modulus at finite strain. In contrast to the prior predictions, we do not find an asymptotic regime in which the differential elastic modulus scales linearly with the stress, although an approximate linear dependence can be seen in a transition from entropic to enthalpic regimes. We discuss our results in light of recent experiments. [pdf] [doi]

Thesis

On the mechanics of biopolymer networks Knut M. Heidemann, PhD Thesis, University of Göttingen, 2016. Abstract: In this thesis, we study the mechanical properties of biopolymer networks. We discuss which of these properties can be described by continuum approaches and which features, on the contrary, require consideration of the discrete nature or the topology of the network. For this purpose, we combine theoretical modeling with extensive numerical simulations. In Chapter 2, we study the elasticity of disordered networks of rigid filaments connected by flexible crosslinks that are modeled as wormlike chains. Under the assumption of affine deformations in the limit of infinite crosslink density, we show analytically that the nonlinear elastic regime in 1- and 2-dimensional networks is characterized by power-law scaling of the elastic modulus with the stress. In contrast, 3-dimensional networks show an exponential dependence of the modulus on stress. Independent of dimensionality, if the crosslink density is finite, we show that the only persistent scaling exponent is that of the single wormlike chain. Our theoretical considerations are accompanied by extensive quasistatic simulations of 3-dimensional networks, which are in agreement with the analytical theory, and show additional features like prestress and the formation of force chains. In Chapter 3, we study the distribution of forces in random spring networks on the unit circle by applying a combination of probabilistic theory and numerical computations. Using graph theory, we find that taking into account network topology is crucial to correctly capture force distributions in mechanical equilibrium. In particular, we show that application of a mean field approach results in significant deviations from the correct solution, especially for sparsely connected networks. [pdf]