aktualisiert: 3.9.2012
Gymnasium St. Xaver

Gymnasium St. Xaver Kurse Mathematik


Schuljahr 2012/13

Differential- und Integralrechnung:

Im Internet finden sich zahlreiche Tools zur Berechnung von Ableitungen und Stammfunktionen: Lineare Algebra und Analytische Geometrie:
Facharbeit
Informationen der Bezirksregierung.

Jeder Schüler, der bei mir eine Facharbeit schreiben möchte, sollte rechtzeitig mit mir Kontakt aufnehmen damit gemeinsam ein geeignetes Thema gefunden werden kann. Es ist möglich eigene Themen vorzuschlagen, oder im Gespräch gemeinsam ein Thema zu finden.

Ablauf:
1. Eine grobe Formulierung des Themas finden
2. Literatur zu dem Thema finden. Das Internet reicht nicht aus, es ist notwendig eine Bibliothek aufzusuchen
3. Präzise Formulierung des Themas
4. Schreiben der Facharbeit

Jeder sollte mindestens 3 Gesprächs-Termine vereinbaren. (auch per email!) Möglich sind:
Mo 4. Stunde und ab 15:30
Di 3. Stunde und ggf. Nachmittags
Mi 3. Stunde und 8./9. Stunde
Do 1.-2. Stunde und 5.-6. Stunde, 9. Stunde
Fr 3. und 5. Stunde. 8.-9. Stunde

Die Facharbeit im GK oder LK ersetzt eine Klausur. In Hinblick auf die Abiturprüfung wird angeraten, die Klausur freiwillig mitzuschreiben. Informationen der Bezirksregierung.

Kriterien: Die Arbeit muß mit eigenen Worten selbst verfasst und geschrieben sein. Inhaltlich und methodisch sollte das Thema auf Höhe des fachlichen Unterrichts der Jahrgangsstufe 12 bearbeitet werden. Die benutzten Quellen (z.B. Bücher, Zeitschriftenartikel, Internetseiten) müssen angegeben sein.

Eine Auswahl möglicher Themen: Anwendungsbezogene Themen sind auch möglich: Historische Themen sind gern willkommen, jedoch muß auch ein gewisser Mindestanteil an Mathematik enthalten sein.

Formelsatz. Beim Schreiben mathematischer Texte tritt die Frage auf, wie man Formeln schreibt. Professionell nennt man dies Formelsatz. Hierfür gibt es zwei Möglichkeiten: Bei einer Facharbeit in Informatik ist das Schreiben der Arbeit mit dem programmierten Text-Satz-Sytem LaTeX Voraussetzung. Es zeigt, ob die Grundprinzipien der Programmierung verstanden sind. Facharbeiten, die mit dem unzureichenden Hilfs-Programm WORD geschrieben sind, genügen nicht den Anforderungen des Faches Informatik.

Mathematische Puzzle

Puzzle können helfen schwierige mathematische Sachverhalte zu veranschaulichen:



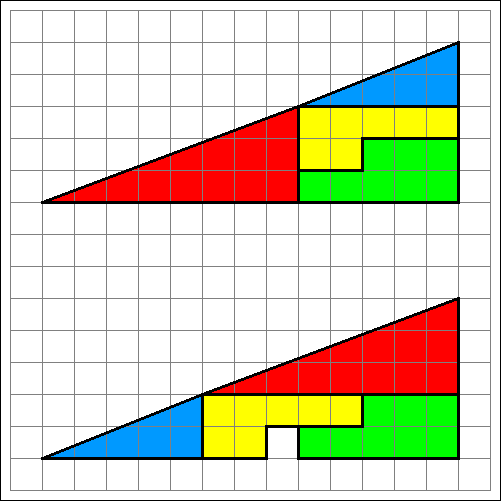
Woher kommt das fehlende weiße Quadrat in der untersten Reihe?

Das folgende Puzzle liefert einen geometrischen Beweis für die Summenformel der ersten n Quadratzahlen:

Rubik-Würfel

Arbeitsblatt zur Würfel-Sprache und Anleitung zum Ordnen des Würfels mit Formeln: Download
Der Rubik-Würfel (1975) des ungarischen Bauingenieurs und Architekten Ernö Rubik ist ein sehr lohnenswertes mathematisches Spielzeug. Es werden folgende Fertigkeiten trainiert: logisches Denkvermögen, räumliches Vorstellungsvermögen, fehlerfreies Arbeiten mit Termen, Schnelligkeit und Ausdauer, Fingerfertigkeit. Außerdem wird möglicherweise das erste Mal der Nutzen einer formalen Sprache für praktische Dinge wirklich erkannt.

Ästhetik und Schönheit der Mathematik

Natürlich hat auch die Mathematik eine ästhetische Seite:

Hinter diesen Fraktalen steckt richtig schöne und spannende Mathematik.

Querverbindungen zu anderen Fächern

Philosophie

Das Höhlengleichnis von Platon

Bereits Platon hat um 400 v.Chr. in seiner Akademie wichtige Erfahrungen beim Lehren und Lernen der Mathematik gemacht. Die dabei auftretenden Schwierigkeiten lassen sich auch heute noch kaum besser als in seinem Höhlengleichnis veranschaulichen:

Die wichtige Erkenntnis dabei: Augen auf und genau hingucken was man in unserer Welt sieht! Dabei versuchen zu erkennen was hinter den Dingen steckt.

Kunst

Schon sehr alt ist die Beziehung zur Kunst. Bekannt ist die Melancholia I von Albrecht Dürer (1514):

Der Mathematiker Felix Klein untersuchte an einer Kopie des Apoll von Belvedere ob es einen Zusammenhang zwischen mathematischen Eigenschaften einer Fläche und ihrem ästhetischen Reiz besteht.

Humor in der Mathematik

Die Mathematik ist kein trockenes Gebiet. Dieser Aspekt wird durch zahlreiche Witze und Cartoons unterstrichen. Sehr lesenswert ist das Buch von Friedrich Wille Humor in der Mathematik
Für die Mathematik, die Königin der Wissenschaften, hat dies der bedeutende Mathematiker John Edensor Littlewood (1885-1977), am pointiertesten ausgedrückt: "Ein guter mathematischer Scherz ist allemal besser - sogar in mathematischer Hinsicht - als ein ganzes Dutzend mittelmäßiger gelehrter Abhandlungen."
Carina öffnet die Tür zur höheren Mathematik: Tür steht ein Spalt offen, dahinter die Mathematik.

Mathematische Strenge


Nachdem Aristoteles um 350 v.Chr. die formale Logik, und somit die strenge Grundlage der Mathematik begründet hat, finden sich bei Euklid in seinen Elementen erste Versuche mathematischer Strenge durch Axiomatisierung und systematische Deduktion. Nach einer längeren Periode der Stagnation kam es im Zeitalter der beginnenden Industrialisierung zu einem enormen Aufschwung der mathematischen Wissenschaften. Erst zu Beginn des 19. Jahrhundert wurde diese Ekstase des stark zunehmenden Fortschritts durch ein Bedürfnis nach Sicherung und Klarheit der Ergebnisse unterlegt. So haben besonders Gauß, Cauchy und Weierstraß das griechische Ideal noch übertreffend, wieder die Strenge Behandlung der Mathematik eingeführt.
Ab 1870 erteilte Weierstraß der 20-jährigen Sofia Kowalewskaja Privatunterricht. 1884 wurde sie Professor für Mathematik in Stockholm.

Literatur

In der Geschichte waren Mathematiker manchmal eng mit literarischen und musischen Kreisen verwoben: Gelegentlich findet man hier auch Perlen der Weltliteratur:
Sehr lesenswert ist die Erzählung der Mathematikerin und Schriftstellerin Sonja Kowalewsky (1850-1891): Erinnerungen an meine Kindheit, Weimar 1960 (antiquarisch 3 bis 4 EUR).

Zitate

Es ist nicht das Wissen, sondern das Lernen, nicht das Besitzen, sondern das Erwerben, nicht das Dasein, sondern das Hinkommen, was den größten Genuß gewährt. (Carl Friedrich Gauß)
Alle Pädagogen sind sich darin einig: Man muß vor allem tüchtig Mathematik treiben, weil ihre Kenntnis fürs praktische Leben größten direkten Nutzen gewährt. (Felix Klein)
Die Mathematik muß man schon deswegen studieren, weil sie die Gedanken ordnet. (M.W. Lomonossow)
Die Mathematik ist eine wunderbare Lehrerin für die Kunst, die Gedanken zu ordnen, Unsinn zu beseitigen und Klarheit zu schaffen. (J.H. Fabre)
Das Denken gehört zu den größten Vergnügungen der menschlichen Rasse. (B. Brecht)
Die Mathematik ist eine Art Spielzeug, welches die Natur uns zuwarf zum Troste und zur Unterhaltung in der Finsternis. (Jean-Jacques Rousseau)
Mathematik allein befriedigt den Geist durch ihre außerordentliche Gewißheit. (Johannes Kepler)
Gleichungen sind wichtiger für mich, weil die Politik für die Gegenwart ist, aber eine Gleichung etwas für die Ewigkeit. (Albert Einstein)
Die Natur ist in der Sprache der Mathematik geschrieben. (Galileo Galilei)
Ein Beweis, der nicht streng ist, ist nichts. (Henri Poincaré)
Stefan Krämer (skraemer * math.uni-goettingen.de) Neuer Link: http://num.math.uni-goettingen.de/~skraemer