The step-1 tutorial program

Table of contents
Introduction The commented program Declarations of kernel wrapper functions Device Functions Device Function: lex_index_2D Device Function: global_pos Kernel Kernel: __single_thread_cholesky Parallelization of Cholesky Factorization Kernel: factorize_diagonal_block Kernel: strip_update Kernel: diag_update Kernel: lo_update Function: single_thread_cholesky Function: cholesky_impl Function: cholesky Class: CUDADriver Constructor: CUDADriver Destructor: ~CUDADriver Function: factorize Function: single_thread_cholesky Class: CholeskyTest Klasse: Cholesky Constructor: CholeskyTest Function: setup_and_assemble_test_matrix Function: run Function: cpu_tiled Function: LLtMult class: MyFancySimulation Function: precision_id Function: run Funktion: main	Results The plain program Declarations of kernel wrapper functions Device Functions Device Function: lex_index_2D Device Function: global_pos Kernel Kernel: __single_thread_cholesky Parallelization of Cholesky Factorization Kernel: factorize_diagonal_block Kernel: strip_update Kernel: diag_update Kernel: lo_update Function: single_thread_cholesky Function: cholesky_impl Function: cholesky Class: CUDADriver Constructor: CUDADriver Destructor: ~CUDADriver Function: factorize Function: single_thread_cholesky Class: CholeskyTest Klasse: Cholesky Constructor: CholeskyTest Function: setup_and_assemble_test_matrix Function: run Function: cpu_tiled Function: LLtMult class: MyFancySimulation Function: precision_id Function: run Funktion: main

Table of contents

Introduction
The commented program

Results
The plain program

Introduction

Cholesky Factorization

The Cholesky factorization can be used for solving a set of linear equations

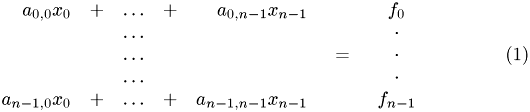
$\begin{eqnarray} \begin{array}{rcccr} a_{0,0}x_0 & + & \ldots & + & a_{0,n-1}x_{n-1} \\ & & \ldots & & \\ & & \ldots & & \\ & & \ldots & & \\ a_{n-1,0}x_0 & + & \ldots & + & a_{n-1,n-1}x_{n-1} \end{array} & = & \begin{array}{c} f_0 \\ \cdot\\ \cdot\\ \cdot\\ f_{n-1} \end{array} \end{eqnarray}$

with symmetric coeffizient matrix 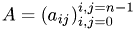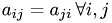$A = (a_{ij})_{i,j=0}^{i,j=n-1}$ , $a_{ij}=a_{ji}\,\forall i,j$ . The solution vector is denoted by 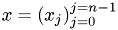$x=(x_j)_{j=0}^{j=n-1}$ and the right-hand side by 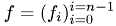$f=(f_i)_{i=0}^{i=n-1}$ . The factorization process yields a lower triangular matrix 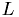$L$ , such that

$\begin{eqnarray} LL^T & = & A \,. \end{eqnarray}$

Solving the linear system is then achieved by solving two tringular systems of equations by forward and backward substitution. The first step yields the auxiliary solution 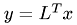$y = L^Tx$ .

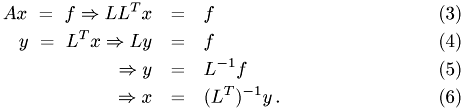
$\begin{eqnarray} Ax ~ = ~ f \Rightarrow LL^Tx & = & f \\ y ~ = ~ L^Tx \Rightarrow Ly & = & f \\ \Rightarrow y & = & L^{-1} f \\ \Rightarrow x & = & (L^T)^{-1} y \,. \end{eqnarray}$

Algorithm

The entries if 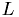$L$ follow from the condition 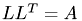$LL^T = A$ , that is

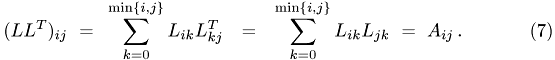
$\begin{eqnarray} (LL^T)_{ij} ~ = ~ \sum_{k=0}^{\min\{i,j\}} L_{ik}L^T_{kj} & = & \sum_{k=0}^{\min\{i,j\}} L_{ik}L_{jk} ~ = ~ A_{ij} \,. \end{eqnarray}$

The upper summation limit is due to the triangular shape of the matrix 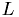$L$ which implies that one has to start computing its elements at the uppermost diagonal element and then has to proceed down the column. Only then one can go over to the next column. Therefore, the computation of the diagonal elements is inherently serial. Each diagonal element needs the entries of 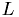$L$ , which are in the block above and left of it.

For the top row we have
1. $\begin{eqnarray} L_{00} & = & \sqrt{A_{00}} \end{eqnarray}$
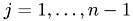2. do in parallel : $j = 1,\ldots, n-1$ :
  $\begin{eqnarray} L_{j0} & = & \frac{1}{\sqrt{L_{00}}} A_{0j} \end{eqnarray}$
and for the following rows
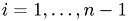
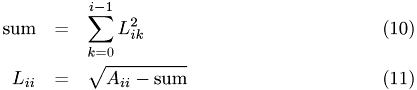
1. $\begin{eqnarray} \textrm{sum} & = & \sum_{k=0}^{i-1} L_{ik}^2 \\ L_{ii} & = & \sqrt{A_{ii} - \textrm{sum} } \end{eqnarray}$
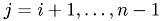2. do in parallel : $j = i+1,\ldots, n-1$ :
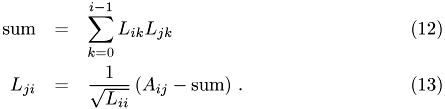
  $\begin{eqnarray} \textrm{sum} & = & \sum_{k=0}^{i-1} L_{ik}L_{jk} \\ L_{ji} & = & \frac{1}{\sqrt{L_{ii}}} \left( A_{ij} - \textrm{sum} \right) \,. \end{eqnarray}$

This shows, that at least the computation of the off-diagonal elements can be parallelized. Accidentally, that's the part which stands for most of the the computational costs in Cholesky factorization.

Special requirements due to CUDA

Hide latency of memory accesses, especially those to global memory
memory accesses require a certain order to be efficient (bank conflicts)
Kernels should load as little data from memory as possible and should do as much computations with it as possible
synchronisation. But that's always an issue in parallel programming

Literatur

Cambridge CUDA-Kurs Lecture 3 und 4

The commented program

 #ifndef CUDA_KERNEL_STEP_1_CU_H
 #define CUDA_KERNEL_STEP_1_CU_H

As the size of a half-warp is 16, this is the most efficient choice for the blocksize.

 #define TILE_SIZE 16

Declarations of kernel wrapper functions

 void single_thread_cholesky(float * A, int n_rows);
 
 void cholesky(float * A, int n_rows);
 cudaError_t factorize_diagonal_block(float *A,int block_offset, int global_row_length );
 
 void strip_update(float *A, int block_offset, int n_remaining_blocks, int n_rows_padded );
 
 void diag_update(float *A, int block_offset, int global_row_length, int n_remaining_blocks  );
 
 void lo_update(float *A, int block_offset, int n_blocks, int global_row_length, int n_remaining_blocks );
 
 #if __CUDA_ARCH__ >= 130
 void cholesky(double * a_d, int n_rows);
 cudaError_t factorize_diagonal_block(double *A,int block_offset, int global_row_length );
 
 void strip_update(double *A, int block_offset, int n_remaining_blocks, int n_rows_padded ) ;
 
 void diag_update(double *A, int block_offset, int global_row_length, int n_remaining_blocks  );
 
 void lo_update(double *A, int block_offset, int n_blocks, int global_row_length, int n_remaining_blocks );
 #endif
 
 
 
 #endif // CUDA_KERNEL_STEP_1_CU_H

Header-Datei der CUDA utility-Bibliothek.

 #include <cutil_inline.h>
 #include <cuda_kernel_wrapper_step-1.cu.h>

Device Functions

Before discussing the kernels we take a look at so-called device functions. They only execute on the GPU and up to CUDA 3.2 are automatically inline. But this is supposed to change.

Device Function: lex_index_2D

Compute a position 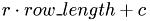$r\cdot row\_length + c$ in a linear array from a row index 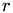$r$ and columnindex 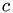$c$ of a matrix entry. It is assumed, that they matrix is stored row-wise.

Parameters:

	r	: row index
	c	: column index
	row_length	: number of matrix entries per row

 __device__ int lex_index_2D(int r, int c, int row_length)
 {
     return c +  r*row_length;
 }

Device Function: global_pos

Compute a global row or column index given the Block index and thread index.

Parameters:

	t_pos	: local row or comlumn index within block
	block_offset	: Index of the block in C-counting

 __device__ int global_pos(int t_pos, int block_offset)
 {
     return t_pos + TILE_SIZE*block_offset;
 }

Kernel

Kernel: __single_thread_cholesky

This kernel is supposed to be started only once and to compute the factorization of the whole matrix. This shows, that the source of of the CPU-based Cholesky factorization would also run unchanged on the GPU.

Parameters:

	A	: linear array containing rows of the matrix
	gpu_tile_size	: length of a row

 template<typename T>
 __global__
 void
 __single_thread_cholesky(T *A, const int gpu_tile_size)
 {

The outer loop runs of the rows L.

     for (unsigned int r = 0; r < gpu_tile_size; ++r)
     {

Compute diagonal entry of Cholesky factor.

             T sum = 0.;
             unsigned int idx;
             unsigned int idx_c;

Sum squares of entries computed so far in this row.

             for (unsigned int u = 0; u < r; ++u)
             {
                 idx = lex_index_2D(r, u, gpu_tile_size);
                 sum += A[idx] * A[idx];
             }
             idx = lex_index_2D(r, r, gpu_tile_size);
             A[idx] = sqrt(A[idx] - sum);

Off diagonal entries. Here, we exploit the symmetry of A. The auxiliary variable sum corresponds to step 2.1 of the algorithm given in the introduction.

             for (unsigned int c = r+1; c < gpu_tile_size; ++c)
             {
                     sum = 0.;
 
                     for (unsigned int u = 0; u < r; ++u)
                     {
                         idx_c = lex_index_2D(c, u, gpu_tile_size);
                         idx   = lex_index_2D(r, u, gpu_tile_size);
                         sum += A[idx_c]*A[idx];
                     }
 
                     idx_c = lex_index_2D(c, r, gpu_tile_size);
                     idx   = lex_index_2D(r, c, gpu_tile_size);
                     A[idx_c]  = A[idx] - sum;
 
                     idx   = lex_index_2D(r, r, gpu_tile_size);
                     A[idx_c] /= A[idx];
             }
     }
 }

Parallelization of Cholesky Factorization

Looking at the algorithm given in the introduction, we see that the main computational effort is caused by computing teh auxiliary variable sum in the update of the off-diagonal elements.

For an efficient parallelization we subdivide the matrix into blocks and start with factorizing the upper leftmost diagonal block. Afterwards we compute the blocks in the columns below the diagonal block. Finally, we update the lower right part of the matrix which is still to be factorized by subtracting the auxiliary variable sum. This happens in diag_update() und lo_update().

Kernel: factorize_diagonal_block

This kernel factorizes a diagonal block assuming that all previous diagonal blocks have already been factored.

In contrast to a serial implementation we hide the summation of the off-diagonal elements from the factorized part in the usage of the thread index and in the choice of synchroniazation points.

Each instance of this kernel computes one matrix entry of the Cholesky faktor 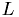$L$ .

Parameters:

	A	: MAtrix to factorize
	block_offset	: distance of the block which is to be factorized from the left uppermost diagonal block.
	global_row_length	: length of a row of .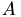

 template<typename T>
 __global__
 void
 __factorize_diagonal_block(T *A, int block_offset,
                            int global_row_length)
 {

In C arrays are stored row-wise thus, the 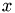$x$ coordinate of threadIdx indicates the column index.

     int col = threadIdx.x;

The 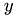$y$ coordinate of threadIdx indicates the row.

     int row = threadIdx.y;

From the thread and block index we have to compute the index of the matrix element this thread has to work on.

     int global_row = global_pos(row,block_offset);
     int global_col = global_pos(col,block_offset);
     int idx = lex_index_2D(global_row, global_col, global_row_length);

Copy the diagonal block to the shared memory so that threads can exchange their results. To avoid memory bank conflicts when consecutively acessing the elements of a column we add one column.

     __shared__ T L[TILE_SIZE][TILE_SIZE+1];

Copy a matrix entry from global to shared memory and synchronize.

     L[row][col]= A[idx];
     __syncthreads();
 
     T fac;

Compute the entries of the Cholesky faktors. We have to distinguish between diagonal elements i.e. 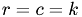$ r = c = k$ , elements of the uppermost row and the rest.

     for(int k=0;k<TILE_SIZE;k++)
     {
         __syncthreads();

Compute teh inverse square root of the diagonal element 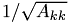$1/\sqrt{A_{kk}}$ store the result in a register. The function rsqrtf is documented in the CUDA Programming Guide.

         fac=rsqrtf(L[k][k]);
         __syncthreads();

Now compute the row on the right of the diagonal element

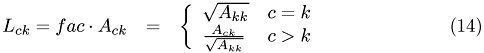
$\begin{eqnarray} L_{ck} = fac \cdot A_{ck} & = & \left\lbrace \begin{array}{ll} \sqrt{A_{kk}} & c = k \\ \frac{A_{ck}}{\sqrt{A_{kk}}} & c > k \end{array} \right. \end{eqnarray}$

This includs the computation of the diagonal element of the Cholesky factor.

         if ((row==k)&&(col>=k)) L[col][row]=(L[col][row])*fac;

Again we have to synchronize.

         __syncthreads();

Next, compute the lower left triangle.

The off-diagonal entries follow from

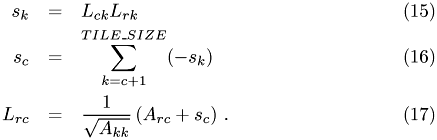
$\begin{eqnarray} s_k & = & L_{ck}L_{rk} \\ s_c & = & \sum_{k=c+1}^{TILE\_SIZE}(-s_k) \\ L_{rc} & = & \frac{1}{\sqrt{A_{kk}}} \left(A_{rc} + s_c \right)\,. \end{eqnarray}$

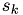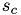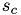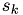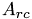We only have to perform the first of these steps, i.e. computing $s_k$ , and one addition in the sum. Hence, $s_c$ is computd incrementally by the k loop. Instead of storing $s_c$ , we subtract the individual terms $s_k$ from $A_{rc}$ and store the modified 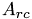$A_{rc}$ in the Cholesky factor.

At the time, when the condition row == k is true, L[row][col] contains the pre-computed value 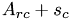$A_{rc} + s_c$ and multiplication with fac gives the fianl value 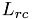$L_{rc}$ .

         if ((row>=col)&&(col>k)) L[row][col] -= L[col][k]*L[row][k];
     }
 
     __syncthreads();

Copy the result back to global memory.

     if (row>=col) A[idx] = L[row][col];
 }

Kernel: strip_update

This kernel updates 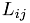$L_{ij}$ in the columsn below diagonal block j.

Parameters:

	A	: global Matrix
	block_offset	: distance from the digonal block just factorized.
	global_row_length	: length of a row of .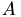

 template<typename T>
 __global__
 void
 __strip_update(T *A, int block_offset, int global_row_length)
 {

boffy und boffx are the coordinates of the matrix block this thread works on.

     int boffy=block_offset;

Die "+1" is needed, as block_offset denotes the position of the left uppermost block.

     int boffx = blockIdx.x + boffy + 1;

AS in the last kernel.

     int col = threadIdx.x;
     int row = threadIdx.y;

Again avoid bank conficts by adding a column

     __shared__ T topleft[TILE_SIZE][TILE_SIZE+1];
     __shared__ T workingmat[TILE_SIZE][TILE_SIZE+1];

Grab the data of the diagonal block just factorized ...

     int global_row = global_pos(row,block_offset);
     int global_col = global_pos(col,block_offset);
 
     int idx = lex_index_2D(global_row, global_col, global_row_length);
 
     topleft[row][col]=A[idx];

and the transposed Block which is to be processed

     global_row = global_pos(row,boffx);
     int idx_w = lex_index_2D(global_row, global_col, global_row_length);
     workingmat[col][row]= A[idx_w];
 
     __syncthreads();

Do step 2.2 of the algorithm givn in the introduction. Each thread works on one column.

     if(row==0)
         for (int k=0;k<TILE_SIZE;k++)
         {
             T sum=0.;
             for (int m=0;m<k;m++) sum += topleft[k][m]*workingmat[m][col];
 
             workingmat[k][col]=(workingmat[k][col] - sum)/topleft[k][k];
         }
 
     __syncthreads();
 
     A[idx_w] = workingmat[col][row];
 }

Kernel: diag_update

This Kernel computes the contribution of the last factorized diagonal block to the auxiliary variable sum in step 2.1.

Parameters:

	A	: global matrix
	block_offset	: Block-offset
	global_row_length	: length of a row of .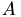

 template<typename T>
 __global__
 void
 __diag_update(T *A, int block_offset, int global_row_length)
 {

Finding the global indices and setup of the hared memors is as above.

     int boffx = blockIdx.x + block_offset + 1;
 
     int col = threadIdx.x;
     int row = threadIdx.y;
 
     int global_row = global_pos(row, boffx);
     int global_col = global_pos(col, block_offset);
 
     int idx = lex_index_2D(global_row, global_col, global_row_length);
 
     __shared__ T left[TILE_SIZE][TILE_SIZE+1];

Copy und synchronize.

     left[row][col]= A[idx];
 
     __syncthreads();

The thread with index (row, col) computes the corresponding term from step 2.1.

     T sum = 0.f;
 
     if(row>=col)
      {
         for(int kk=0; kk<TILE_SIZE; kk++) sum += left[row][kk]*left[col][kk];

Subtract the result from the global Matrix entry.

         global_col = global_pos(col, boffx);
         idx = lex_index_2D(global_row, global_col, global_row_length);
 
         A[idx] -= sum;
      }
 }

Kernel: lo_update

This kernel applies the intermedite results produced by strip_update() and diag_update() to the rest of the matrix.

Parameters:

	A	: global matrix
	block_offset	: Block-offset
	n_blocks	: Number of bloecks, in which a row of `A` is subdivided.
	global_row_length	: length of a row of `A`.

 template<typename T>
 __global__
 void
 __lo_update(T *A, int block_offset, int n_blocks, int global_row_length)
 {

Start with local und global Indices of the entry this thread works on ...

     int col = threadIdx.x;
     int row = threadIdx.y;
 
     int boffy=blockIdx.y+block_offset+1;
     int boffx=boffy+1;
 
     __shared__ T left[TILE_SIZE][TILE_SIZE];

The extra column is needed only for upt.

     __shared__ T upt[TILE_SIZE][TILE_SIZE+1];

Start reading data at the lower left.

     int global_row = global_pos(row, boffy);
     int global_col = global_pos(col, block_offset);
 
     int idx = lex_index_2D(global_row, global_col, global_row_length);
 
     upt[row][col]=A[idx];
 
     for (;boffx<n_blocks;boffx++)
     {
        global_row = global_pos(row, boffx);
        idx = lex_index_2D(global_row, global_col, global_row_length);
 
         left[row][col]=A[idx];
 
         __syncthreads();
 
         T matrixprod=0.f;

The thread with index (row, col) computes the corrsponding term from step 2.2.

         for (int kk=0;kk<TILE_SIZE;kk++)
             matrixprod+=left[row][kk]*upt[col][kk];
 
         __syncthreads();
 
         global_col = global_pos(col, boffy);
         idx = lex_index_2D(global_row, global_col, global_row_length);
 
         A[idx]-=matrixprod;
     }
 }

Function: single_thread_cholesky

This function wraps the kernel call. a_d : Pointer to device memory containing the matrix entries. n_rows : the number of rows of the matrix. This implies the number of columns and total number of elements as the matrix behind a_d is supposed to be square.

 template<typename T>
 void
 single_thread_cholesky(T * a_d, int n_rows)
 {

Start the kernel which is supposed to work only in one thread.

     __single_thread_cholesky<<<1,1>>>(a_d, n_rows);
 }

Function: cholesky_impl

This function wraps the kernel call.

 template<typename T>
 void
 _cholesky(T * a_d, int n_rows)
 {
     cudaError_t error;

Compute the number of blocks needed to cover the matrix.

     int n_blocks = (n_rows+int(TILE_SIZE)-1)/int(TILE_SIZE);
     int n_rows_padded = n_blocks*TILE_SIZE;

A thread-block should as large as a matrix block.

     dim3 threads(TILE_SIZE,TILE_SIZE);
 
     dim3 logrid;
 
     for(int i=n_blocks; i>2; --i)
     {
         logrid.x=1;
         logrid.y=i-2;
 
         dim3 stripgrid(i-1);
 
         __factorize_diagonal_block<<<1, threads>>>(a_d, n_blocks-i, n_rows_padded);
         cudaThreadSynchronize();
 
         __strip_update<<<stripgrid, threads>>>(a_d, n_blocks-i, n_rows_padded);
         cudaThreadSynchronize();
 
         __diag_update<<<stripgrid, threads>>>(a_d, n_blocks-i, n_rows_padded);
         cudaThreadSynchronize();
         __lo_update<<< logrid, threads >>>(a_d, n_blocks-i, n_blocks, n_rows_padded);
         cudaThreadSynchronize();
     }

For the last 2x2-Block submatrix lo_update() is not needed anymore.

     if(n_blocks>1)
     {
         __factorize_diagonal_block<<<1, threads>>>(a_d, n_blocks-2,
                                                    n_rows_padded);
         cudaThreadSynchronize();
 
         __strip_update<<<1, threads>>>(a_d, n_blocks-2, n_rows_padded);
         cudaThreadSynchronize();
 
         __diag_update<<<1, threads>>>(a_d, n_blocks-2, n_rows_padded);
         cudaThreadSynchronize();
     }

Factorize the last diagonal block.

     __factorize_diagonal_block<<<1, threads>>>(a_d, n_blocks-1, n_rows_padded);

Make all threads finish before the host is allowed to go on. Remeber, kernel starts are asynchronous.

     cudaThreadSynchronize();

... check error state of GPU.

     error=cudaGetLastError();
     if (error != cudaSuccess)
     {
        printf("     Error code %d: %s.\n",error,cudaGetErrorString(error));
        exit(-1);
     }
 }
 
 template<typename T>
 cudaError_t
 _factorize_diagonal_block(T * a_d, int block_offset, int n_rows_padded )
 {
     dim3 threads(TILE_SIZE,TILE_SIZE);
     __factorize_diagonal_block<<<1, threads>>>(a_d, block_offset, n_rows_padded);
         cudaThreadSynchronize();
 
            return cudaGetLastError();
 }
 
 
 template<typename T>
 void
  _strip_update(T *a_d, int block_offset , int n_remaining_blocks, int n_rows_padded )
 {
      cudaError_t error;
 
      dim3 stripgrid(n_remaining_blocks-1);
      dim3 threads(TILE_SIZE,TILE_SIZE);
     __strip_update<<<stripgrid, threads>>>(a_d, block_offset, n_rows_padded);

every update must be synchronized, because we can't continue factorizing befor knowing the updated submatrix of A

         cudaThreadSynchronize();
     error=cudaGetLastError();
     if (error != cudaSuccess)
     {
        printf("     Error code %d: %s.\n",error,cudaGetErrorString(error));
        exit(-1);
     }
 }
 
 template<typename T>
 void
 _diag_update(T *a_d, int block_offset, int n_rows_padded , int n_remaining_blocks )
 {
      cudaError_t error;
      dim3 stripgrid(n_remaining_blocks-1);
      dim3 threads(TILE_SIZE,TILE_SIZE);
  __diag_update<<<stripgrid, threads>>>(a_d, block_offset, n_rows_padded);
      cudaThreadSynchronize();
  error=cudaGetLastError();
  if (error != cudaSuccess)
  {
     printf("     Error code %d: %s.\n",error,cudaGetErrorString(error));
     exit(-1);
  }
 }
 
 template<typename T>
 void
 _lo_update(T *a_d, int block_offset, int n_blocks, int n_rows_padded, int n_remaining_blocks )
 {
      cudaError_t error;
      dim3 logrid;
      logrid.x=1;
      logrid.y=n_remaining_blocks-2;
      dim3 threads(TILE_SIZE,TILE_SIZE);
     __lo_update<<< logrid, threads >>>(a_d, block_offset, n_blocks, n_rows_padded);
         cudaThreadSynchronize();
     error=cudaGetLastError();
     if (error != cudaSuccess)
     {
        printf("     Error code %d: %s.\n",error,cudaGetErrorString(error));
        exit(-1);
     }
 }
 
 cudaError_t factorize_diagonal_block(float *A,int block_offset, int global_row_length )
 { return _factorize_diagonal_block(A, block_offset, global_row_length  );}
 
 void strip_update(float *A, int block_offset, int n_remaining_blocks, int n_rows_padded )
 {_strip_update(A, block_offset, n_remaining_blocks , n_rows_padded );}
 
 void diag_update(float *A, int block_offset, int global_row_length, int n_remaining_blocks  )
 {_diag_update(A, block_offset, global_row_length, n_remaining_blocks  );}
 
 void lo_update(float *A, int block_offset, int n_blocks, int global_row_length, int n_remaining_blocks )
 {_lo_update(A, block_offset, n_blocks, global_row_length, n_remaining_blocks  );}

Function: cholesky

This function provides the template specializations. Otherwise we get linker errors.

 void cholesky(float * a_d, int n_rows) { _cholesky(a_d, n_rows); }

Starting from compute capability 1.3 double precision is available, too. In order to be able to use it, we have to add the corresponding tempate specialization.

 #if __CUDA_ARCH__ >= 130
 void cholesky(double * a_d, int n_rows) { _cholesky(a_d, n_rows); }
 cudaError_t factorize_diagonal_block(double *A,int block_offset, int global_row_length )
 { return _factorize_diagonal_block(A, block_offset, global_row_length  );}
 
 void strip_update(double *A, int block_offset, int n_remaining_blocks, int n_rows_padded )
 {_strip_update(A, block_offset, n_remaining_blocks , n_rows_padded );}
 
 void diag_update(double *A, int block_offset, int global_row_length, int n_remaining_blocks  )
 {_diag_update(A, block_offset, global_row_length, n_remaining_blocks  );}
 
 void lo_update(double *A, int block_offset, int n_blocks, int global_row_length, int n_remaining_blocks )
 {_lo_update(A, block_offset, n_blocks, global_row_length, n_remaining_blocks  );}
 #endif
 
 
 
 #ifndef CUDADriver_STEP_1_H
 #define CUDADriver_STEP_1_H
 
 #include <lac/FullMatrixAccessor.h>
 #include <lac/blas++.h>
 
 #define __CUDA_ARCH__ 130

Each example program is put into a separate namespace so that it becomes easier to combine classes from different examples.

 namespace step1 {

Class: CUDADriver

This class is responsible for managing host-device communication, that is data transfer and invoking kernels. To simplify host-device data transfer, we use our cublas++-library which encapsulates all the details.

 template<typename T>
 class CUDADriver {
 
 public:

Some typedefs to make life easier.

     typedef typename blas_pp<T, cublas>::blas_wrapper_type BW;
     typedef typename blas_pp<T, cublas>::FullMatrixAccessor FullMatrixAccessor;
     typedef typename blas_pp<T, cublas>::Matrix Matrix;
     typedef typename blas_pp<T, cublas>::SubMatrix SubMatrix;
     typedef typename blas_pp<T, cublas>::MatrixSubCol MatrixSubCol;
     typedef typename blas_pp<T, cublas>::Vector Vector;
     typedef typename blas_pp<T, cublas>::SubColVector SubColVector;
     typedef typename blas_pp<T, cublas>::SubVectorBase SubVectorBase;
 
     typedef std::map<std::string,double> TimerName2Value;
 
 
 
     CUDADriver();
 
     ~CUDADriver ();
 
     double factorize(FullMatrixAccessor& A);
 
     double factorize(::FullMatrix<T> &A);
 
     void factorize(FullMatrixAccessor& A, TimerName2Value& times);
 
     void single_thread_cholesky(FullMatrixAccessor& A);
 
 
 private:
     Matrix A_d;
 
 };
 
 } // namespace step1 END
 
 #endif // CUDADriver_STEP_1_H
 
 
 
 #ifndef CUDA_DRIVER_STEP_1_HH
 #define CUDA_DRIVER_STEP_1_HH
 
 #include <base/CUDATimer.h>
 
 #include "cuda_driver_step-1.h"
 
 #include "cuda_kernel_wrapper_step-1.cu.h"
 
 #include <cutil_inline.h>
 
 #include <QTime>

Constructor: CUDADriver

The constructor of the driver class does not do much. At least in this case.

 template<typename T>
 step1::CUDADriver<T>::CUDADriver()
 {
 }

Destructor: ~CUDADriver

 template<typename T>
 step1::CUDADriver<T>::~CUDADriver()
 {
 }

Function: factorize

This function copies the data from the host to the device, starts the CUDA-based factorization and copies the result back to the host. A : Matrix to factorize

Returns:: { Number od seconds spent in GPU version of Cholesky factorization. NOT milliseconds. }

 template<typename T>
 double
 step1::CUDADriver<T>::factorize(FullMatrixAccessor& A)
 {

Copy from host to device

     this->A_d = A;
 
     QTime t;
     t.start();

Call the multi-threaded factorization. To this end, we have to grab dep into the Matrix object and retrieve the bare pointer to the array containing the matrix entries.

     cholesky(this->A_d.array().val(), this->A_d.n_rows() );

Convert milliseconds into seconds. Cf. QT-doc.

     double kernel_time = t.elapsed()/1000.;

Finally, copy the result from device back to host.

     A = this->A_d;
 
     return kernel_time;
 }

A : Matrix to factorize

 template<typename T>
 void
 step1::CUDADriver<T>::factorize(FullMatrixAccessor& A, TimerName2Value& times)
 {

Copy from host to device

     this->A_d = A;
 
     QTime t;

Call the multi-threaded factorization. To this end, we have to grab dep into the Matrix object and retrieve the bare pointer to the array containing the matrix entries.

Compute the number of blocks needed to cover the matrix.

         int n_blocks = (A.n_rows()+int(TILE_SIZE)-1)/int(TILE_SIZE);
         int n_rows_padded = n_blocks*TILE_SIZE;
 
         T* a_d = this->A_d.array().val();
 
         times["factorize_diagonal_block"] = 0.;
         times["strip_update"] = 0.;
         times["diag_update"] = 0.;
         times["lo_update"] = 0.;
 
         for(int i=n_blocks; i>2; --i)
         {
             t.restart();
             cudaError_t error = factorize_diagonal_block(a_d, n_blocks-i, n_rows_padded);

t.stop();

             times["factorize_diagonal_block"]+=t.elapsed();
 
             AssertThrow(error == cudaSuccess, ::ExcMessage( cudaGetErrorString(error) ) );
 
 
             t.restart();
             strip_update(a_d, n_blocks-i, i , n_rows_padded);

t.stop();

             times["strip_update"]+=t.elapsed();
 
             t.restart();
             diag_update(a_d, n_blocks-i, n_rows_padded, i);

t.stop();

             times["diag_update"]+=t.elapsed();
 
             t.restart();
             lo_update(a_d, n_blocks-i, n_blocks, n_rows_padded,i);

t.stop();

             times["lo_update"]+=t.elapsed();
         }

For the last 2x2-Block submatrix lo_update() is not needed anymore.

         if(n_blocks>1)
         {
             factorize_diagonal_block(a_d, n_blocks-2, n_rows_padded);
 
             strip_update(a_d, n_blocks-2, 2, n_rows_padded);
 
             diag_update(a_d, n_blocks-2, n_rows_padded,  2);
         }

Factorize the last diagonal block.

         factorize_diagonal_block(a_d, n_blocks-1, n_rows_padded);
 
     }

Finally, copy the result from device back to host.

     A = this->A_d;
 
 }

Function: single_thread_cholesky

Factorization using only one thread. Demonstrates that CUDA can be basically used like C. A : Matrix to factorize

 template<typename T>
 void
 step1::CUDADriver<T>::single_thread_cholesky(FullMatrixAccessor& A)
 {

Copy from host to device

     this->A_d = A;

Call the single-threaded factorization. To this end, we have to grab dep into the Matrix object and retrieve the bare pointer to the array containing the matrix entries.

     single_thread_cholesky(this->A_d.array().val(), this->A_d.n_rows() );

Finally, copy the result from device back to host.

     A = this->A_d;
 }
 
 #endif // CUDA_DRIVER_STEP_1_HH

STL header

 #include <iostream>
 #include <vector>

 #include <QThread>
 #include <QTime>

deal.II-Komponenten

 #include <base/convergence_table.h>
 #include <lac/full_matrix.h>

include <lac/vector.h>

Treiber fuer den GPU-Teil. Binden alle sonstigen benoetigten header-Dateien ein.

 #include "cuda_driver_step-1.h"
 #include "cuda_driver_step-1.hh"
 
 #include <lac/FullMatrixAccessor.h>
 #include <lac/MatrixCreator.h>

define SinglePrecision

 namespace step1 {

Class: CholeskyTest

Triggers the Cholesky factorization in a separate thread. To this end we have to inherit from QThread und to overwrite the run()-Function. Number : type of matrix entries.

 template<typename Number>
 class CholeskyTest : public QThread
 {

We want to print only small matrices to the console.

     static const unsigned int max_display_size = 20;
 
 public:
 
     CholeskyTest(int n_r, ::ConvergenceTable& s_table);
 
 protected:
 
     void setup_and_assemble_test_matrix();
 
     void factorize();
 
     void check_results();
 
     void run();
 
     int n_rows;
 
     ::ConvergenceTable & speedup_table;
 
     ::FullMatrix<Number> A, L, L_T;
 
 };

Klasse: Cholesky

CPU-based Cholesky factorization.

 class Cholesky {
 
 
 
 public:
     template<typename T> static void cpu(std::vector<std::vector<T> > & A);
 
     template<typename T/ *, int tile_size* /> static void cpu_tiled(T* A, int tile_size);
 
     template<typename T> static void LLtMult(T * A, const T * L, int n_rows);
 };

Constructor: CholeskyTest

 template<typename Number>
 CholeskyTest<Number>::CholeskyTest(int n_r, ::ConvergenceTable& s_table)
 :
     n_rows(n_r),
     speedup_table(s_table)
 {}

Function: setup_and_assemble_test_matrix

 template<typename Number>
 void CholeskyTest<Number>::setup_and_assemble_test_matrix()
 {
     this->A.reinit(n_rows, n_rows);
     this->L.reinit(n_rows, n_rows);
     this->L_T.reinit(n_rows, n_rows);
 
     QTime t;
 
     this->speedup_table.add_value("n rows", n_rows);
 
     std::cout << "Initial Cholesky factor deal.II :" << std::endl;
     std::cout << "----------------------------------------------------"
               << std::endl;
 #ifdef nUSE_HADAMARD
     t.start();

Because of the design of the Tmmult-function of class FullMatrix we have to compute the transpose of the Referenz Cholesky factor 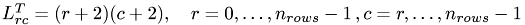$L^T_{rc} = (r+2)(c+2), \quad r = 0,\ldots , n_{rows}-1\,, c = r,\ldots , n_{rows}-1$

     for (unsigned int r = 0; r < n_rows; ++r)
         for (unsigned int c = r; c <n_rows; ++c)
             L(r,c) = 1e-0*(r+2)*(c+2);
     qDebug("Time for CPU-based setup of Cholesky factor : %f s",
            t.elapsed()/1000.);
 
     if ( L.n_rows() < max_display_size)
         L.print(std::cout, 10, 5);
     if ( L.n_rows() < max_display_size)
         std::cout << std::endl;std::cout << std::endl;
 
     {

Reinitialize timer for measuring copy time.

         t.restart();
         L_T.copy_from(L);
         qDebug("Time for CPU-based copying of Cholesky factor : %f s",
                t.elapsed()/1000.);

Compute 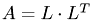$A = L\cdot L^T$ .

         t.restart();
         L_T.Tmmult(A, L, false);
         qDebug("Time for CPU-based multiplication of Cholesky factor"
                " : %f s",
                t.elapsed()/1000.);

The Matrix A is backed up, as its recomputation is pretty expensive.

         L_T.copy_from(A);
     }
     std::cout << "Matrix to factorize :" << std::endl;
     std::cout << "----------------------------------------------------"
             << std::endl;
     if ( A.n_rows() < max_display_size)
         A.print(std::cout, 10, 5);
     if ( A.n_rows() < max_display_size)
         std::cout << std::endl;std::cout << std::endl;
 #else
     MatrixCreator::extended_hadamard(n_rows, A);
 #endif
 
 }

Function: run

Initialization and factorization.

 template<typename Number>
 void CholeskyTest<Number>::run()
 {

Prepare the test data.

     this->setup_and_assemble_test_matrix();

Timer

     QTime t;
 double cpu_time, gpu_time;

Execute CPU-based Cholesky factorization.

     t.restart();
     {

We need the temporary object A_h to get access to the value array of A.

         FullMatrixAccessor<Number> A_h(A);
         Cholesky::cpu_tiled<Number>(A_h.val(), A_h.n_rows() );
     }
 
     cpu_time =  t.elapsed()/1000.;
     qDebug("Time for CPU-based Cholesky factorization : %f s",
            cpu_time);

Save timing results in a deal.II convergence table.

     this->speedup_table.add_value("CPU factorization", cpu_time);
     this->speedup_table.set_precision("CPU factorization", 10);
 
 
     std::cout << "CPU-factorized Matrix (lower triangle contains "
             << "transposed Cholesky factor) :" << std::endl;
     std::cout << "----------------------------------------------------"
             << std::endl;
     if ( A.n_rows() < max_display_size)
     A.print(std::cout, 10, 5);
 
 
     std::cout << "Matrix to factorize on GPU :" << std::endl;
     std::cout << "----------------------------------------------------"
             << std::endl;
     if ( A.n_rows() < max_display_size)
     A.print(std::cout, 10, 5);
     std::cout << std::endl;std::cout << std::endl;
 
     Assert( A.n_rows() == A.n_cols(),
            ::ExcMessage("Matrix not square! Cholesky impossible"));
 
 
     double kernel_time = 0;

compute the Cholesky factorization on the GPU.

     CUDADriver<Number> run;
     t.restart();
     {
         FullMatrixAccessor<Number> A_h(A, true);
         kernel_time = run.factorize(A_h);
     }
     gpu_time =  t.elapsed()/1000.;

For the impatient user dump the results to screen.

     qDebug("Time for GPU-based Cholesky factorization %f"
            " including data transfer : %f s\n"
            "speed up factor factorization : %f netto : %f n_rows : %d\n",
             kernel_time,
             gpu_time,
             cpu_time/kernel_time,
             cpu_time/gpu_time,
             n_rows);
 
     this->speedup_table.add_value("pure GPU fac", kernel_time);
     this->speedup_table.set_precision("pure GPU fac", 10);
 
     this->speedup_table.add_value("GPU fac incl data transfer", gpu_time);
     this->speedup_table.set_precision("GPU fac incl data transfer", 10);
 
 
     std::cout << "GPU-factorized Matrix (lower triangle contains "
               << "transposed Cholesky factor) :" << std::endl;
     std::cout << "----------------------------------------------------"
             << std::endl;
     if ( A.n_rows() < max_display_size)
         A.print(std::cout, 10, 5);

Timing of individual components of the factorization in order // to compare manual version against CUBLAS-based variant

     typename CUDADriver<Number>::TimerName2Value times;
     {
         FullMatrixAccessor<Number> A_h(A, true);
         run.factorize(A_h, times);
     }
 
 
     typename CUDADriver<Number>::TimerName2Value::const_iterator e=times.begin(), end_t=times.end();
     for( ; e != end_t ; ++e) {
 
         this->speedup_table.add_value(e->first, e->second);
         this->speedup_table.set_precision(e->first,10);
     }
 
 
     return;
 }

Function: cpu_tiled

T must be float or double.

Parameters:

: Matrix to factorize. factorization is in-place. Entries must be in the upper triangle including the diagonal.

The Cholesky-Factor will be stored in the lower triangle and overwrites the diagonal. This function is identical to the __singe_thread_cholesky() kernel.

 template<typename T>
 void Cholesky::cpu_tiled(T* A, int tile_size)
 {
 
         for (unsigned int r = 0; r < tile_size; ++r)
         {

Compute diagonal entry.

                 T sum = 0.;
                 unsigned int idx;
                 unsigned int idx_c;
 
                 for (unsigned int u = 0; u < r; ++u)
                 {
                     idx = r*tile_size + u;
                     sum += A[idx] * A[idx];
                 }
                 idx = r*tile_size + r;
                 A[idx] = sqrt(A[idx] - sum);
 
                 for (unsigned int c = r+1; c < tile_size; ++c)
                 {
                         T tmp = 0.;
 
                         for (unsigned int u = 0; u < r; ++u)
                         {
                             idx_c = c*tile_size + u;
                             idx   = r*tile_size + u;
                             tmp += A[idx_c]*A[idx];
                         }
 
                         idx_c = c*tile_size + r;
                         idx   = r*tile_size + c;
                         A[idx_c]  = A[idx] - tmp;
                         A[idx_c] /= A[r*tile_size + r];
 
                 }
         }
 }

Function: LLtMult

Computes the original matrix.

Parameters:

	A	: Pointer to value array of matrix
	L	: Pointer to value array of Cholesky factor
	n_rows	: Number of rows

 template<typename T>
 void Cholesky::LLtMult(T * A, const T * L, int n_rows)
 {
     for (unsigned int r = 0; r < n_rows; ++r)
         for (unsigned int c = 0; c <=r; ++c)
         {
             unsigned int idx = c + (r*(r+1))/2;
             unsigned int k_max = std::min(r,c);
 
             A[idx] = 0.;
 
             for (unsigned int k = 0; k < k_max; ++k)
             {
                 unsigned int idx_k   = k + (r*(r+1))/2;
                 unsigned int idx_k_T = k + (c*(c+1))/2;
                 A[idx] += L[idx_k]*L[idx_k_T];
             }
         }
 
 }

class: MyFancySimulation

Driver for the simulation.

 template<typename Number>
 class MyFancySimulation {
 
 public:
 
     MyFancySimulation() {}
 
     void run();
 
     static std::string precision_id();
 
 };

Function: precision_id

Returns a string for identifying the precision.

 template<>
 std::string MyFancySimulation<float>::precision_id()
 {
     return "float";
 }
 
 template<>
 std::string MyFancySimulation<double>::precision_id()
 {
     return "double";
 }
 
 
 
 }

Function: run

Compute the factorization for different matrix sizes.

 template<typename Number>
 void step1::MyFancySimulation<Number>::run()
 {   
     for (int n_min = 256; n_min < 513; n_min+=1024)
     {
         ::ConvergenceTable factorization_times;
 
         for (int n = n_min; n < n_min+768; n+=256)
         {
             CholeskyTest<Number> driver(n, factorization_times);
 
             driver.start();

for debugging purposes it is sometimes useful to disable the inheritance from QThread and to call the run()-function directly. driver.run();

             driver.wait();
 
         }
 
         std::ostringstream filename;
 
         filename << "chol_fac_times_" << n_min << "_" << precision_id().c_str() << ".dat";
 
         std::ofstream out(filename.str().c_str());
 
         factorization_times.write_text(out);
     }
 
 
     std::cout << "Fertig." << std::endl;
 }

Funktion: main

Instantiate and execute the simulation.

 int main(int / *argc* /, char * / *argv* /[])
 {
 
     using namespace step1;
 
     MyFancySimulation<float> machma_float;
 
     machma_float.run();
 
 
     MyFancySimulation<double> machma_double;
 
     machma_double.run();
 
 }

Results

We compare the Cholesky factorization on a Macbook Pro with Core2Duo processor running at 2.53 GHz and NVidias Gforce 8600m GT chip. Neglecting the time needed for host-to-device memory transfer the break even is at roughly 170 rows. Including transfer times this rise to 700 rows. The Cholesky factorization does not take into account any information about the size of the matrix entries. Therefore, the choice of testmatrix does not really matter as long as only timing tests are performed. Due to the fact, that GPUs have a different rounding behavior, one should also test whether for a given matrix and right-hand side the solution obtained from both variants is the same up to numerical accuracy.

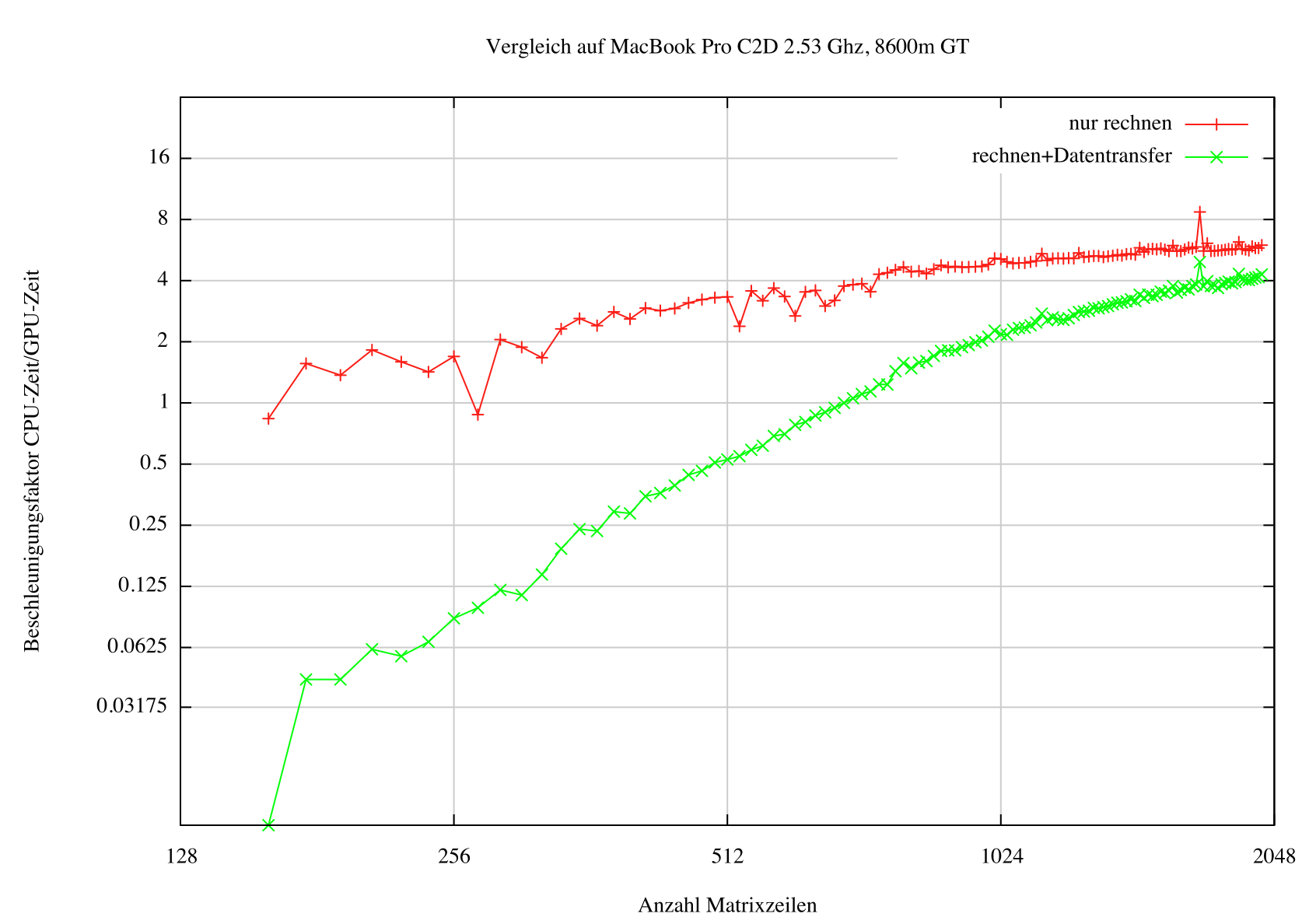
cholesky_macbookpro_c2d_2.53GHz_8600m_GT.png

Comparison of GPU vs. CPU performance for various matrix sizes.

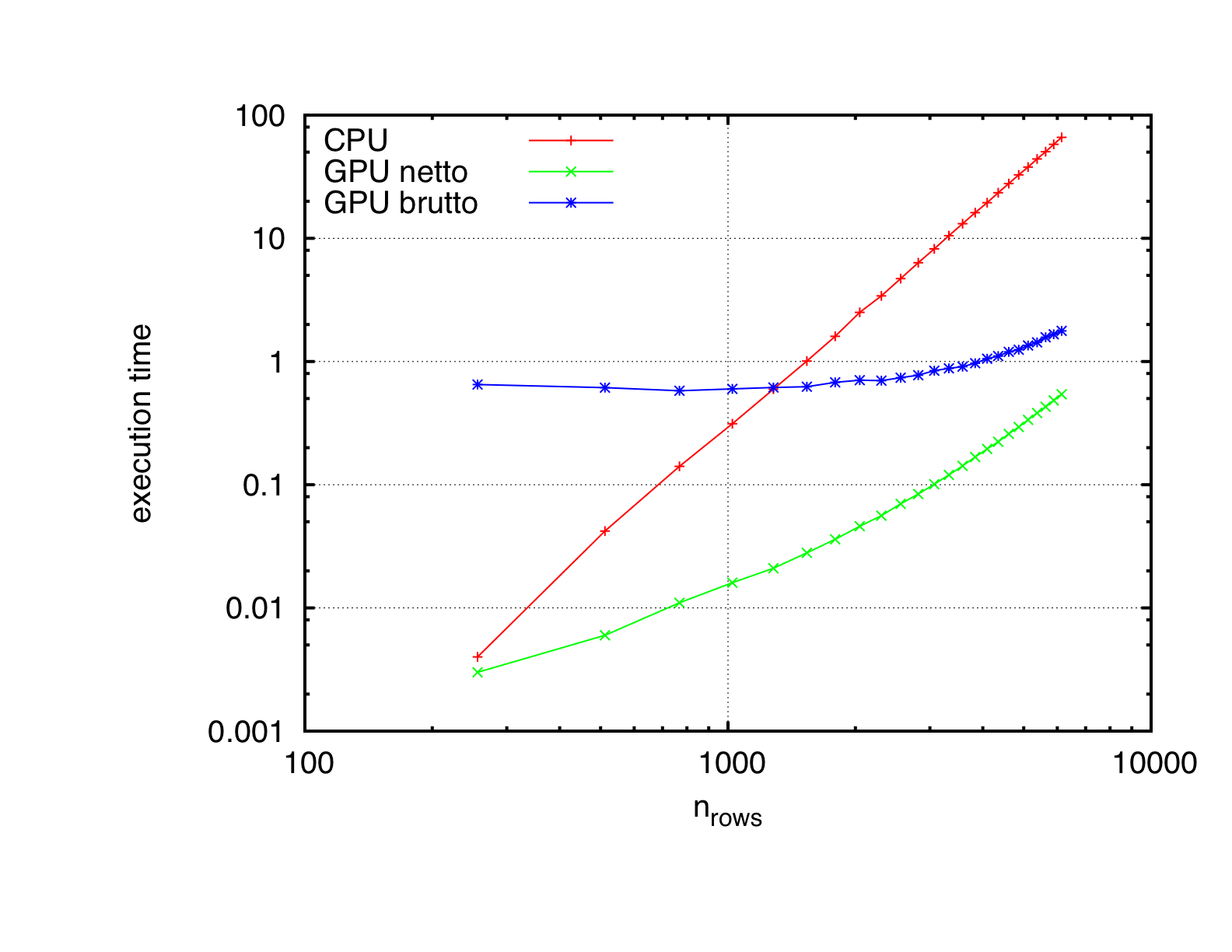
Execution times on quad-core Xeon 2.26 GHz gtx 460

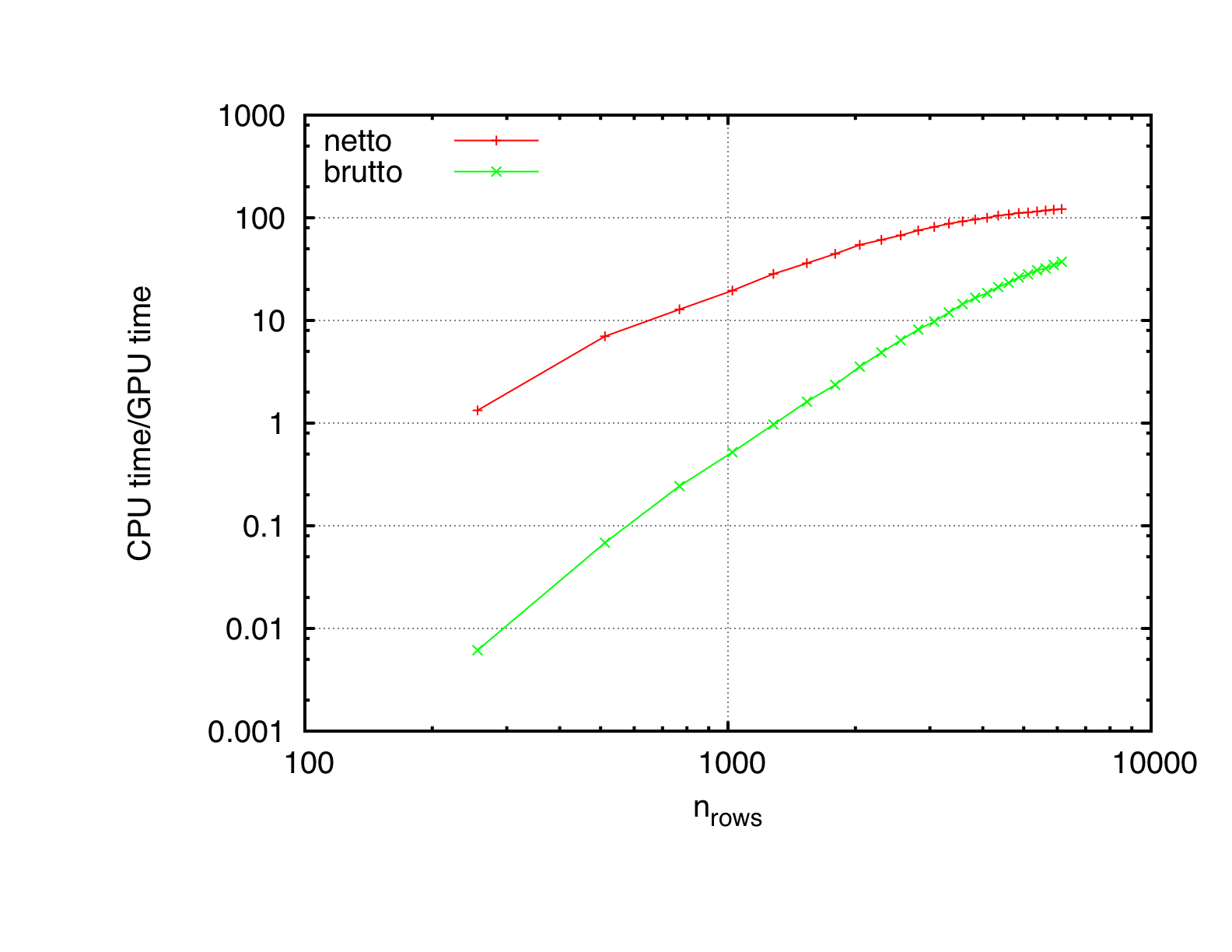
Speedup of GPU over CPU on quad-core Xeon 2.26 GHz gtx 460

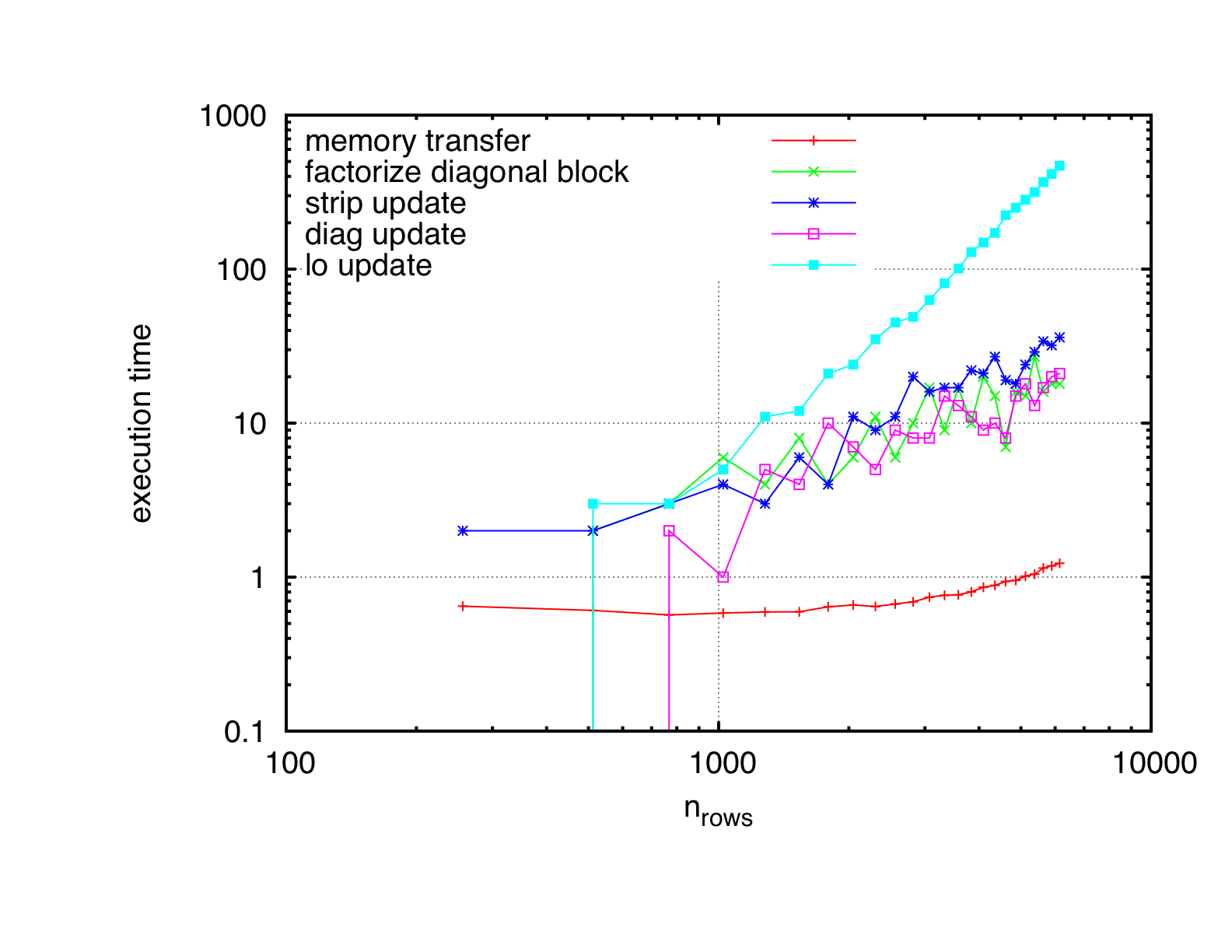
Individual timing of the different kernels of the cholesky factorization on gtx 460

The plain program

(If you are looking at a locally installed CUDA HPC Praktikum version, then the program can be found at .. /.. /testsite / /step-1 /step-cu.cc . Otherwise, this is only the path on some remote server.)

 #ifndef CUDA_KERNEL_STEP_1_CU_H
 #define CUDA_KERNEL_STEP_1_CU_H
 
 
 
 
 
 
 #define TILE_SIZE 16

 void single_thread_cholesky(float * A, int n_rows);
 
 void cholesky(float * A, int n_rows);
 cudaError_t factorize_diagonal_block(float *A,int block_offset, int global_row_length );
 
 void strip_update(float *A, int block_offset, int n_remaining_blocks, int n_rows_padded );
 
 void diag_update(float *A, int block_offset, int global_row_length, int n_remaining_blocks  );
 
 void lo_update(float *A, int block_offset, int n_blocks, int global_row_length, int n_remaining_blocks );
 
 #if __CUDA_ARCH__ >= 130
 void cholesky(double * a_d, int n_rows);
 cudaError_t factorize_diagonal_block(double *A,int block_offset, int global_row_length );
 
 void strip_update(double *A, int block_offset, int n_remaining_blocks, int n_rows_padded ) ;
 
 void diag_update(double *A, int block_offset, int global_row_length, int n_remaining_blocks  );
 
 void lo_update(double *A, int block_offset, int n_blocks, int global_row_length, int n_remaining_blocks );
 #endif
 
 
 
 #endif // CUDA_KERNEL_STEP_1_CU_H
 
 
 
 #include <cutil_inline.h>
 #include <cuda_kernel_wrapper_step-1.cu.h>

 __device__ int lex_index_2D(int r, int c, int row_length)
 {
     return c +  r*row_length;
 }

 __device__ int global_pos(int t_pos, int block_offset)
 {
     return t_pos + TILE_SIZE*block_offset;
 }

 template<typename T>
 __global__
 void
 __single_thread_cholesky(T *A, const int gpu_tile_size)
 {
     for (unsigned int r = 0; r < gpu_tile_size; ++r)
     {
             T sum = 0.;
             unsigned int idx;
             unsigned int idx_c;
             for (unsigned int u = 0; u < r; ++u)
             {
                 idx = lex_index_2D(r, u, gpu_tile_size);
                 sum += A[idx] * A[idx];
             }
             idx = lex_index_2D(r, r, gpu_tile_size);
             A[idx] = sqrt(A[idx] - sum);
 
             for (unsigned int c = r+1; c < gpu_tile_size; ++c)
             {
                     sum = 0.;
 
                     for (unsigned int u = 0; u < r; ++u)
                     {
                         idx_c = lex_index_2D(c, u, gpu_tile_size);
                         idx   = lex_index_2D(r, u, gpu_tile_size);
                         sum += A[idx_c]*A[idx];
                     }
 
                     idx_c = lex_index_2D(c, r, gpu_tile_size);
                     idx   = lex_index_2D(r, c, gpu_tile_size);
                     A[idx_c]  = A[idx] - sum;
 
                     idx   = lex_index_2D(r, r, gpu_tile_size);
                     A[idx_c] /= A[idx];
             }
     }
 }

 template<typename T>
 __global__
 void
 __factorize_diagonal_block(T *A, int block_offset,
                            int global_row_length)
 {
     int col = threadIdx.x;
 
     int row = threadIdx.y;
 
     int global_row = global_pos(row,block_offset);
     int global_col = global_pos(col,block_offset);
     int idx = lex_index_2D(global_row, global_col, global_row_length);
 
     __shared__ T L[TILE_SIZE][TILE_SIZE+1];
 
     L[row][col]= A[idx];
     __syncthreads();
 
     T fac;
 
     for(int k=0;k<TILE_SIZE;k++)
     {
         __syncthreads();
         fac=rsqrtf(L[k][k]);
         __syncthreads();
 
         if ((row==k)&&(col>=k)) L[col][row]=(L[col][row])*fac;
 
         __syncthreads();
 
 
         if ((row>=col)&&(col>k)) L[row][col] -= L[col][k]*L[row][k];
     }
 
     __syncthreads();
 
     if (row>=col) A[idx] = L[row][col];
 }

 template<typename T>
 __global__
 void
 __strip_update(T *A, int block_offset, int global_row_length)
 {
 
     int boffy=block_offset;
     int boffx = blockIdx.x + boffy + 1;
 
     int col = threadIdx.x;
     int row = threadIdx.y;
 
     __shared__ T topleft[TILE_SIZE][TILE_SIZE+1];
     __shared__ T workingmat[TILE_SIZE][TILE_SIZE+1];
 
     int global_row = global_pos(row,block_offset);
     int global_col = global_pos(col,block_offset);
 
     int idx = lex_index_2D(global_row, global_col, global_row_length);
 
     topleft[row][col]=A[idx];
 
     global_row = global_pos(row,boffx);
     int idx_w = lex_index_2D(global_row, global_col, global_row_length);
     workingmat[col][row]= A[idx_w];
 
     __syncthreads();
 
     if(row==0)
         for (int k=0;k<TILE_SIZE;k++)
         {
             T sum=0.;
             for (int m=0;m<k;m++) sum += topleft[k][m]*workingmat[m][col];
 
             workingmat[k][col]=(workingmat[k][col] - sum)/topleft[k][k];
         }
 
     __syncthreads();
 
     A[idx_w] = workingmat[col][row];
 }

 template<typename T>
 __global__
 void
 __diag_update(T *A, int block_offset, int global_row_length)
 {
     int boffx = blockIdx.x + block_offset + 1;
 
     int col = threadIdx.x;
     int row = threadIdx.y;
 
     int global_row = global_pos(row, boffx);
     int global_col = global_pos(col, block_offset);
 
     int idx = lex_index_2D(global_row, global_col, global_row_length);
 
     __shared__ T left[TILE_SIZE][TILE_SIZE+1];
 
     left[row][col]= A[idx];
 
     __syncthreads();
 
     T sum = 0.f;
 
     if(row>=col)
      {
         for(int kk=0; kk<TILE_SIZE; kk++) sum += left[row][kk]*left[col][kk];
 
         global_col = global_pos(col, boffx);
         idx = lex_index_2D(global_row, global_col, global_row_length);
 
         A[idx] -= sum;
      }
 }

 template<typename T>
 __global__
 void
 __lo_update(T *A, int block_offset, int n_blocks, int global_row_length)
 {
 
     int col = threadIdx.x;
     int row = threadIdx.y;
 
     int boffy=blockIdx.y+block_offset+1;
     int boffx=boffy+1;
 
     __shared__ T left[TILE_SIZE][TILE_SIZE];
 
     __shared__ T upt[TILE_SIZE][TILE_SIZE+1];
 
 
     int global_row = global_pos(row, boffy);
     int global_col = global_pos(col, block_offset);
 
     int idx = lex_index_2D(global_row, global_col, global_row_length);
 
     upt[row][col]=A[idx];
 
     for (;boffx<n_blocks;boffx++)
     {
        global_row = global_pos(row, boffx);
        idx = lex_index_2D(global_row, global_col, global_row_length);
 
         left[row][col]=A[idx];
 
         __syncthreads();
 
         T matrixprod=0.f;
 
         for (int kk=0;kk<TILE_SIZE;kk++)
             matrixprod+=left[row][kk]*upt[col][kk];
 
         __syncthreads();
 
         global_col = global_pos(col, boffy);
         idx = lex_index_2D(global_row, global_col, global_row_length);
 
         A[idx]-=matrixprod;
     }
 }

 template<typename T>
 void
 single_thread_cholesky(T * a_d, int n_rows)
 {
     __single_thread_cholesky<<<1,1>>>(a_d, n_rows);
 }

 template<typename T>
 void
 _cholesky(T * a_d, int n_rows)
 {
     cudaError_t error;
 
     int n_blocks = (n_rows+int(TILE_SIZE)-1)/int(TILE_SIZE);
     int n_rows_padded = n_blocks*TILE_SIZE;
 
     dim3 threads(TILE_SIZE,TILE_SIZE);
 
     dim3 logrid;
 
     for(int i=n_blocks; i>2; --i)
     {
         logrid.x=1;
         logrid.y=i-2;
 
         dim3 stripgrid(i-1);
 
         __factorize_diagonal_block<<<1, threads>>>(a_d, n_blocks-i, n_rows_padded);
         cudaThreadSynchronize();
 
         __strip_update<<<stripgrid, threads>>>(a_d, n_blocks-i, n_rows_padded);
         cudaThreadSynchronize();
 
         __diag_update<<<stripgrid, threads>>>(a_d, n_blocks-i, n_rows_padded);
         cudaThreadSynchronize();
         __lo_update<<< logrid, threads >>>(a_d, n_blocks-i, n_blocks, n_rows_padded);
         cudaThreadSynchronize();
     }
 
     if(n_blocks>1)
     {
         __factorize_diagonal_block<<<1, threads>>>(a_d, n_blocks-2,
                                                    n_rows_padded);
         cudaThreadSynchronize();
 
         __strip_update<<<1, threads>>>(a_d, n_blocks-2, n_rows_padded);
         cudaThreadSynchronize();
 
         __diag_update<<<1, threads>>>(a_d, n_blocks-2, n_rows_padded);
         cudaThreadSynchronize();
     }
 
     __factorize_diagonal_block<<<1, threads>>>(a_d, n_blocks-1, n_rows_padded);
 
     cudaThreadSynchronize();
 
     error=cudaGetLastError();
     if (error != cudaSuccess)
     {
        printf("     Error code %d: %s.\n",error,cudaGetErrorString(error));
        exit(-1);
     }
 }
 
 template<typename T>
 cudaError_t
 _factorize_diagonal_block(T * a_d, int block_offset, int n_rows_padded )
 {
     dim3 threads(TILE_SIZE,TILE_SIZE);
     __factorize_diagonal_block<<<1, threads>>>(a_d, block_offset, n_rows_padded);
         cudaThreadSynchronize();
 
            return cudaGetLastError();
 }
 
 
 template<typename T>
 void
  _strip_update(T *a_d, int block_offset , int n_remaining_blocks, int n_rows_padded )
 {
      cudaError_t error;
 
      dim3 stripgrid(n_remaining_blocks-1);
      dim3 threads(TILE_SIZE,TILE_SIZE);
     __strip_update<<<stripgrid, threads>>>(a_d, block_offset, n_rows_padded);
         cudaThreadSynchronize();
     error=cudaGetLastError();
     if (error != cudaSuccess)
     {
        printf("     Error code %d: %s.\n",error,cudaGetErrorString(error));
        exit(-1);
     }
 }
 
 template<typename T>
 void
 _diag_update(T *a_d, int block_offset, int n_rows_padded , int n_remaining_blocks )
 {
      cudaError_t error;
      dim3 stripgrid(n_remaining_blocks-1);
      dim3 threads(TILE_SIZE,TILE_SIZE);
  __diag_update<<<stripgrid, threads>>>(a_d, block_offset, n_rows_padded);
      cudaThreadSynchronize();
  error=cudaGetLastError();
  if (error != cudaSuccess)
  {
     printf("     Error code %d: %s.\n",error,cudaGetErrorString(error));
     exit(-1);
  }
 }
 
 template<typename T>
 void
 _lo_update(T *a_d, int block_offset, int n_blocks, int n_rows_padded, int n_remaining_blocks )
 {
      cudaError_t error;
      dim3 logrid;
      logrid.x=1;
      logrid.y=n_remaining_blocks-2;
      dim3 threads(TILE_SIZE,TILE_SIZE);
     __lo_update<<< logrid, threads >>>(a_d, block_offset, n_blocks, n_rows_padded);
         cudaThreadSynchronize();
     error=cudaGetLastError();
     if (error != cudaSuccess)
     {
        printf("     Error code %d: %s.\n",error,cudaGetErrorString(error));
        exit(-1);
     }
 }
 
 cudaError_t factorize_diagonal_block(float *A,int block_offset, int global_row_length )
 { return _factorize_diagonal_block(A, block_offset, global_row_length  );}
 
 void strip_update(float *A, int block_offset, int n_remaining_blocks, int n_rows_padded )
 {_strip_update(A, block_offset, n_remaining_blocks , n_rows_padded );}
 
 void diag_update(float *A, int block_offset, int global_row_length, int n_remaining_blocks  )
 {_diag_update(A, block_offset, global_row_length, n_remaining_blocks  );}
 
 void lo_update(float *A, int block_offset, int n_blocks, int global_row_length, int n_remaining_blocks )
 {_lo_update(A, block_offset, n_blocks, global_row_length, n_remaining_blocks  );}

 void cholesky(float * a_d, int n_rows) { _cholesky(a_d, n_rows); }
 
 #if __CUDA_ARCH__ >= 130
 void cholesky(double * a_d, int n_rows) { _cholesky(a_d, n_rows); }
 cudaError_t factorize_diagonal_block(double *A,int block_offset, int global_row_length )
 { return _factorize_diagonal_block(A, block_offset, global_row_length  );}
 
 void strip_update(double *A, int block_offset, int n_remaining_blocks, int n_rows_padded )
 {_strip_update(A, block_offset, n_remaining_blocks , n_rows_padded );}
 
 void diag_update(double *A, int block_offset, int global_row_length, int n_remaining_blocks  )
 {_diag_update(A, block_offset, global_row_length, n_remaining_blocks  );}
 
 void lo_update(double *A, int block_offset, int n_blocks, int global_row_length, int n_remaining_blocks )
 {_lo_update(A, block_offset, n_blocks, global_row_length, n_remaining_blocks  );}
 #endif
 
 
 
 #ifndef CUDADriver_STEP_1_H
 #define CUDADriver_STEP_1_H
 
 #include <lac/FullMatrixAccessor.h>
 #include <lac/blas++.h>
 
 #define __CUDA_ARCH__ 130
 
 namespace step1 {

 template<typename T>
 class CUDADriver {
 
 public:
     typedef typename blas_pp<T, cublas>::blas_wrapper_type BW;
     typedef typename blas_pp<T, cublas>::FullMatrixAccessor FullMatrixAccessor;
     typedef typename blas_pp<T, cublas>::Matrix Matrix;
     typedef typename blas_pp<T, cublas>::SubMatrix SubMatrix;
     typedef typename blas_pp<T, cublas>::MatrixSubCol MatrixSubCol;
     typedef typename blas_pp<T, cublas>::Vector Vector;
     typedef typename blas_pp<T, cublas>::SubColVector SubColVector;
     typedef typename blas_pp<T, cublas>::SubVectorBase SubVectorBase;
 
     typedef std::map<std::string,double> TimerName2Value;
 
 
 
     CUDADriver();
 
     ~CUDADriver ();
 
     double factorize(FullMatrixAccessor& A);
 
     double factorize(::FullMatrix<T> &A);
 
     void factorize(FullMatrixAccessor& A, TimerName2Value& times);
 
     void single_thread_cholesky(FullMatrixAccessor& A);
 
 
 private:
     Matrix A_d;
 
 };
 
 } // namespace step1 END
 
 #endif // CUDADriver_STEP_1_H
 
 
 
 #ifndef CUDA_DRIVER_STEP_1_HH
 #define CUDA_DRIVER_STEP_1_HH
 
 #include <base/CUDATimer.h>
 
 #include "cuda_driver_step-1.h"
 
 #include "cuda_kernel_wrapper_step-1.cu.h"
 
 #include <cutil_inline.h>
 
 #include <QTime>

 template<typename T>
 step1::CUDADriver<T>::CUDADriver()
 {
 }

 template<typename T>
 step1::CUDADriver<T>::~CUDADriver()
 {
 }

 template<typename T>
 double
 step1::CUDADriver<T>::factorize(FullMatrixAccessor& A)
 {
     this->A_d = A;
 
     QTime t;
     t.start();
     cholesky(this->A_d.array().val(), this->A_d.n_rows() );
 
     double kernel_time = t.elapsed()/1000.;
 
     A = this->A_d;
 
     return kernel_time;
 }
 
 template<typename T>
 void
 step1::CUDADriver<T>::factorize(FullMatrixAccessor& A, TimerName2Value& times)
 {
     this->A_d = A;
 
     QTime t;
     {
 
 
         int n_blocks = (A.n_rows()+int(TILE_SIZE)-1)/int(TILE_SIZE);
         int n_rows_padded = n_blocks*TILE_SIZE;
 
         T* a_d = this->A_d.array().val();
 
         times["factorize_diagonal_block"] = 0.;
         times["strip_update"] = 0.;
         times["diag_update"] = 0.;
         times["lo_update"] = 0.;
 
         for(int i=n_blocks; i>2; --i)
         {
             t.restart();
             cudaError_t error = factorize_diagonal_block(a_d, n_blocks-i, n_rows_padded);
             times["factorize_diagonal_block"]+=t.elapsed();
 
             AssertThrow(error == cudaSuccess, ::ExcMessage( cudaGetErrorString(error) ) );
 
 
             t.restart();
             strip_update(a_d, n_blocks-i, i , n_rows_padded);
             times["strip_update"]+=t.elapsed();
 
             t.restart();
             diag_update(a_d, n_blocks-i, n_rows_padded, i);
             times["diag_update"]+=t.elapsed();
 
             t.restart();
             lo_update(a_d, n_blocks-i, n_blocks, n_rows_padded,i);
             times["lo_update"]+=t.elapsed();
         }
 
         if(n_blocks>1)
         {
             factorize_diagonal_block(a_d, n_blocks-2, n_rows_padded);
 
             strip_update(a_d, n_blocks-2, 2, n_rows_padded);
 
             diag_update(a_d, n_blocks-2, n_rows_padded,  2);
         }
 
         factorize_diagonal_block(a_d, n_blocks-1, n_rows_padded);
 
     }
 
 
 
 
     A = this->A_d;
 
 }

 template<typename T>
 void
 step1::CUDADriver<T>::single_thread_cholesky(FullMatrixAccessor& A)
 {
     this->A_d = A;
 
     single_thread_cholesky(this->A_d.array().val(), this->A_d.n_rows() );
 
     A = this->A_d;
 }
 
 #endif // CUDA_DRIVER_STEP_1_HH
 
 
 
 #include <iostream>
 #include <vector>
 
 #include <QThread>
 #include <QTime>
 
 #include <base/convergence_table.h>
 #include <lac/full_matrix.h>
 
 
 #include "cuda_driver_step-1.h"
 #include "cuda_driver_step-1.hh"
 
 #include <lac/FullMatrixAccessor.h>
 #include <lac/MatrixCreator.h>
 
 namespace step1 {

 template<typename Number>
 class CholeskyTest : public QThread
 {
     static const unsigned int max_display_size = 20;
 
 public:
 
     CholeskyTest(int n_r, ::ConvergenceTable& s_table);
 
 protected:
 
     void setup_and_assemble_test_matrix();
 
     void factorize();
 
     void check_results();
 
     void run();
 
     int n_rows;
 
     ::ConvergenceTable & speedup_table;
 
     ::FullMatrix<Number> A, L, L_T;
 
 };

 class Cholesky {
 
 
 
 public:
     template<typename T> static void cpu(std::vector<std::vector<T> > & A);
 
     template<typename T/ *, int tile_size* /> static void cpu_tiled(T* A, int tile_size);
 
     template<typename T> static void LLtMult(T * A, const T * L, int n_rows);
 };

 template<typename Number>
 CholeskyTest<Number>::CholeskyTest(int n_r, ::ConvergenceTable& s_table)
 :
     n_rows(n_r),
     speedup_table(s_table)
 {}

 template<typename Number>
 void CholeskyTest<Number>::setup_and_assemble_test_matrix()
 {
     this->A.reinit(n_rows, n_rows);
     this->L.reinit(n_rows, n_rows);
     this->L_T.reinit(n_rows, n_rows);
 
     QTime t;
 
     this->speedup_table.add_value("n rows", n_rows);
 
     std::cout << "Initial Cholesky factor deal.II :" << std::endl;
     std::cout << "----------------------------------------------------"
               << std::endl;
 #ifdef nUSE_HADAMARD
     t.start();
 
     for (unsigned int r = 0; r < n_rows; ++r)
         for (unsigned int c = r; c <n_rows; ++c)
             L(r,c) = 1e-0*(r+2)*(c+2);
     qDebug("Time for CPU-based setup of Cholesky factor : %f s",
            t.elapsed()/1000.);
 
     if ( L.n_rows() < max_display_size)
         L.print(std::cout, 10, 5);
     if ( L.n_rows() < max_display_size)
         std::cout << std::endl;std::cout << std::endl;
 
     {
         t.restart();
         L_T.copy_from(L);
         qDebug("Time for CPU-based copying of Cholesky factor : %f s",
                t.elapsed()/1000.);
 
         t.restart();
         L_T.Tmmult(A, L, false);
         qDebug("Time for CPU-based multiplication of Cholesky factor"
                " : %f s",
                t.elapsed()/1000.);
         L_T.copy_from(A);
     }
     std::cout << "Matrix to factorize :" << std::endl;
     std::cout << "----------------------------------------------------"
             << std::endl;
     if ( A.n_rows() < max_display_size)
         A.print(std::cout, 10, 5);
     if ( A.n_rows() < max_display_size)
         std::cout << std::endl;std::cout << std::endl;
 #else
     MatrixCreator::extended_hadamard(n_rows, A);
 #endif
 
 }

 template<typename Number>
 void CholeskyTest<Number>::run()
 {
     this->setup_and_assemble_test_matrix();
 
     QTime t;
 double cpu_time, gpu_time;
 
     t.restart();
     {
         FullMatrixAccessor<Number> A_h(A);
         Cholesky::cpu_tiled<Number>(A_h.val(), A_h.n_rows() );
     }
 
     cpu_time =  t.elapsed()/1000.;
     qDebug("Time for CPU-based Cholesky factorization : %f s",
            cpu_time);
 
     this->speedup_table.add_value("CPU factorization", cpu_time);
     this->speedup_table.set_precision("CPU factorization", 10);
 
 
     std::cout << "CPU-factorized Matrix (lower triangle contains "
             << "transposed Cholesky factor) :" << std::endl;
     std::cout << "----------------------------------------------------"
             << std::endl;
     if ( A.n_rows() < max_display_size)
     A.print(std::cout, 10, 5);
 
 
     std::cout << "Matrix to factorize on GPU :" << std::endl;
     std::cout << "----------------------------------------------------"
             << std::endl;
     if ( A.n_rows() < max_display_size)
     A.print(std::cout, 10, 5);
     std::cout << std::endl;std::cout << std::endl;
 
     Assert( A.n_rows() == A.n_cols(),
            ::ExcMessage("Matrix not square! Cholesky impossible"));
 
 
     double kernel_time = 0;
 
     CUDADriver<Number> run;
     t.restart();
     {
         FullMatrixAccessor<Number> A_h(A, true);
         kernel_time = run.factorize(A_h);
     }
     gpu_time =  t.elapsed()/1000.;
 
     qDebug("Time for GPU-based Cholesky factorization %f"
            " including data transfer : %f s\n"
            "speed up factor factorization : %f netto : %f n_rows : %d\n",
             kernel_time,
             gpu_time,
             cpu_time/kernel_time,
             cpu_time/gpu_time,
             n_rows);
 
     this->speedup_table.add_value("pure GPU fac", kernel_time);
     this->speedup_table.set_precision("pure GPU fac", 10);
 
     this->speedup_table.add_value("GPU fac incl data transfer", gpu_time);
     this->speedup_table.set_precision("GPU fac incl data transfer", 10);
 
 
     std::cout << "GPU-factorized Matrix (lower triangle contains "
               << "transposed Cholesky factor) :" << std::endl;
     std::cout << "----------------------------------------------------"
             << std::endl;
     if ( A.n_rows() < max_display_size)
         A.print(std::cout, 10, 5);
 
 
     typename CUDADriver<Number>::TimerName2Value times;
     {
         FullMatrixAccessor<Number> A_h(A, true);
         run.factorize(A_h, times);
     }
 
 
     typename CUDADriver<Number>::TimerName2Value::const_iterator e=times.begin(), end_t=times.end();
     for( ; e != end_t ; ++e) {
 
         this->speedup_table.add_value(e->first, e->second);
         this->speedup_table.set_precision(e->first,10);
     }
 
 
     return;
 }

 template<typename T>
 void Cholesky::cpu_tiled(T* A, int tile_size)
 {
 
         for (unsigned int r = 0; r < tile_size; ++r)
         {
                 T sum = 0.;
                 unsigned int idx;
                 unsigned int idx_c;
 
                 for (unsigned int u = 0; u < r; ++u)
                 {
                     idx = r*tile_size + u;
                     sum += A[idx] * A[idx];
                 }
                 idx = r*tile_size + r;
                 A[idx] = sqrt(A[idx] - sum);
 
                 for (unsigned int c = r+1; c < tile_size; ++c)
                 {
                         T tmp = 0.;
 
                         for (unsigned int u = 0; u < r; ++u)
                         {
                             idx_c = c*tile_size + u;
                             idx   = r*tile_size + u;
                             tmp += A[idx_c]*A[idx];
                         }
 
                         idx_c = c*tile_size + r;
                         idx   = r*tile_size + c;
                         A[idx_c]  = A[idx] - tmp;
                         A[idx_c] /= A[r*tile_size + r];
 
                 }
         }
 }

 template<typename T>
 void Cholesky::LLtMult(T * A, const T * L, int n_rows)
 {
     for (unsigned int r = 0; r < n_rows; ++r)
         for (unsigned int c = 0; c <=r; ++c)
         {
             unsigned int idx = c + (r*(r+1))/2;
             unsigned int k_max = std::min(r,c);
 
             A[idx] = 0.;
 
             for (unsigned int k = 0; k < k_max; ++k)
             {
                 unsigned int idx_k   = k + (r*(r+1))/2;
                 unsigned int idx_k_T = k + (c*(c+1))/2;
                 A[idx] += L[idx_k]*L[idx_k_T];
             }
         }
 
 }

 template<typename Number>
 class MyFancySimulation {
 
 public:
 
     MyFancySimulation() {}
 
     void run();
 
     static std::string precision_id();
 
 };

 template<>
 std::string MyFancySimulation<float>::precision_id()
 {
     return "float";
 }
 
 template<>
 std::string MyFancySimulation<double>::precision_id()
 {
     return "double";
 }
 
 
 
 }

 template<typename Number>
 void step1::MyFancySimulation<Number>::run()
 {   
     for (int n_min = 256; n_min < 513; n_min+=1024)
     {
         ::ConvergenceTable factorization_times;
 
         for (int n = n_min; n < n_min+768; n+=256)
         {
             CholeskyTest<Number> driver(n, factorization_times);
 
             driver.start();
             driver.wait();
 
         }
 
         std::ostringstream filename;
 
         filename << "chol_fac_times_" << n_min << "_" << precision_id().c_str() << ".dat";
 
         std::ofstream out(filename.str().c_str());
 
         factorization_times.write_text(out);
     }
 
 
     std::cout << "Fertig." << std::endl;
 }

 int main(int / *argc* /, char * / *argv* /[])
 {
 
     using namespace step1;
 
     MyFancySimulation<float> machma_float;
 
     machma_float.run();
 
 
     MyFancySimulation<double> machma_double;
 
     machma_double.run();
 
 }

CUDA Lab Course Reference Manual 2011

The step-1 tutorial program

Introduction

Cholesky Factorization

Algorithm

Special requirements due to CUDA

Literatur

The commented program

Declarations of kernel wrapper functions

Device Functions

Device Function: lex_index_2D

Device Function: global_pos

Kernel

Kernel: __single_thread_cholesky

Parallelization of Cholesky Factorization

Kernel: factorize_diagonal_block

Kernel: strip_update

Kernel: diag_update

Kernel: lo_update

Function: single_thread_cholesky

Function: cholesky_impl

Function: cholesky

Class: CUDADriver

Constructor: CUDADriver

Destructor: ~CUDADriver

Function: factorize

Function: single_thread_cholesky

Class: CholeskyTest

Klasse: Cholesky

Constructor: CholeskyTest

Function: setup_and_assemble_test_matrix

Function: run

Function: cpu_tiled

Function: LLtMult

class: MyFancySimulation

Function: precision_id

Function: run

Funktion: main

Results

The plain program