The step-11 tutorial program
Introduction
This project invetigates the possibilities to study homogeneously decaying turbulence with CUDA.
Motivation
The incompressible Navier-Stokes equation read:
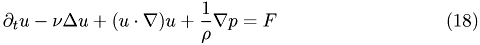
together with

where 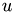 denotes the velocity field,
denotes the velocity field, 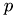 the pressure and
the pressure and 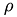 the density of the fluid.
the density of the fluid.
By defining

we obtain the so called vorticity equation
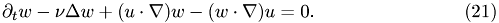
In 2 space dimensions we have
The general-purposed PDE solver from packages such as deal.II are often overkill for academic problems (such as simple geometries and boundary conditions) and therefore there is interest in a more specialized approach. 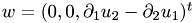 and therefore
and therefore 
If we assume periodic boundary conditions on the domain
![$[0,2\pi]^2$](form_45.png) , it is convenient to expand
, it is convenient to expand 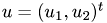 and
and 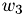 into their corresponding Fourier series:
into their corresponding Fourier series: 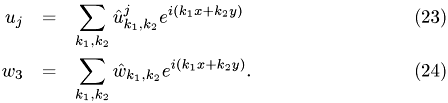
Eq. {eq:div_u} and {eq:def_w} then give
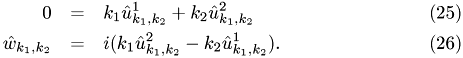
We can solve these equations and obtain {Of course
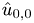 can not be fixed by
can not be fixed by 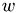 , but this term is not even fixed by {eq:ns_gl}.}
, but this term is not even fixed by {eq:ns_gl}.} 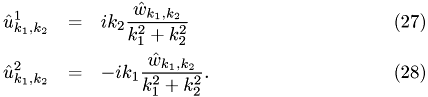
To insert the expansion of
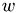 into {eq:w_gl}, we calculate the nonlinear term:
into {eq:w_gl}, we calculate the nonlinear term: 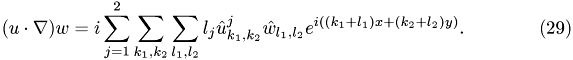
Finally, we obtain the ODE governing the time evolution of the
This is a (huge) coupled system of non-linear ODEs. The nonlinear term is in fact a convolution and can be efficiently evaluated by use of the fast Fourier transform (FFT) and the formula
This results in a complexity of 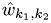 by inserting everything into {eq:w_gl}:
by inserting everything into {eq:w_gl}: 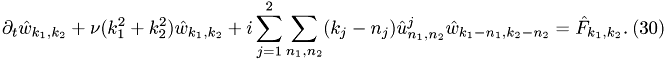
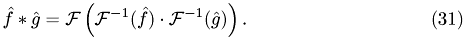
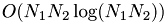 instead of
instead of 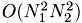 for the naive implementation.
for the naive implementation.
The caveat, as previous work by {zudrop_master} suggests, is that this treatment is prone to rounding errors.
To get rid of the nonlinear term but maintain an at leats partially realistic model, one may consider the 2-dimensional Oseen problem:
where 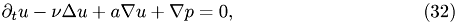
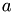 is a known and divergence-free periodic vector field.
is a known and divergence-free periodic vector field.
A highly optimized FFT implementation is already available in the form of the CuFFT library. FFT is mainly needed to evaluate the convolution terms in the resulting ODE system.
Eq. {eq:ODE} and the corresponding equations for {eq:burger} and {eq:oseen} result in huge, highly coupled and (except for {eq:oseen}) nonlinear ODE systems. We will try to speed up the integration of these equation by deploying CUDA at different levels. It may not be suitable to implement a complete ODE solver on the GPU but to only direct the linear algebra parts of the algorithm to CUDA.
To prevent bounding errors from propagating we will probably use a Crank-Nicolson scheme with an implicit Euler step inserted every 10th or so iteration. The commented program
#ifndef CPU_DRIVER_STEP11_H
#define CPU_DRIVER_STEP11_H
namespace step11 {
#include "cuda_driver_tools_step-11.h"
This class organizes the simulation with CPU.
class CPUDriver {
public:
typedef ::Vector<std::complex<double> > MyVector;
typedef ::FullMatrix<std::complex<double> > MyMatrix;
typedef ::Vector<double> RKVector;
CPUDriver() {
timer=0;
}
~CPUDriver ();
void init(int _N, int _n, double _nu, int _solver, double _dt, std::vector<std::complex<double> > &__init_val, std::vector<std::complex<double> > &_aX, std::vector<std::complex<double> > &_aY, std::vector<std::complex<double> > &_RHside);
void run(double T);
void fetch(std::vector<std::complex<double> > &result);
void EulerStep(MyVector &old_val);
void ImplEulerStep(MyVector &old_val);
void TrapezoidalStep(MyVector &old_val);
void RungeKuttaStep(MyVector &old_val, int stage);
void ODESolve(double T, MyVector &old_val, MyVector &new_val, int solver);
void CalcEntry(double _t, double eta, double lambda, MyVector &dest, MyVector &src, bool nondiag);
void GaussSeidel(double _t, double lambda, MyVector &result, MyVector &y, int iterations);
double used_time;
private:
MyVector tmp_val;
MyVector init_val;
MyVector new_val;
MyVector aX;
MyVector aY;
MyVector RHside;
MyVector RHside_tmp;
int N;
int n;
double nu;
int solver;
unsigned int timer;
double dt;
double t;
};
}//end of namespace
#endif // CPU_DRIVER_STEP11_H
#ifndef CPU_DRIVER_STEP_11_HH
#define CPU_DRIVER_STEP_11_HH
#include "cpu_driver_step-11.h"
#include "tools_step-11.h"
step11::CPUDriver::~CPUDriver()
{
if (timer) {
Delete the timer
CUT_SAFE_CALL(cutDeleteTimer(timer));
}
}
This function initializes the needed private variables of the class.
_N : number of Fourier modes _n : number of Fourier modes used in convolution _nu : viscosity _solver,: choose the solver used (explicit Euler, trapezoidal, Runge-Kutta4) dt : time step _init_val : initial values _a,: known vector field a in momentum space _RHside,: right hand side in momentum space void step11::CPUDriver::init(int _N, int _n, double _nu, int _solver, double _dt, std::vector<std::complex<double> > &_init_val, std::vector<std::complex<double> > &_aX, std::vector<std::complex<double> > &_aY, std::vector<std::complex<double> > &_RHside) {
unsigned int k;
N=_N;
n=_n;
nu=_nu;
dt=_dt;
solver=_solver;
t=0.0;
used_time=0.0;
init_val.reinit((2*N+1)*(2*N+1));
new_val.reinit((2*N+1)*(2*N+1));
tmp_val.reinit((2*N+1)*(2*N+1));
aX.reinit((2*N+1)*(2*N+1),false);
aY.reinit((2*N+1)*(2*N+1),false);
RHside.reinit((2*N+1)*(2*N+1),false);
RHside_tmp.reinit((2*N+1)*(2*N+1),false);
for (k=0; k<init_val.size(); k++) {
init_val(k)=_init_val[k];
}
for (k=0; k<aX.size(); k++) {
aX(k)=_aX[k];
aY(k)=_aY[k];
}
for (k=0; k<RHside.size(); k++) {
RHside(k)=_RHside[k];
}
new_val=init_val;
if (timer) {
Delete the timer
CUT_SAFE_CALL(cutDeleteTimer(timer));
}
Create timer.
CUT_SAFE_CALL(cutCreateTimer(&timer));
}
This function calls the ODE-solver and simulates until time t+T.
T : simulation time void step11::CPUDriver::run(double T) {
Start timer.
CUT_SAFE_CALL(cutStartTimer(timer));
Call to ODE solver.
ODESolve(t+T,new_val,new_val,solver);
Stop timer and print passed time.
CUT_SAFE_CALL(cutStopTimer(timer));
printf( "Processing time: %f (ms)\n", cutGetTimerValue(timer));
used_time=cutGetTimerValue(timer);
std::cout << new_val(hGetVecPos(1,2,N)) << std::endl;
}
This function transforms the dealii-vector new_val into a vector of type std::vector<std::complex<double> >.
result : transformed vector void step11::CPUDriver::fetch(std::vector<std::complex<double> > &result) {
assert(aX.size()==new_val.size());
unsigned int k;
for (k=0; k<new_val.size(); k++){
result[k]=new_val(k);
}
}
This function performs a single explicit Euler-step at time t.
Consider an ODE of the form
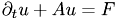 . Then an Euler step performs the following:
. Then an Euler step performs the following: 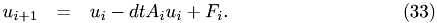
old_val : value calculated in previous step void step11::CPUDriver::EulerStep(MyVector &old_val) {
calculates 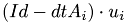
CalcEntry(t,1.0,dt,tmp_val,old_val,false);
add right hand side (at time t)
RHside_tmp = RHside;
RHside_tmp*=hRHsideTime(t);
tmp_val.add(dt, RHside_tmp);
old_val=tmp_val;
}
This function performs a single implicit Euler step at time t. For the ODE
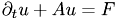 we have
we have 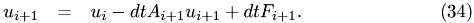
old_val : value calculated in previous step void step11::CPUDriver::ImplEulerStep(MyVector &old_val) {
Calculate the right hand side of the linear system: 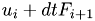 .
.
RHside_tmp = RHside;
RHside_tmp*=(dt*hRHsideTime(t+dt));
RHside_tmp+=old_val;
Solve linear system using Gauss Seidel-iterations.
GaussSeidel(t+dt,-dt,old_val,RHside_tmp,3);
}
This function performs a single step via trapezoidal rule at time t.
For the ODE
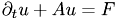 we have
we have 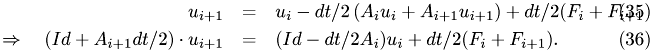
old_val : value calculated in previous step void step11::CPUDriver::TrapezoidalStep(MyVector &old_val) {
Calculate the right hand side of the linear system. First: Calculate 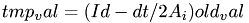 :
:
CalcEntry(t,1.0,dt/2,tmp_val,old_val,false);
Second: tmp_val += dt/2*(RHside_{i+1} + RHside_i):
RHside_tmp = RHside;
RHside_tmp*=hRHsideTime(t);
tmp_val.add(dt/2.0, RHside_tmp);
RHside_tmp = RHside;
RHside_tmp*=hRHsideTime(t+dt);
tmp_val.add(dt/2.0, RHside_tmp);
Solve linear system using Gauss Seidel-iterations.
GaussSeidel(t+dt,-dt/2,old_val,tmp_val,3);
}
This function performs a single Runge-Kutta step at time t.
For the ODE
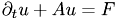 we have
we have 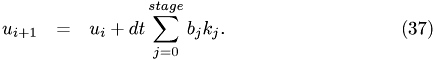
old_val : value calculated in previous step stage : stage of Runge-Kutta algorithm void step11::CPUDriver::RungeKuttaStep(MyVector &old_val, int stage) {
int size= old_val.size();
MyVector k(size*stage);
int i, m, entry;
MyVector sum(size);
Calculate 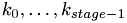 .
.
for (i=0; i<stage; i++) {
sum.reinit(size);
Calculate 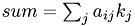 .
.
for (entry=0; entry<size; entry++) {
for (m=0; m<i; m++) {
sum(entry) += getRK_A(i,m,stage)*k(m*size+entry);
}
}
Use position 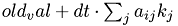 .
.
sum*=dt;
sum+=old_val;
Insert time t+c(i)dt and position 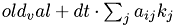 .
.
CalcEntry(t+dt*getRK_c(i,stage), 0.0, 1.0, tmp_val, sum, false);
RHside_tmp = RHside;
RHside_tmp*=hRHsideTime(t+dt*getRK_c(i,stage));
tmp_val+=RHside_tmp;
Write result to k.
for (entry=0; entry<size; entry++) {
k(i*size+entry)=tmp_val(entry);
}
}
k.print(); Calculate 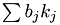 .
.
MyVector bTIMESk;
bTIMESk.reinit(size);
for (i=0; i<size; i++) {
for (m=0; m<stage; m++) {
bTIMESk(i) += k(m*size+i)*getRK_b(m,stage);
}
}
Update value: 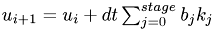 .
.
bTIMESk *= dt;
old_val+=bTIMESk;
}
This is the ODE solver implemented on the CPU.
T : simulation time old_val : initial value new_val : result after time evolution T solver : choose ODE-solver void step11::CPUDriver::ODESolve(double T, MyVector &old_val, MyVector &new_val, int solver) {
std::cout << "CPU-ODE-Solver v. 0.5 (Codename Komsomol): dt=" << dt << ", T=" << T << std::endl;
new_val=old_val;
while (t<T) {
switch (solver) {
case ODE_EULER:
EulerStep(new_val);
break;
case ODE_TRAP:
TrapezoidalStep(new_val);
break;
case ODE_RK:
RungeKuttaStep(new_val, 4);
break;
case ODE_IMPL_EULER:
ImplEulerStep(new_val);
break;
/ * case ODE_TRAP_STABLE:
if ( count_t==200 ) {
hImplEulerStep(dt,A,new_val);
count_t=0;
}
else {
hTrapezoidalStep(t,dt,new_val);
count_t++;
}
break;
* /
}
t+=dt;
}
}
This function calculates the matrix vector product 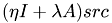 . If nondiag is specified, the product lambda*(A-D)src is calculated, where A-D is A without its diagonal entries.
. If nondiag is specified, the product lambda*(A-D)src is calculated, where A-D is A without its diagonal entries.
_t,: time eta,: 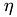
lambda : 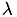
dest : resulting vector src : input vector nondiag : if specified, use diagonal-free matrix void step11::CPUDriver::CalcEntry(double _t, double eta, double lambda, MyVector &dest, MyVector &src, bool nondiag) {
int n1,n2,k1,k2;
int max_n1,min_n1,max_n2,min_n2;
std::complex<double> sum;
int pos1,pos2;
MyVector x_tmp((2*N+1)*(2*N+1));
for (k1=-N; k1<=N; k1++) {
max_n1=std::min(k1+N,n);
min_n1=std::max(k1-N,-n);
for (k2=-N; k2<=N; k2++) {
sum=0.0;
We have to make sure that no out-of-bounds accesses occur.
max_n2=std::min(k2+N,n);
min_n2=std::max(k2-N,-n);
for (n1=min_n1; n1<=max_n1; n1++) {
Use helper variable to keep track of position in the array.
pos1=hGetVecPos(n1,min_n2,N);
pos2=hGetVecPos(k1-n1,k2-min_n2,N);
Calculate the convolution with 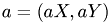 .
.
for (n2=min_n2; n2<=max_n2; n2++) {
sum-=((double)(k1-n1)*aX(pos1)+(double)(k2-n2)*aY(pos1))*src(pos2); hardcode the above formula to gain approximately 20% performance TODO: maybe Gauss' algorithm is even more efficient
sum-=std::complex<double>( ((k1-n1)*std::real(aX(pos1))+(k2-n2)*std::real(aY(pos1)))*std::real(src(pos2))-((k1-n1)*std::imag(aX(pos1))+(k2-n2)*std::imag(aY(pos1)))*std::imag(src(pos2)),((k1-n1)*std::real(aX(pos1))+(k2-n2)*std::real(aY(pos1)))*std::imag(src(pos2))+((k1-n1)*std::imag(aX(pos1))+(k2-n2)*std::imag(aY(pos1)))*std::real(src(pos2)) );
pos1++;
pos2--;
}
}
Multiply by 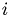 and the time-dependence of
and the time-dependence of 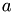 .
.
sum*=(std::complex<double>(0.0,1.0)*hATime(_t));
if (!nondiag) {
Add the diagonal entry (only term that contains no convolution).
sum-=nu*(k1*k1+k2*k2)*src(hGetVecPos(k1,k2,N));
Insert result into the forumla (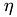 I+
I+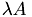 )src.
)src.
x_tmp(hGetVecPos(k1,k2,N)) = eta*src(hGetVecPos(k1,k2,N))+lambda*sum;
}
else {
For GaussSeidel do NOT add the diagonal entry (i.e. n1=0, n2=0) to sum (so do reverse operation).
sum+=std::complex<double>(0.0,1.0)* ((double)k1*aX(hGetVecPos(0,0,N))+(double)k2*aY(hGetVecPos(0,0,N))) * src(hGetVecPos(k1,k2,N)) * hATime(_t);
I is diagonal, so ignore Identity matrix in this case.
x_tmp(hGetVecPos(k1,k2,N)) = lambda*sum;
}
}
}
dest=x_tmp;
}
This is an iterative solver for linear systems. This function implements the Gauss-Seidel algorithm. It assumes the linear system to be of the form
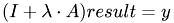 . One iteration performs the following:
. One iteration performs the following: 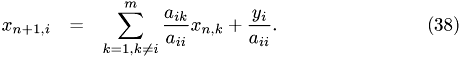
lambda : 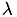
y : right hand side result : resulting vector (solution) iterations : number of iterations void step11::CPUDriver::GaussSeidel(double _t, double lambda, MyVector &result, MyVector &y, int iterations) {
unsigned int size=y.size();
assert(result.size()==size);
assert(size==(unsigned int)(2*N+1)*(2*N+1));
MyVector x_tmp((2*N+1)*(2*N+1));
std::complex<double> tmp;
Choose starting point 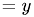 .
.
result=y;
for (int k=0; k<iterations; k++) {
CalcEntry(_t,1.0,lambda,x_tmp,result,true);
result=y;
result-=x_tmp;
int pos=0;
for (int k1=-N; k1<=N; k1++) {
for (int k2=-N; k2<=N; k2++) {
tmp=nu*(k1*k1+k2*k2)+std::complex<double>(0.0,1.0)* ((double)k1*aX(hGetVecPos(0,0,N))+(double)k2*aY(hGetVecPos(0,0,N))) * hATime(_t);
result(hGetVecPos(k1,k2,N))/=(1.0-lambda*tmp);
pos++;
}
}
}
}
#endif
#ifndef CUDADriver_STEP_11_H
#define CUDADriver_STEP_11_H
#include <lac/blas++.h>
#include <string>
namespace step11 {
#include "cuda_driver_tools_step-11.h"
typedef blas_pp<ComplexNumber, cublas>::Vector FFTVectorBase;
class FFTVector : public FFTVectorBase {
public:
typedef FFTVectorBase Base;
FFTVector() {}
FFTVector(int nElements) : Base(nElements) {}
void print();
void setVal(int k, double x, double y) {
ComplexNumber tmp;
tmp.x=x;
tmp.y=y;
set(k,tmp);
}
void zeroVec();
};
This class organizes the simulation with GPU.
class CUDADriver {
public:
typedef FFTVector MyVector;
CUDADriver() {
timer=0;
}
~CUDADriver ();
void init(int _N, int n, double _nu, int _solver, double _dt, std::vector<std::complex<double> > &_init_val, std::vector<std::complex<double> > &_aX, std::vector<std::complex<double> > &_aY, std::vector<std::complex<double> > &_RHside);
void run(double T);
void fetch(std::vector<std::complex<double> > &_result);
void EulerStep(MyVector &old_val);
void ImplEulerStep(MyVector &old_val);
void TrapezoidalStep(MyVector &old_val);
void RungeKuttaStep(MyVector &old_val, int stage);
void ODESolve(double T, MyVector &old_val, MyVector &new_val, int solver);
void dCalcMatProd(MyVector &result, MyVector &rhs, double lambda, double eta, double t, bool nondiag=false);
void dSolveGS(FFTVector &result, MyVector &rhs, double lambda, double t, int iterations);
void testFFT();
ComplexNumber *d_A; ComplexNumber *d_RHside;
double used_time;
private:
MyVector tmp_val;
MyVector init_val;
MyVector new_val;
MyVector aX;
MyVector aY;
MyVector RHside;
MyVector RHside_tmp;
MyVector RK_k;
MyVector sum;
unsigned int timer;
double t;
int N;
double nu;
double dt;
int solver;
};
} // namespace step11 END
#endif // CUDADriver_STEP_11_H
#ifndef CUDA_DRIVER_STEP_11_HH
#define CUDA_DRIVER_STEP_11_HH
#include "cuda_driver_step-11.h"
Deklarationen der kernel-wrapper-Funktionen.
#include "cuda_kernel_wrapper_step-11.cu.h"
#include "tools_step-11.h"
#include <cutil_inline.h>
#include <fstream>
#include <cufft.h>
void step11::FFTVector::print() {
std::vector<ComplexNumber> tmp(this->__n);
ComplexNumber * dst_ptr = &tmp[0];
const ComplexNumber * src_ptr = this->val();
blas_wrapper_type::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
for (int i = 0; i < this->__n; ++i)
std::cout << "(" << tmp[i].x << "," << tmp[i].y << ")" << std::endl;
}
This function sets all entries of a FFTVector to Zero.
void step11::FFTVector::zeroVec() {
for (int i = 0; i < this->__n; i++) {
this->setVal(i,0.0,0.0);
}
}
step11::CUDADriver::~CUDADriver()
{
if (timer) {
Delete the timer
CUT_SAFE_CALL(cutDeleteTimer(timer));
}
}
This function initializes the needed private variables of the class.
_N : number of Fourier modes _n : number of Fourier modes used in convolution _nu : viscosity _solver,: choose the solver used (explicit Euler, trapezoidal, Runge-Kutta4) dt : time step _init_val : initial values _a=(_aX,_aY),: known vector field a in momentum space _RHside,: right hand side in momentum space void step11::CUDADriver::init(int _N, int n, double _nu, int _solver, double _dt, std::vector<std::complex<double> > &_init_val, std::vector<std::complex<double> > &_aX, std::vector<std::complex<double> > &_aY, std::vector<std::complex<double> > &_RHside)
{
int k;
N=_N;
nu=_nu;
solver=_solver;
dt=_dt;
t=0.0;
used_time=0.0;
setParams(N,n,nu);
int size=(2*N+1)*(2*N+1)*sizeof(ComplexNumber);
init_val.reinit((2*N+1)*(2*N+1));
new_val.reinit((2*N+1)*(2*N+1));
tmp_val.reinit((2*N+1)*(2*N+1));
aX.reinit((2*N+1)*(2*N+1));
aX.zeroVec();
aY.reinit((2*N+1)*(2*N+1));
aY.zeroVec();
RHside.reinit((2*N+1)*(2*N+1));
RHside.zeroVec();
RK_k.reinit((2*N+1)*(2*N+1)*4);
sum.reinit((2*N+1)*(2*N+1));
for (k=0; k<init_val.size(); k++) {
init_val.setVal(k,std::real(_init_val[k]), std::imag(_init_val[k]));
}
for (k=0; k<aX.size(); k++) {
aX.setVal(k, std::real(_aX[k]), std::imag(_aX[k]));
aY.setVal(k, std::real(_aY[k]), std::imag(_aY[k]));
}
for (k=0; k<RHside.size(); k++) {
RHside.setVal(k, std::real(_RHside[k]), std::imag(_RHside[k]));
}
Set initial conditions.
new_val=init_val;
if (timer) {
Delete the timer
CUT_SAFE_CALL(cutDeleteTimer(timer));
}
Create timer.
CUT_SAFE_CALL(cutCreateTimer(&timer));
}
This function calls the ODE-solver and simulates until time t+T.
T : simulation time void step11::CUDADriver::run(double T) {
Start timer.
CUT_SAFE_CALL(cutStartTimer(timer));
Call to ODE solver.
ODESolve(t+T,new_val,new_val,solver);
Stop timer and print passed time.
CUT_SAFE_CALL(cutStopTimer(timer));
printf( "Processing time: %f (ms)\n", cutGetTimerValue(timer));
used_time=cutGetTimerValue(timer);
std::cout << new_val(hGetVecPos(1,2,N)) << std::endl; std::cout << new_val(hGetVecPos(2,1,N)) << std::endl;
}
This function transforms the FFTVector new_val into a vector of type std::vector<std::complex<double> >.
result : transformed vector void step11::CUDADriver::fetch(std::vector<std::complex<double> > &result) {
assert(aX.size()==new_val.size());
int k;
for (k=0; k<new_val.size(); k++){
result[k]=std::complex<double>(new_val(k).x,new_val(k).y);
}
}
This function performs a single explicit Euler-step at time t. Consider an ODE of the form
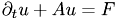 . Then an Euler step performs the following:
. Then an Euler step performs the following: 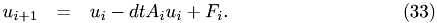
old_val : value calculated in previous step void step11::CUDADriver::EulerStep(MyVector &old_val) {
Calculates 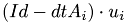 .
.
dCalcMatProd(tmp_val,old_val,dt,1.0,t);
Add right hand side (at time t).
RHside_tmp = RHside;
RHside_tmp*=(dt*dRHsideTime(t));
tmp_val+=RHside_tmp;
old_val=tmp_val;
}
This function performs a single implicit Euler step at time t. For the ODE
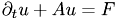 we have
we have 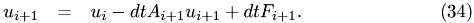
old_val : value calculated in previous step void step11::CUDADriver::ImplEulerStep(MyVector &old_val) {
RHside_tmp = RHside;
RHside_tmp*=(dt*dRHsideTime(t+dt));
RHside_tmp+=old_val;
dSolveGS(old_val,RHside_tmp,-dt,t+dt,3);
}
This function performs a single step via trapezoidal rule at time t. For the ODE
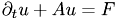 we have
we have 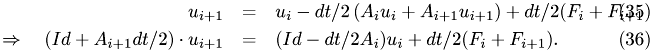
old_val : value calculated in previous step void step11::CUDADriver::TrapezoidalStep(MyVector &old_val) {
Calculate the right hand side of the linear system. First: Calculate 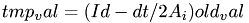 :
:
dCalcMatProd(tmp_val,old_val,dt/2.0, 1.0,t);
Second: tmp_val += dt/2*(RHside_{i+1} + RHside_i):
RHside_tmp = RHside;
RHside_tmp*= (dt/2.0*dRHsideTime(t));
tmp_val+=RHside_tmp;
RHside_tmp = RHside;
RHside_tmp*=(dt/2.0*dRHsideTime(t+dt));
tmp_val+=RHside_tmp;
Solve linear system using Gauss Seidel-iterations.
dSolveGS(old_val,tmp_val,-dt/2,t+dt, 3);
}
This function performs a single Runge-Kutta step at time t. For the ODE
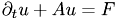 we have
we have 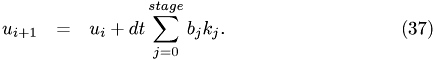
old_val : value calculated in previous step stage : stage of Runge-Kutta algorithm void step11::CUDADriver::RungeKuttaStep(MyVector &old_val, int stage) {
int i;
for (i=0; i<stage; i++) {
step_11_calcRKSumDummy(sum.array().val(),RK_k.array().val(),old_val.array().val(),dt,i,stage,N);
dCalcMatProd(tmp_val,sum,1.0,0.0,t+dt*getRK_c(i,stage),false);
RHside_tmp = RHside;
RHside_tmp*=dRHsideTime(t+dt*getRK_c(i,stage));
tmp_val+=RHside_tmp;
step_11_update_kDummy(tmp_val.array().val(),RK_k.array().val(),i,N);
}
step_11_update_valDummy(old_val.array().val(),RK_k.array().val(),dt,stage,N);
}
This is the ODE solver implemented on the GPU.
T : simulation time old_val : initial value new_val : result after time evolution T solver : choose ODE-solver void step11::CUDADriver::ODESolve(double T, MyVector &old_val, MyVector &new_val, int solver) {
std::cout << "GPU-ODE-Solver v. 0.5 (Codename Komsomol): dt=" << dt << ", T=" << T << std::endl;
new_val=old_val;
while (t<T) {
switch (solver) {
case ODE_EULER:
EulerStep(new_val);
break;
case ODE_TRAP:
TrapezoidalStep(new_val);
break;
case ODE_RK:
RungeKuttaStep(new_val, 4);
break;
case ODE_IMPL_EULER:
ImplEulerStep(new_val);
break;
}
t+=dt;
}
}
This function calculates the matrix vector product 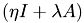 this. If nondiag is specified, the product lambda*(A-D)src is calculated, where A-D is A without its diagonal entries.
this. If nondiag is specified, the product lambda*(A-D)src is calculated, where A-D is A without its diagonal entries.
result : resulting vector lambda : 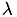
eta,: 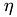
t,: time nondiag : if specified, use diagonal-free matrix void step11::CUDADriver::dCalcMatProd(MyVector &result, MyVector &rhs, double lambda, double eta, double t, bool nondiag) {
step_11_MatMultDummy(result.array().val(), aX.array().val(), aY.array().val(), rhs.array().val(), N, t, lambda, eta, nondiag);
}
This is an iterative solver for linear systems. This function implements the Gauss-Seidel algorithm. It assumes the linear system to be of the form
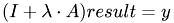 .
. 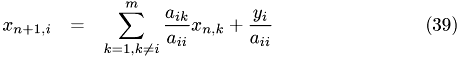
this : right hand side result : resulting vector (solution) lambda : 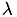
t : time iterations : number of iterations void step11::CUDADriver::dSolveGS(MyVector &result, MyVector &rhs, double lambda, double t, int iterations) {
unsigned int size=rhs.size();
assert((unsigned)rhs.size()==size);
assert(size==(unsigned int)(2*N+1)*(2*N+1));
FFTVector x_tmp((2*N+1)*(2*N+1));
result=rhs;
for (int k=0; k<iterations; k++) {
x_tmp=result;
step_11_GaussSeidelDummy(result.array().val(), aX.array().val(), aY.array().val(), x_tmp.array().val(), rhs.array().val(), N, t, lambda);
}
}
/ *void step11::CUDADriver::testFFT() {
int NX=16;
int NY=10;
int size=NX*sizeof(cuDoubleComplex);
cufftHandle plan;
cufftDoubleComplex *h_data1, *h_data2, *d_data1, *d_data2;
h_data1 = (cuDoubleComplex*)malloc(size);
h_data2 = (cuDoubleComplex*)malloc(size);
cudaMalloc( (void**)&d_data1, size );
cudaMalloc( (void**)&d_data2, size );
for(int i=0; i< NX; i++) {
h_data1[i].x = cos(2*M_PI*i/NX);
h_data1[i].y = 0.0;
}
cudaMemcpy(d_data1, h_data1, size, cudaMemcpyHostToDevice);
Create a 2D FFT plan
cufftPlan1d( &plan, NX, CUFFT_Z2Z, 1);
cufftExecZ2Z(plan, d_data1, d_data2, CUFFT_FORWARD );
cufftExecZ2Z(plan, d_data1, d_data2, CUFFT_INVERSE );
cudaMemcpy(h_data2, d_data2, size, cudaMemcpyDeviceToHost);
Destroy the CUFFT plan
cufftDestroy(plan);
cudaFree(d_data1);
cudaFree(d_data2);
for(int i = 0 ; i < NX ; i++){
printf("dataHost[%d] %f %f\n", i, h_data1[i].x, h_data1[i].y);
printf("data[%d] %f %f\n\n", i, h_data2[i].x, h_data2[i].y);
}
}* /
#endif // CUDA_DRIVER_STEP_11_HH
#ifndef CUDA_KERNEL_STEP_11_CU_H
#define CUDA_KERNEL_STEP_11_CU_H
void setParams(int __N, int __n, double __nu);
Declaration of Kernel Wrapper Functions
void step_11_MatMultDummy(cuDoubleComplex *result, cuDoubleComplex *aX, cuDoubleComplex *aY, cuDoubleComplex *input, int N, double t, double lambda, double eta, bool nondiag);
void step_11_GaussSeidelDummy(cuDoubleComplex *result, cuDoubleComplex *aX, cuDoubleComplex *aY, cuDoubleComplex *input, cuDoubleComplex *rhside, int N, double t, double lambda);
void step_11_calcRKSumDummy(cuDoubleComplex *partialSum, cuDoubleComplex *k, cuDoubleComplex *y, double dt, int m, int stage, int N);
void step_11_update_kDummy(cuDoubleComplex *partialSum, cuDoubleComplex *k, int m, int N);
void step_11_update_valDummy(cuDoubleComplex *result, cuDoubleComplex *k, double dt, int stage, int N);
#endif // CUDA_KERNEL_STEP_11_CU_H
Header-Datei der CUDA utility-Bibliothek.
#include <cutil_inline.h>
#include <cuda_kernel_wrapper_step-11.cu.h>
#include "cuda_driver_tools_step-11.h"
__constant__ double d_nu;
__constant__ int d_N;
__constant__ int d_n;
Host function to set the constant
void setParams(int __N, int __n, double __nu)
{
CUDA_SAFE_CALL(cudaMemcpyToSymbol("d_nu", (void**)&__nu, sizeof(__nu)));
CUDA_SAFE_CALL(cudaMemcpyToSymbol("d_N", (void**)&__N, sizeof(__N)));
CUDA_SAFE_CALL(cudaMemcpyToSymbol("d_n", (void**)&__n, sizeof(__n)));
}
These "Device Functions" are executable on the GPU only (and are automatically inline).
This function calculates the convolution of two vectors 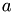 and src.
and src.
a,: first vector for convolution src,: second vector for convolution N : number of Fourier modes used for convolution t : time (a is dependent on time) __device__ ComplexNumber dCalcConv(ComplexNumber *aX, ComplexNumber *aY, ComplexNumber *src, int N, double t) {
int n1,n2,k1,k2;
int max_n1,min_n1,max_n2,min_n2;
ComplexNumber sum;
int pos1,pos2;
k1 = blockIdx.x*blockDim.x+threadIdx.x-N;
k2 = blockIdx.y*blockDim.y+threadIdx.y-N;
sum.x=0.0;
sum.y=0.0;
We have to make sure that no out-of-bounds accesses occur.
max_n1=dMin(k1+N,d_n);
min_n1=dMax(k1-N,-d_n);
max_n2=dMin(k2+N,d_n);
min_n2=dMax(k2-N,-d_n);
for (n1=min_n1; n1<=max_n1; n1++) {
Use helper variable to keep track of position in the array.
pos1=dGetVecPos(n1,min_n2,N);
pos2=dGetVecPos(k1-n1,k2-min_n2,N);
for (n2=min_n2; n2<=max_n2; n2++) {
sum-=((k1-n1)*aX[pos1]+(k2-n2)*aY[pos1])*src[pos2];
pos1++;
pos2--;
}
}
sum*=(ImUnit()*dATime(t));
return sum;
}
CUDA erweitert die Sprache C um sogenannte Kernel, deren parallele Ausfuehrung von den threads uebernommen wird. Um einen Kernel N-mal auszufuehren, muessen N threads gestartet werden. Wie das genau geht, wird spaeter an der entsprechenden Stelle erklaert.
Fuer die Parallelisierung reicht es vorerst zu wissen, dass in den Kernel-Funktionen das implementiert wird, was ein einzelner Rechenkern des Graphikchips machen soll. Allerdings sind dabei einige Feinheiten der Speicherarchitektur zu beachten, die sich auch in der Organisation der Gesamtheit aller threads niederschlaegt. Zwar kann jeder thread auf den gesamten Speicher der GPU zugreifen, allerdings dauert das einige Hundert Taktzyklen. Zur Abmilderung dieses Problems sind threads in Bloecken organisiert, innerhalb derer die threads ueber einen gemeinsamen schnellen Zwischenspeicher (shared memory) und Synchronisationspunkte kommunizieren koennen. Hingegen koennen threads aus verschiedenen Bloecken lediglich ueber den Hauptspeicher der GPU kommunizieren und besitzen keine Moeglichkeit der Synchronisation, laufen also voellig unabhaengig voneinander.
Die Besonderheit am shared memory ist, dass zwar die Zugriffszeiten vernachlaessigbar sind, dafuer aber immer 16 threads (ein sogenannter half-warp) gleichzeitig zugreifen, wodurch random access in der Regel enge Grenzen gesetzt sind.
This function calculates the matrix vector product 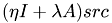 .
.
dest : resulting vector a : known vector field src : input vector t : time lambda : 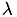
eta,: 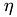
__global__ void __calcEntryThread(ComplexNumber *dest, ComplexNumber *aX, ComplexNumber *aY, ComplexNumber *src, double t, double lambda, double eta) {
ComplexNumber sum;
int k1 = blockIdx.x*blockDim.x+threadIdx.x-d_N;
int k2 = blockIdx.y*blockDim.y+threadIdx.y-d_N;
if ( (k1>d_N) || (k2>d_N) )
return;
sum = dCalcConv(aX, aY, src, d_N, t);
sum-=d_nu*((double)(k1*k1+k2*k2))*src[dGetVecPos(k1,k2,d_N)];
Insert result into the forumla 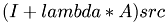 .
.
dest[dGetVecPos(k1,k2,d_N)] = eta*src[dGetVecPos(k1,k2,d_N)]+lambda*sum;
}
Kernel: calcEntryThreadNonDiag
This function calculates the matrix vector product 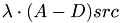 is calculated, where
is calculated, where 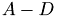 is
is 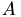 without its diagonal entries.
without its diagonal entries.
dest : resulting vector a : known vector field src : input vector t : time lambda : 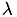
__global__ void __calcEntryThreadNonDiag(ComplexNumber *dest, ComplexNumber *aX, ComplexNumber *aY, ComplexNumber *src, double t, double lambda) {
ComplexNumber sum;
int k1 = blockIdx.x*blockDim.x+threadIdx.x-d_N;
int k2 = blockIdx.y*blockDim.y+threadIdx.y-d_N;
if ( (k1>d_N) || (k2>d_N) ){
return;
}
sum = dCalcConv(aX, aY, src, d_N, t);
For GaussSeidel do NOT add the diagonal entry (i.e. n1=0, n2=0) to sum (so do reverse operation).
sum+=((double) k1*aX[dGetVecPos(0,0,d_N)]+(double) k2*aY[dGetVecPos(0,0,d_N)]) * ImUnit() * src[dGetVecPos(k1,k2,d_N)] * dATime(t);
I is diagonal, so ignore Identity matrix in this case.
dest[dGetVecPos(k1,k2,d_N)] = lambda*sum;
}
This is used in the Gauss-Seidel iterative solver for linear systems. It assumes the linear system to be of the form 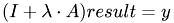 .
.
dest : resulting vector (solution) a : known vector field src : input vector, used for calculation of the matrix 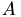
rhside : right hand side 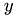
t : time lambda : 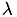
__global__ void __calcGaussSeidelThread(ComplexNumber *dest, ComplexNumber *aX, ComplexNumber *aY, ComplexNumber *src, ComplexNumber *rhside, double t, double lambda) {
int k1,k2;
ComplexNumber tmp;
ComplexNumber sum;
k1 = blockIdx.x*blockDim.x+threadIdx.x-d_N;
k2 = blockIdx.y*blockDim.y+threadIdx.y-d_N;
if ( (k1>d_N) || (k2>d_N) ){
return;
}
sum = dCalcConv(aX, aY, src, d_N, t);
For GaussSeidel do NOT add the diagonal entry (i.e. n1=0, n2=0) to sum (so do reverse operation).
sum+=((double) k1*aX[dGetVecPos(0,0,d_N)]+(double) k2*aY[dGetVecPos(0,0,d_N)]) * ImUnit() * src[dGetVecPos(k1,k2,d_N)]*dATime(t);
I is diagonal, so ignore Identity matrix in this case.
sum = lambda*sum;
sum = rhside[dGetVecPos(k1,k2,d_N)] - sum;
tmp=d_nu*(k1*k1+k2*k2) + ( ((double) k1*aX[dGetVecPos(0,0,d_N)]+(double) k2*aY[dGetVecPos(0,0,d_N)])*ImUnit()*dATime(t));
dest[dGetVecPos(k1,k2,d_N)] = sum/( 1.0+ ((-1.0)*lambda*tmp) );
}
__global__ void __calcRKSum(ComplexNumber *partialSum, ComplexNumber *k, ComplexNumber *y, double dt, int m, int stage) {
int k1,k2,i;
k1 = blockIdx.x*blockDim.x+threadIdx.x-d_N;
k2 = blockIdx.y*blockDim.y+threadIdx.y-d_N;
if ( (k1>d_N) || (k2>d_N) ){
return;
}
int size=(2*d_N+1)*(2*d_N+1);
ComplexNumber sum;
sum.x=0.0;
sum.y=0.0;
ComplexNumber tmp;
for (i=0; i<m; i++) {
tmp = dGetRK_A(m,i,stage)*k[i*size+dGetVecPos(k1,k2,d_N)];
sum += tmp;
}
sum=dt*sum;
sum+=y[dGetVecPos(k1,k2,d_N)];
partialSum[dGetVecPos(k1,k2,d_N)] = sum;
printf("%d, %f\n",m,sum.x);
}
__global__ void __update_k(ComplexNumber *partialSum, ComplexNumber *k, int m) {
int k1,k2;
k1 = blockIdx.x*blockDim.x+threadIdx.x-d_N;
k2 = blockIdx.y*blockDim.y+threadIdx.y-d_N;
if ( (k1>d_N) || (k2>d_N) ){
return;
}
int size=(2*d_N+1)*(2*d_N+1);
k[m*size+dGetVecPos(k1,k2,d_N)] = partialSum[dGetVecPos(k1,k2,d_N)];
}
__global__ void __update_val(ComplexNumber *result, ComplexNumber *k, double dt, int stage) {
int k1,k2,i;
k1 = blockIdx.x*blockDim.x+threadIdx.x-d_N;
k2 = blockIdx.y*blockDim.y+threadIdx.y-d_N;
if ( (k1>d_N) || (k2>d_N) ){
return;
}
int size=(2*d_N+1)*(2*d_N+1);
ComplexNumber sum;
sum.x=0.0;
sum.y=0.0;
for (i=0; i<stage; i++) {
sum=sum+dGetRK_b(i,stage)*k[i*size+dGetVecPos(k1,k2,d_N)];
}
result[dGetVecPos(k1,k2,d_N)] += dt*sum;
}
There is a wrapper function for each kernel which organizes the partition of the threads and starts them.
Function: step_11_MatMultDummy
This function starts the kernels for calculation of the matrix vector product.
result : resulting vector a=(aX,aY) : known velocity field input,: input vector N : number of Fourier modes t,: time lambda : 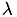
eta,: 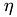
nondiag : if specified, use diagonal-free matrix void step_11_MatMultDummy(ComplexNumber *result, ComplexNumber *aX, ComplexNumber *aY, ComplexNumber *input, int N, double t, double lambda, double eta, bool nondiag)
{
dim3 grid;
dim3 blocks;
calcCudaParams(grid,blocks,N);
if (nondiag)
__calcEntryThreadNonDiag<<<grid, blocks>>>(result, aX, aY, input, t, lambda);
else
__calcEntryThread<<<grid, blocks>>>(result, aX, aY, input, t, lambda, eta);
cudaThreadSynchronize();
}
Function: step_11_GaussSeidelDummy
This function organizes Gauss Seidel solver.
result : resulting vector a : known velocity field input,: input vector (used to calculate the matrix) rhside,: right hand side of the linear system N : number of Fourier modes t,: time lambda : 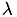
void step_11_GaussSeidelDummy(ComplexNumber *result, ComplexNumber *aX, ComplexNumber *aY, ComplexNumber *input, ComplexNumber *rhside, int N, double t, double lambda)
{
dim3 grid;
dim3 blocks;
calcCudaParams(grid,blocks,N);
__calcGaussSeidelThread<<<grid, blocks>>>(result, aX, aY, input, rhside, t, lambda);
cudaThreadSynchronize();
}
Function: step_11_calcRKSumDummy
void step_11_calcRKSumDummy(ComplexNumber *partialSum, ComplexNumber *k, ComplexNumber *y, double dt, int m, int stage, int N) {
dim3 grid;
dim3 blocks;
calcCudaParams(grid,blocks,N);
__calcRKSum<<<grid, blocks>>>(partialSum, k, y, dt, m, stage);
cudaThreadSynchronize();
}
Function: step_11_update_kDummy
void step_11_update_kDummy(ComplexNumber *partialSum, ComplexNumber *k, int m, int N) {
dim3 grid;
dim3 blocks;
calcCudaParams(grid,blocks,N);
__update_k<<<grid, blocks>>>(partialSum, k, m);
cudaThreadSynchronize();
}
Function: step_11_update_valDummy
void step_11_update_valDummy(ComplexNumber *result, ComplexNumber *k, double dt, int stage, int N) {
dim3 grid;
dim3 blocks;
calcCudaParams(grid,blocks,N);
__update_val<<<grid, blocks>>>(result, k, dt, stage);
cudaThreadSynchronize();
}
STL header
#include <iostream>
#include <vector>
#include <math.h>
Treiber fuer den GPU-Teil
#include "cuda_driver_step-11.h"
Treiber fuer den CPU-Teil
#include "cpu_driver_step-11.h"
deal.II-Komponenten
#include <lac/vector.h>
#include <lac/blas++.h>
cublas-Wrapper-Klassen. Binden alle sonstigen benoetigten header-Dateien ein.
#include "cuda_driver_step-11.hh"
#include "cpu_driver_step-11.hh"
#include "cuda_driver_tools_step-11.h"
#include "fancy_vector.h"
#include "fancy_vector.hh"
#define USE_DEAL_II
#undef USE_DEAL_II
using namespace step11;
namespace step11 {
This class regulates the simulation and the use of CPU or GPU version.
class MyFancySimulation {
public:
MyFancySimulation();
void run();
private:
void save(double t, std::string name);
void getRHSorA(std::vector<std::complex<double> > &_RHside, double(step11::MyFancySimulation::*f)(double,double));
inline double originalRHS(double x, double y);
inline double originalAX(double x, double y);
inline double originalAY(double x, double y);
void dFFT(int NX, int NY, cufftDoubleComplex *h_dataIn, cufftDoubleComplex *h_dataOut, bool inverse=false);
void sortVecFFT(cufftDoubleComplex *h_dataIn, int size);
int hSelftest();
double calcError(std::vector<std::complex<double> > &result, double T);
CUDADriver cudaDriver;
CPUDriver cpuDriver;
std::vector<std::complex<double> > result;
int N,n;
double nu;
int solver;
double T;
double dt;
};
}
Konstruktor: MyFancySimulation
step11::MyFancySimulation::MyFancySimulation()
{
}
Determination of Right Hand Side (space dimensions) of the PDE
inline double step11::MyFancySimulation::originalRHS(double x, double y) {
return cos(x+y);
}
Determination of aX (space dimensions)
inline double step11::MyFancySimulation::originalAX(double x, double y) {
return 1.0;
}
Determination of aY (space dimensions)
inline double step11::MyFancySimulation::originalAY(double x, double y) {
return 1.0;
}
Calculation of the FFT of RHS/a
void step11::MyFancySimulation::getRHSorA(std::vector<std::complex<double> > &_RHside, double(step11::MyFancySimulation::*f)(double,double)) {
assert(_RHside.size()==(unsigned int)(2*N+1)*(2*N+1));
int size=(2*N+1)*(2*N+1)*sizeof(ComplexNumber);
int i, j;
Insert sampling points 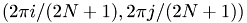 in order to obtain a discrete vector.
in order to obtain a discrete vector.
for (j=0; j< (2*N+1); j++) {
for (i=0; i< (2*N+1); i++) {
_RHside[j*(2*N+1)+i]= originalRHS(2.0*M_PI*i/(2*N+1), 2.0*M_PI*j/(2*N+1));
_RHside[j*(2*N+1)+i]= (*this.*f)(2.0*M_PI*i/(2*N+1), 2.0*M_PI*j/(2*N+1));
}
}
FFT of the vector _RHside. FFT is done on GPU, so we have to create an associate vector FFT_RHside on GPU.
cufftDoubleComplex *FFT_RHside;
FFT_RHside = (cuDoubleComplex*)malloc(size);
for (i=0; i<(2*N+1)*(2*N+1); i++) {
FFT_RHside[i].x = std::real(_RHside[i]);
FFT_RHside[i].y = std::imag(_RHside[i]);
}
dFFT(2*N+1, 2*N+1, FFT_RHside, FFT_RHside, false);
for (i=0; i<(2*N+1)*(2*N+1); i++) {
_RHside[i] = std::complex<double>(FFT_RHside[i].x,FFT_RHside[i].y);
}
free(FFT_RHside);
}
void step11::MyFancySimulation::run() {
hSelftest();
return;
Initialize parameters used in simulation.
N : number of Fourier modes (we use 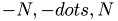 )
) n : number of modes used in convolution dt : time step T : simulation time solver,: choose the solver used (explicit Euler, trapezoidal, Runge-Kutta4) int k1,k2;
N=5;
n=5;
nu=0.1;
T=0.01;
dt=1e-4;
solver=ODE_TRAP;
double t=0.0;
double delta_t=0.1;
a : a=(aX,aY) is a known velocity field (see Oseen-problem) in momentum space RHside : right hand side of PDE in momentum space initVal : initial values std::vector<std::complex<double> > aX((2*N+1)*(2*N+1));
std::vector<std::complex<double> > aY((2*N+1)*(2*N+1));
std::vector<std::complex<double> > RHside((2*N+1)*(2*N+1));
std::vector<std::complex<double> > initVal((2*N+1)*(2*N+1));
result.resize((2*N+1)*(2*N+1));
for (k1=-N; k1<=N; k1++) {
for (k2=-N; k2<=N; k2++) {
initialise known field a. Use decaying Fourier coefficients to minimize truncation errors
aX[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
aY[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
initialise right hand side
RHside[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
set initial values
initVal[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
}
}
compute right hand side in momentum space getRHSorA(RHside, &step11::MyFancySimulation::originalRHS); compute known field a in momentum space getRHSorA(aX, &step11::MyFancySimulation::originalAX); getRHSorA(aY, &step11::MyFancySimulation::originalAY);
set initial conditions initVal[hGetVecPos(1,2,N)]=1.0; initVal[hGetVecPos(2,1,N)]=1.0;
write data to file (GPU-version)
/ * cudaDriver.init(N, n, nu, solver, dt, initVal, a, RHside);
cudaDriver.fetch(result);
save(t, "data/test");
while (t<T) {
cudaDriver.run(delta_t);
cudaDriver.fetch(result);
save(t, "data/test");
std::cout << result[hGetVecPos(1,2,N)] << std::endl;
t+=delta_t;
}
* /
std::cout << "init GPU..." << std::endl;
run simulation on GPU
cudaDriver.init(N, n, nu, solver, dt, initVal, aX, aY, RHside);
cudaDriver.run(T,solver);
cudaDriver.fetch(result);
std::cout << result[hGetVecPos(1,2,N)] << std::endl;
run simulation on CPU
/ *cpuDriver.init(N, n, nu, solver, dt, initVal, aX, aY, RHside);
cpuDriver.run(T);
cpuDriver.fetch(result);
std::cout << result[hGetVecPos(1,2,N)] << std::endl;* /
return;
}
This function calculates the velocity field 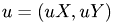 by inverse FFT and organizes the storage of data at time t.
by inverse FFT and organizes the storage of data at time t.
t : time string name : filename void step11::MyFancySimulation::save(double t, std::string name) {
int size=(2*N+1)*(2*N+1)*sizeof(ComplexNumber);
int i,k,k1,k2;
double x, y, u_norm;
Calculate fourier coeffs of velocity field (uX,uY) knowing
 , where
, where 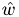 is stored in result:
is stored in result: 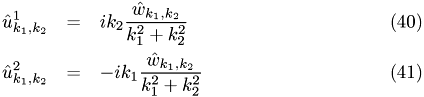
cufftDoubleComplex *uX, *uY;
uX = (cuDoubleComplex*)malloc(size);
uY = (cuDoubleComplex*)malloc(size);
for (k1=-N; k1<=N; k1++) {
for (k2=-N; k2<=N; k2++) {
uX[hGetVecPos(k1,k2,N)].x = std::real(result[hGetVecPos(k1,k2,N)]);
uX[hGetVecPos(k1,k2,N)].y = std::imag(result[hGetVecPos(k1,k2,N)]);
uY[hGetVecPos(k1,k2,N)] = uX[hGetVecPos(k1,k2,N)];
uX[hGetVecPos(k1,k2,N)]*= ((double)k2)/(k1*k1+k2*k2)*ImUnit();
uY[hGetVecPos(k1,k2,N)]*= -((double)k1)/(k1*k1+k2*k2)*ImUnit();
}
}
uX[hGetVecPos(0,0,N)]=0.0*ImUnit();
uY[hGetVecPos(0,0,N)]=0.0*ImUnit();
sort entries of uX and uY to ensure right order of wave numbers
sortVecFFT(uX, size);
sortVecFFT(uY, size);
obtain velocity field in position-space by applying inverse FFT
dFFT(2*N+1, 2*N+1, uX, uX, true);
dFFT(2*N+1, 2*N+1, uY, uY, true);
save data in file
std::ostringstream filename;
filename << name << t << ".dat";
std::ofstream f;
f.open(filename.str().c_str(), std::ios::out);
save x-coordinate, y-coordinate and norm of velocity field
for (i=0; i<2*N+1; i++) {
for (k=0; k<2*N+1; k++) {
x = 2.0*M_PI*i/(2*N+1);
y = 2.0*M_PI*k/(2*N+1);
u_norm = sqrt( uX[k*(2*N+1)+i].x* uX[k*(2*N+1)+i].x + uY[k*(2*N+1)+i].x* uY[k*(2*N+1)+i].x);
f << x << "\t" << y << "\t" << u_norm << std::endl;
}
f << std::endl;
}
f << std::endl;
f.close();
free(uX);
free(uY);
}
This function sorts the entries of input vector (before FFT) to ensure right order of wave numbers.
h_dataIn : input data size : size of input data void step11::MyFancySimulation::sortVecFFT(cufftDoubleComplex *h_dataIn, int size){
ComplexNumber *tmp;
tmp = (ComplexNumber*)malloc(size);
Sort entries of h_dataIn in order to get right order of fourier modes.
cufftDoubleComplex *ordered;
ordered = (cuDoubleComplex*)malloc(size);
Sort columns of the vector as follows: For one row: the 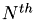 -
-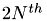 entries have to be first, entries 0 till
entries have to be first, entries 0 till 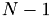 have to be at the end.
have to be at the end.
for(int i = 0 ; i < 2*N+1 ; i++){
for(int k=0; k<N; k++){
ordered[k+i*(2*N+1)+N+1] = h_dataIn[k+i*(2*N+1)];
ordered[k+i*(2*N+1)] = h_dataIn[k+i*(2*N+1)+N];
}
ordered[N+i*(2*N+1)] = h_dataIn[N+i*(2*N+1)+N];
}
memcpy(tmp,ordered,size);
Sort rows: same as for columns.
for(int k = 0 ; k < 2*N+1 ; k++){
for(int i=0; i<N; i++){
ordered[k+(i+1)*(2*N+1)+N*(2*N+1)] = tmp[k+i*(2*N+1)];
ordered[k+i*(2*N+1)] = tmp[k+i*(2*N+1)+N*(2*N+1)];
}
ordered[k+N*(2*N+1)] = tmp[k+N*(2*N+1)+N*(2*N+1)];
}
memcpy(h_dataIn,ordered,size);
}
This function does 2-dimensional FFT or inverse FFT (on GPU).
NX : size in x-direction NY : size in y-direction h_dataIn : input data h_dataOut : output data, i.e. the transformed vector invese : determines if forward or inverse FFT is needed void step11::MyFancySimulation::dFFT(int NX, int NY, cufftDoubleComplex *h_dataIn, cufftDoubleComplex *h_dataOut, bool inverse) {
int size=NX*NY*sizeof(cuDoubleComplex);
cufftHandle plan;
cufftDoubleComplex *d_dataIn, *d_dataOut;
cudaMalloc( (void**)&d_dataIn, size );
cudaMalloc( (void**)&d_dataOut, size );
cudaMemcpy(d_dataIn, h_dataIn, size, cudaMemcpyHostToDevice);
Create a 2D FFT plan.
cufftPlan2d( &plan, NX, NY, CUFFT_Z2Z);
Forward FFT:
if(!inverse) {
cufftExecZ2Z(plan, d_dataIn, d_dataOut, CUFFT_FORWARD );
}
Inverse FFT:
else {
cufftExecZ2Z(plan, d_dataIn, d_dataOut, CUFFT_INVERSE );
}
cudaThreadSynchronize();
cudaMemcpy(h_dataOut, d_dataOut, size, cudaMemcpyDeviceToHost);
Destroy the CUFFT plan.
cufftDestroy(plan);
cudaFree(d_dataIn);
cudaFree(d_dataOut);
Normalize the resulting vector in case of inverse FFT.
if(inverse) {
for(int i = 0 ; i < NX*NY ; i++){
h_dataOut[i] = 1.0/(NX*NY) *h_dataOut[i];
}
}
}
This function tests the simulation.
int MyFancySimulation::hSelftest() {
int k1,k2,i,j,k,num_iter;
N=20;
n=20;
nu=0.1;
T=0.1;
dt=1e-3;
solver=ODE_RK;
std::vector<std::complex<double> > aX((2*N+1)*(2*N+1));
std::vector<std::complex<double> > aY((2*N+1)*(2*N+1));
std::vector<std::complex<double> > RHside((2*N+1)*(2*N+1));
std::vector<std::complex<double> > initVal((2*N+1)*(2*N+1));
result.resize((2*N+1)*(2*N+1));
/ * for (k1=-N; k1<=N; k1++) {
for (k2=-N; k2<=N; k2++) {
Initialise known field a. Use decaying Fourier coefficients to minimize truncation errors.
aX[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
aY[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
Initialise right hand side.
RHside[hGetVecPos(k1,k2,N)]=0.0;
int max_n1,min_n1,max_n2,min_n2;
max_n1=std::min(k1+N,n);
min_n1=std::max(k1-N,-n);
max_n2=std::min(k2+N,n);
min_n2=std::max(k2-N,-n);
for (int n1=min_n1; n1<=max_n1; n1++) {
for (int n2=min_n2; n2<=max_n2; n2++) {
RHside[hGetVecPos(k1,k2,N)]+=((double)(k1-n1+k2-n2)/( (((k1-n1)*(k1-n1))+1)*((k2-n2)*(k2-n2)+1)*(n1*n1+1)*(n2*n2+1)) );
}
}
RHside[hGetVecPos(k1,k2,N)]*=std::complex<double>(0.0,1.0);
RHside[hGetVecPos(k1,k2,N)]+=nu*(k1*k1+k2*k2-1)/((k1*k1+1)*(k2*k2+1));
Set initial values.
initVal[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
}
}
double errorL2[4]={0.0,0.0,0.0,0.0};
std::ofstream f;
f.open("data/errors.dat", std::ios::out);
dt=1.0;
for (i=1; i<30; i++) {
dt=dt/2.0;
for (j=1; j<5; j++) {
solver=j;
cudaDriver.init(N, n, nu, solver, dt, initVal, aX, aY, RHside);
cudaDriver.run(T);
cudaDriver.fetch(result);
errorL2[j-1] = calcError(result,T);
}
f << dt << "\t" << errorL2[0] << "\t" << errorL2[1] << "\t" << errorL2[2] << "\t" << errorL2[3] << std::endl;
}
f.close();
* /
double times[8]={0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0};
double sigmas[8]={0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0};
double times_tmp[10];
std::ofstream f;
f.open("data/times.dat", std::ios::out | std::ios::app);
dt=1e-4;
T=0.01;
N=34;
num_iter=10;
CUDADriver *cudaDriver_tmp;
for (i=1; i<30; i++) {
N+=2;
n=N;
std::cout << std::endl << "N=" << N << std::endl;
aX.resize((2*N+1)*(2*N+1));
aY.resize((2*N+1)*(2*N+1));
RHside.resize((2*N+1)*(2*N+1));
initVal.resize((2*N+1)*(2*N+1));
result.resize((2*N+1)*(2*N+1));
for (k1=-N; k1<=N; k1++) {
for (k2=-N; k2<=N; k2++) {
initialise known field a. Use decaying Fourier coefficients to minimize truncation errors
aX[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
aY[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
initialise right hand side
RHside[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
set initial values
initVal[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
}
}
cudaDriver.init(N, n, nu, solver, dt, initVal, aX, aY, RHside);
for (j=1; j<5; j++) {
solver=j;
std::cout << "GPU, solver=" << j << std::endl;
for (k=0; k<num_iter; k++) {
cudaDriver_tmp = new CUDADriver; cudaDriver_tmp->init(N, n, nu, solver, dt, initVal, aX, aY, RHside);
cudaDriver.reset(initVal);
cudaDriver.run(T,solver);
cudaDriver.fetch(result);
times[j-1] += cudaDriver.used_time;
times[k] = cudaDriver.used_time;
delete cudaDriver_tmp;
}
times[j-1]/=num_iter;
for (k=0; k<num_iter; k++) {
sigmas[j-1]+=((times_tmp[k]-times[j-1])*(times_tmp[k]-times[j-1]));
sigmas[j-1]=sqrt(sigmas[j-1]/(num_iter-1));
}
}
for (j=1; j<5; j++) {
solver=j;
std::cout << "CPU, solver=" << j << std::endl;
for (k=0; k<num_iter; k++) {
cpuDriver.init(N, n, nu, solver, dt, initVal, aX, aY, RHside);
cpuDriver.run(T);
cpuDriver.fetch(result);
times[4+j-1] += cpuDriver.used_time;
times_tmp[k] = cpuDriver.used_time;
}
times[4+j-1]/=num_iter;
for (k=0; k<num_iter; k++) {
sigmas[4+j-1]+=((times_tmp[k]-times[4+j-1])*(times_tmp[k]-times[4+j-1]));
sigmas[4+j-1]=sqrt(sigmas[4+j-1]/(num_iter-1));
}
}
f << N << "\t" << times[0] << "\t" << times[1] << "\t" << times[2] << "\t" << times[3] << "\t" << times[4] << "\t" << times[5] << "\t" << times[6] << "\t" << times[7] << "\t" << sigmas[0] << "\t" << sigmas[1] << "\t" << sigmas[2] << "\t" << sigmas[3] << "\t" << sigmas[4] << "\t" << sigmas[5] << "\t" << sigmas[6] << "\t" << sigmas[7] << std::endl;
}
f.close();
return true;
}
double MyFancySimulation::calcError(std::vector<std::complex<double> > &result, double T) {
double errorL2=0.0;
std::complex<double> error_tmp;
int k1,k2;
for (k1=-N; k1<=N; k1++) {
for (k2=-N; k2<=N; k2++) {
error_tmp = result[hGetVecPos(k1,k2,N)]-std::complex<double>(exp(-nu*T)*1.0/((k1*k1+1.0)*(k2*k2+1.0)), 0.0);
errorL2 += std::abs(error_tmp)*std::abs(error_tmp);
}
}
return(sqrt(errorL2));
}
int main(int / *argc* /, char * / *argv* /[])
{
using namespace step11;
MyFancySimulation machma;
machma.run();
}
Results
We first show two generic simulations.
The first simulation shows the homogeneous problem. We have
with
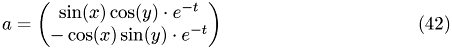
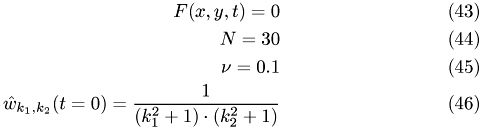
Norm of velocity u at t=0 Norm of velocity u at t=1.2 Norm of velocity u at t=3.4 Norm of velocity u at t=6.9 Norm of velocity u at t=10.4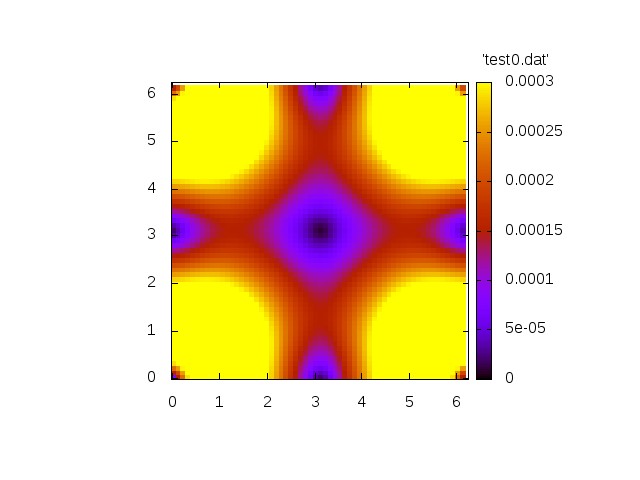
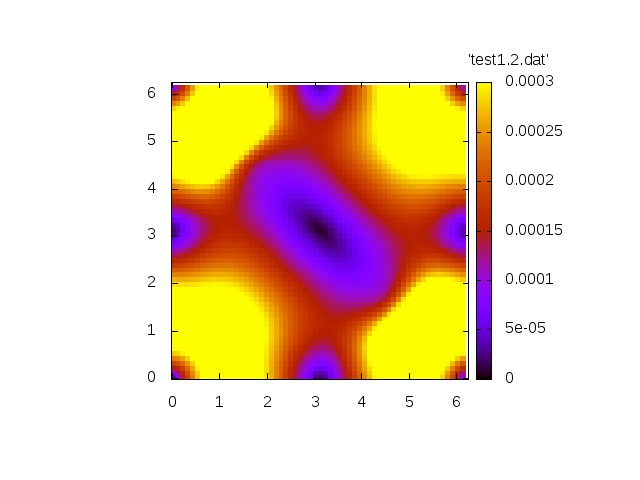
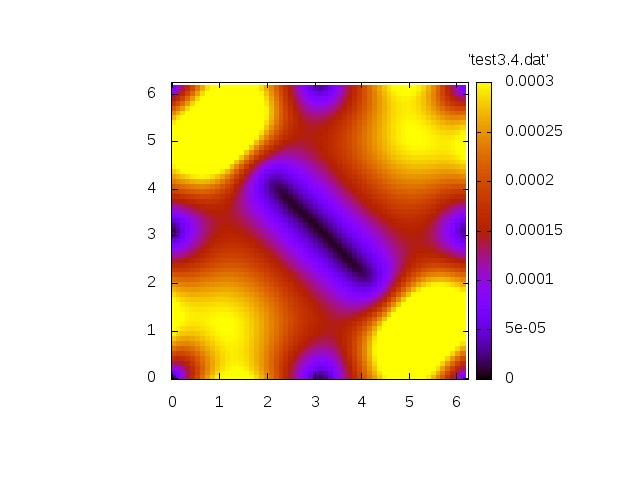
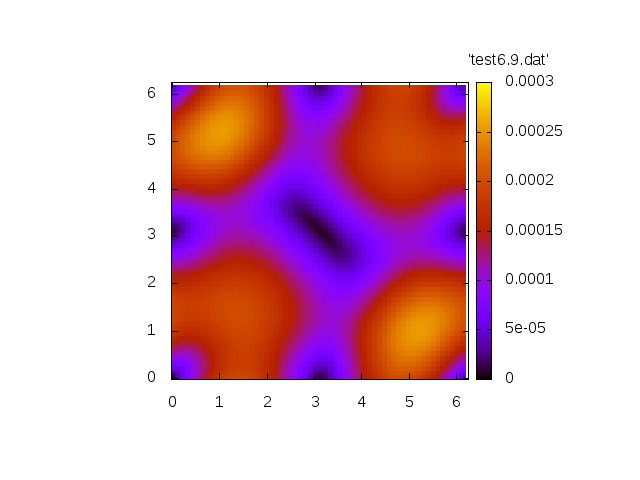
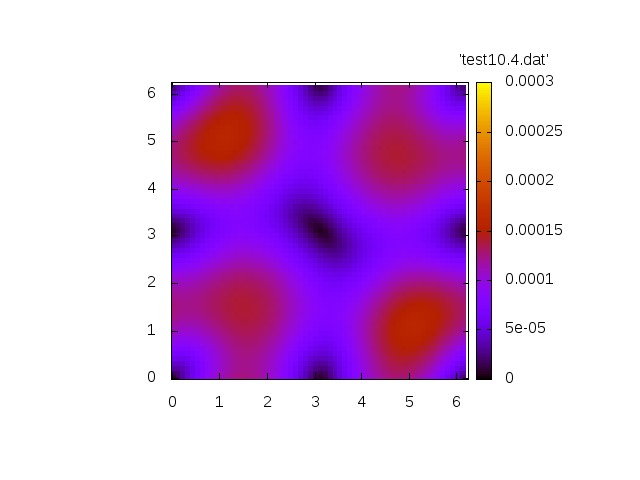
Now we show a simulation with a non.vanishing right-hand side.
with
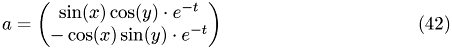
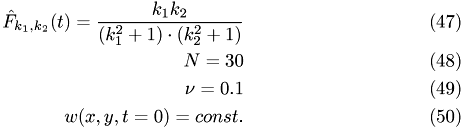
Norm of velocity u at t=0 Norm of velocity u at t=1.6 Norm of velocity u at t=2.5 Norm of velocity u at t=4.4 Norm of velocity u at t=8.6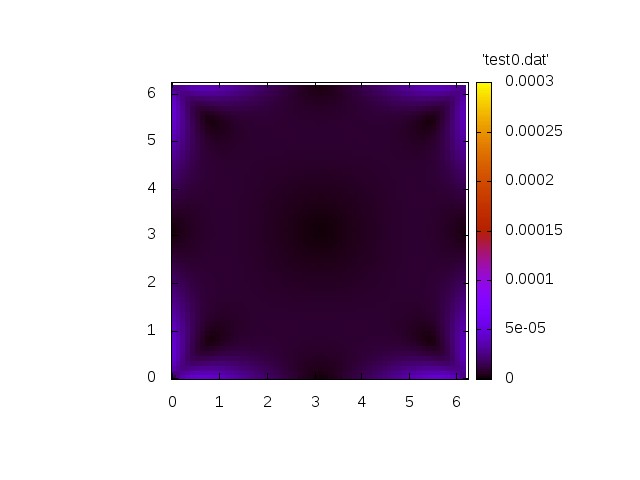
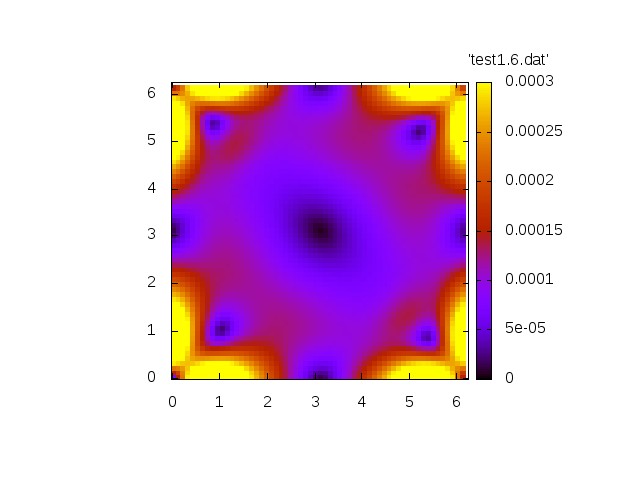
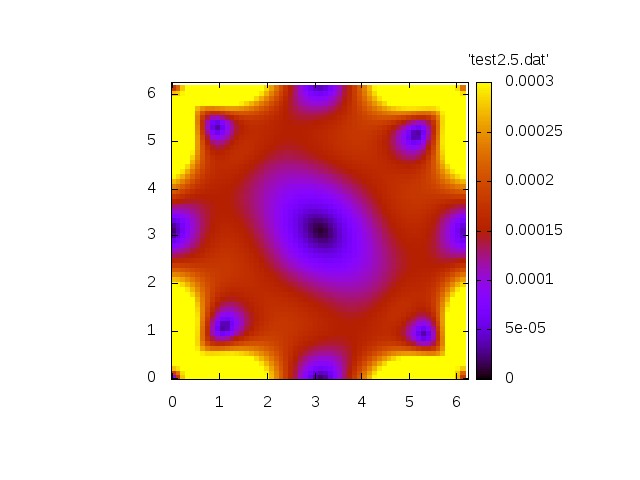

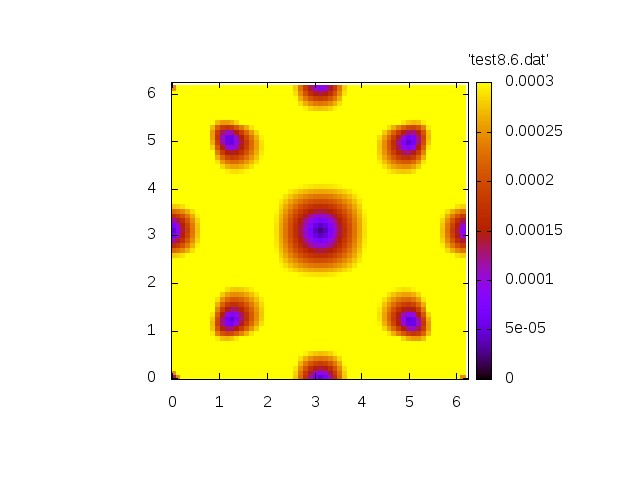
Both simulations show qualitatively correct behaviour. The source-free case shows a decay whereas the inhomogeneous case exhibit a grow in amplitude.
Comparison of the used ODE-solvers
We choosed coefficient functions and a right-hand side in such a way that we can solve the ODE system analytically. We then compare the numerical solution with the analytical one.
The used setting is:
with
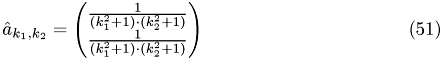
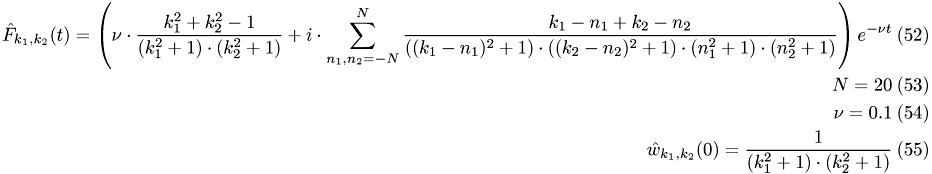
Error for $ w$ of ODE-solvers compared to analytical solution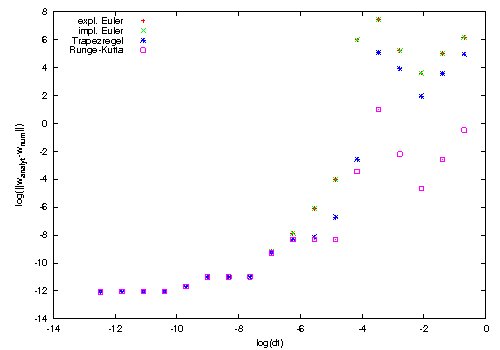
Runge-Kutta is the only algorithm which stays stable even for large step sizes. Overall, we encounter no severe stability problems with any of the implemented solvers.
We measured the runtime improvement of the CUDA implementation with respect to a CPU implementation. We spend ca. three days optimizing the CPU version so this is not an unfair comparison. The x-axis shows the number of oscillators N used in the simulation. At each N we performed 10 iterations for each of the four solvers on the CPU and then the same on the GPU.
Overall, we see a very nice speedup of roughly a factor of 17. The large fluctuations on the right hand side of the plot are due to interference effects with our groups using the GPU at the same time.
The used setting is:
with
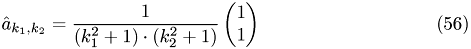
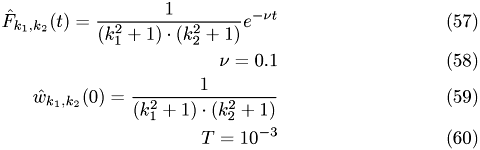
Runtime CPU/runtime GPU (10 iterations)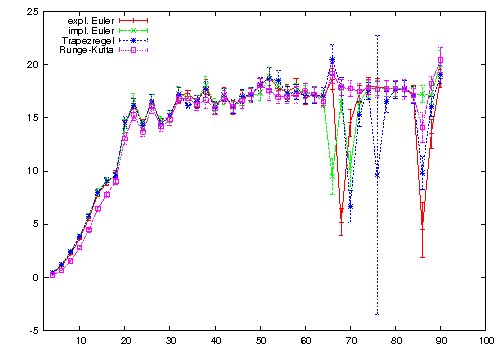
(If you are looking at a locally installed CUDA HPC Praktikum version, then the program can be found at .. /.. /testsite / /step-11 /step-cu.cc . Otherwise, this is only the path on some remote server.) #ifndef CPU_DRIVER_STEP11_H
#define CPU_DRIVER_STEP11_H
namespace step11 {
#include "cuda_driver_tools_step-11.h"
class CPUDriver {
public:
typedef ::Vector<std::complex<double> > MyVector;
typedef ::FullMatrix<std::complex<double> > MyMatrix;
typedef ::Vector<double> RKVector;
CPUDriver() {
timer=0;
}
~CPUDriver ();
void init(int _N, int _n, double _nu, int _solver, double _dt, std::vector<std::complex<double> > &__init_val, std::vector<std::complex<double> > &_aX, std::vector<std::complex<double> > &_aY, std::vector<std::complex<double> > &_RHside);
void run(double T);
void fetch(std::vector<std::complex<double> > &result);
void EulerStep(MyVector &old_val);
void ImplEulerStep(MyVector &old_val);
void TrapezoidalStep(MyVector &old_val);
void RungeKuttaStep(MyVector &old_val, int stage);
void ODESolve(double T, MyVector &old_val, MyVector &new_val, int solver);
void CalcEntry(double _t, double eta, double lambda, MyVector &dest, MyVector &src, bool nondiag);
void GaussSeidel(double _t, double lambda, MyVector &result, MyVector &y, int iterations);
double used_time;
private:
MyVector tmp_val;
MyVector init_val;
MyVector new_val;
MyVector aX;
MyVector aY;
MyVector RHside;
MyVector RHside_tmp;
int N;
int n;
double nu;
int solver;
unsigned int timer;
double dt;
double t;
};
}//end of namespace
#endif // CPU_DRIVER_STEP11_H
#ifndef CPU_DRIVER_STEP_11_HH
#define CPU_DRIVER_STEP_11_HH
#include "cpu_driver_step-11.h"
#include "tools_step-11.h"
step11::CPUDriver::~CPUDriver()
{
if (timer) {
CUT_SAFE_CALL(cutDeleteTimer(timer));
}
}
void step11::CPUDriver::init(int _N, int _n, double _nu, int _solver, double _dt, std::vector<std::complex<double> > &_init_val, std::vector<std::complex<double> > &_aX, std::vector<std::complex<double> > &_aY, std::vector<std::complex<double> > &_RHside) {
unsigned int k;
N=_N;
n=_n;
nu=_nu;
dt=_dt;
solver=_solver;
t=0.0;
used_time=0.0;
init_val.reinit((2*N+1)*(2*N+1));
new_val.reinit((2*N+1)*(2*N+1));
tmp_val.reinit((2*N+1)*(2*N+1));
aX.reinit((2*N+1)*(2*N+1),false);
aY.reinit((2*N+1)*(2*N+1),false);
RHside.reinit((2*N+1)*(2*N+1),false);
RHside_tmp.reinit((2*N+1)*(2*N+1),false);
for (k=0; k<init_val.size(); k++) {
init_val(k)=_init_val[k];
}
for (k=0; k<aX.size(); k++) {
aX(k)=_aX[k];
aY(k)=_aY[k];
}
for (k=0; k<RHside.size(); k++) {
RHside(k)=_RHside[k];
}
new_val=init_val;
if (timer) {
CUT_SAFE_CALL(cutDeleteTimer(timer));
}
CUT_SAFE_CALL(cutCreateTimer(&timer));
}
void step11::CPUDriver::run(double T) {
CUT_SAFE_CALL(cutStartTimer(timer));
ODESolve(t+T,new_val,new_val,solver);
CUT_SAFE_CALL(cutStopTimer(timer));
printf( "Processing time: %f (ms)\n", cutGetTimerValue(timer));
used_time=cutGetTimerValue(timer);
}
void step11::CPUDriver::fetch(std::vector<std::complex<double> > &result) {
assert(aX.size()==new_val.size());
unsigned int k;
for (k=0; k<new_val.size(); k++){
result[k]=new_val(k);
}
}
void step11::CPUDriver::EulerStep(MyVector &old_val) {
CalcEntry(t,1.0,dt,tmp_val,old_val,false);
RHside_tmp = RHside;
RHside_tmp*=hRHsideTime(t);
tmp_val.add(dt, RHside_tmp);
old_val=tmp_val;
}
void step11::CPUDriver::ImplEulerStep(MyVector &old_val) {
RHside_tmp = RHside;
RHside_tmp*=(dt*hRHsideTime(t+dt));
RHside_tmp+=old_val;
GaussSeidel(t+dt,-dt,old_val,RHside_tmp,3);
}
void step11::CPUDriver::TrapezoidalStep(MyVector &old_val) {
CalcEntry(t,1.0,dt/2,tmp_val,old_val,false);
RHside_tmp = RHside;
RHside_tmp*=hRHsideTime(t);
tmp_val.add(dt/2.0, RHside_tmp);
RHside_tmp = RHside;
RHside_tmp*=hRHsideTime(t+dt);
tmp_val.add(dt/2.0, RHside_tmp);
GaussSeidel(t+dt,-dt/2,old_val,tmp_val,3);
}
void step11::CPUDriver::RungeKuttaStep(MyVector &old_val, int stage) {
int size= old_val.size();
MyVector k(size*stage);
int i, m, entry;
MyVector sum(size);
for (i=0; i<stage; i++) {
sum.reinit(size);
for (entry=0; entry<size; entry++) {
for (m=0; m<i; m++) {
sum(entry) += getRK_A(i,m,stage)*k(m*size+entry);
}
}
sum*=dt;
sum+=old_val;
CalcEntry(t+dt*getRK_c(i,stage), 0.0, 1.0, tmp_val, sum, false);
RHside_tmp = RHside;
RHside_tmp*=hRHsideTime(t+dt*getRK_c(i,stage));
tmp_val+=RHside_tmp;
for (entry=0; entry<size; entry++) {
k(i*size+entry)=tmp_val(entry);
}
}
MyVector bTIMESk;
bTIMESk.reinit(size);
for (i=0; i<size; i++) {
for (m=0; m<stage; m++) {
bTIMESk(i) += k(m*size+i)*getRK_b(m,stage);
}
}
bTIMESk *= dt;
old_val+=bTIMESk;
}
void step11::CPUDriver::ODESolve(double T, MyVector &old_val, MyVector &new_val, int solver) {
std::cout << "CPU-ODE-Solver v. 0.5 (Codename Komsomol): dt=" << dt << ", T=" << T << std::endl;
new_val=old_val;
while (t<T) {
switch (solver) {
case ODE_EULER:
EulerStep(new_val);
break;
case ODE_TRAP:
TrapezoidalStep(new_val);
break;
case ODE_RK:
RungeKuttaStep(new_val, 4);
break;
case ODE_IMPL_EULER:
ImplEulerStep(new_val);
break;
/ * case ODE_TRAP_STABLE:
if ( count_t==200 ) {
count_t=0;
}
else {
hTrapezoidalStep(t,dt,new_val);
count_t++;
}
break;
* /
}
t+=dt;
}
}
void step11::CPUDriver::CalcEntry(double _t, double eta, double lambda, MyVector &dest, MyVector &src, bool nondiag) {
int n1,n2,k1,k2;
int max_n1,min_n1,max_n2,min_n2;
std::complex<double> sum;
int pos1,pos2;
MyVector x_tmp((2*N+1)*(2*N+1));
for (k1=-N; k1<=N; k1++) {
max_n1=std::min(k1+N,n);
min_n1=std::max(k1-N,-n);
for (k2=-N; k2<=N; k2++) {
sum=0.0;
max_n2=std::min(k2+N,n);
min_n2=std::max(k2-N,-n);
for (n1=min_n1; n1<=max_n1; n1++) {
pos1=hGetVecPos(n1,min_n2,N);
pos2=hGetVecPos(k1-n1,k2-min_n2,N);
for (n2=min_n2; n2<=max_n2; n2++) {
sum-=std::complex<double>( ((k1-n1)*std::real(aX(pos1))+(k2-n2)*std::real(aY(pos1)))*std::real(src(pos2))-((k1-n1)*std::imag(aX(pos1))+(k2-n2)*std::imag(aY(pos1)))*std::imag(src(pos2)),((k1-n1)*std::real(aX(pos1))+(k2-n2)*std::real(aY(pos1)))*std::imag(src(pos2))+((k1-n1)*std::imag(aX(pos1))+(k2-n2)*std::imag(aY(pos1)))*std::real(src(pos2)) );
pos1++;
pos2--;
}
}
sum*=(std::complex<double>(0.0,1.0)*hATime(_t));
if (!nondiag) {
sum-=nu*(k1*k1+k2*k2)*src(hGetVecPos(k1,k2,N));
x_tmp(hGetVecPos(k1,k2,N)) = eta*src(hGetVecPos(k1,k2,N))+lambda*sum;
}
else {
sum+=std::complex<double>(0.0,1.0)* ((double)k1*aX(hGetVecPos(0,0,N))+(double)k2*aY(hGetVecPos(0,0,N))) * src(hGetVecPos(k1,k2,N)) * hATime(_t);
x_tmp(hGetVecPos(k1,k2,N)) = lambda*sum;
}
}
}
dest=x_tmp;
}
void step11::CPUDriver::GaussSeidel(double _t, double lambda, MyVector &result, MyVector &y, int iterations) {
unsigned int size=y.size();
assert(result.size()==size);
assert(size==(unsigned int)(2*N+1)*(2*N+1));
MyVector x_tmp((2*N+1)*(2*N+1));
std::complex<double> tmp;
result=y;
for (int k=0; k<iterations; k++) {
CalcEntry(_t,1.0,lambda,x_tmp,result,true);
result=y;
result-=x_tmp;
int pos=0;
for (int k1=-N; k1<=N; k1++) {
for (int k2=-N; k2<=N; k2++) {
tmp=nu*(k1*k1+k2*k2)+std::complex<double>(0.0,1.0)* ((double)k1*aX(hGetVecPos(0,0,N))+(double)k2*aY(hGetVecPos(0,0,N))) * hATime(_t);
result(hGetVecPos(k1,k2,N))/=(1.0-lambda*tmp);
pos++;
}
}
}
}
#endif
#ifndef CUDADriver_STEP_11_H
#define CUDADriver_STEP_11_H
#include <lac/blas++.h>
#include <string>
namespace step11 {
#include "cuda_driver_tools_step-11.h"
typedef blas_pp<ComplexNumber, cublas>::Vector FFTVectorBase;
class FFTVector : public FFTVectorBase {
public:
typedef FFTVectorBase Base;
FFTVector() {}
FFTVector(int nElements) : Base(nElements) {}
void print();
void setVal(int k, double x, double y) {
ComplexNumber tmp;
tmp.x=x;
tmp.y=y;
set(k,tmp);
}
void zeroVec();
};
class CUDADriver {
public:
typedef FFTVector MyVector;
CUDADriver() {
timer=0;
}
~CUDADriver ();
void init(int _N, int n, double _nu, int _solver, double _dt, std::vector<std::complex<double> > &_init_val, std::vector<std::complex<double> > &_aX, std::vector<std::complex<double> > &_aY, std::vector<std::complex<double> > &_RHside);
void run(double T);
void fetch(std::vector<std::complex<double> > &_result);
void EulerStep(MyVector &old_val);
void ImplEulerStep(MyVector &old_val);
void TrapezoidalStep(MyVector &old_val);
void RungeKuttaStep(MyVector &old_val, int stage);
void ODESolve(double T, MyVector &old_val, MyVector &new_val, int solver);
void dCalcMatProd(MyVector &result, MyVector &rhs, double lambda, double eta, double t, bool nondiag=false);
void dSolveGS(FFTVector &result, MyVector &rhs, double lambda, double t, int iterations);
double used_time;
private:
MyVector tmp_val;
MyVector init_val;
MyVector new_val;
MyVector aX;
MyVector aY;
MyVector RHside;
MyVector RHside_tmp;
MyVector RK_k;
MyVector sum;
unsigned int timer;
double t;
int N;
double nu;
double dt;
int solver;
};
} // namespace step11 END
#endif // CUDADriver_STEP_11_H
#ifndef CUDA_DRIVER_STEP_11_HH
#define CUDA_DRIVER_STEP_11_HH
#include "cuda_driver_step-11.h"
#include "cuda_kernel_wrapper_step-11.cu.h"
#include "tools_step-11.h"
#include <cutil_inline.h>
#include <fstream>
#include <cufft.h>
void step11::FFTVector::print() {
std::vector<ComplexNumber> tmp(this->__n);
ComplexNumber * dst_ptr = &tmp[0];
const ComplexNumber * src_ptr = this->val();
blas_wrapper_type::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
for (int i = 0; i < this->__n; ++i)
std::cout << "(" << tmp[i].x << "," << tmp[i].y << ")" << std::endl;
}
void step11::FFTVector::zeroVec() {
for (int i = 0; i < this->__n; i++) {
this->setVal(i,0.0,0.0);
}
}
step11::CUDADriver::~CUDADriver()
{
if (timer) {
CUT_SAFE_CALL(cutDeleteTimer(timer));
}
}
void step11::CUDADriver::init(int _N, int n, double _nu, int _solver, double _dt, std::vector<std::complex<double> > &_init_val, std::vector<std::complex<double> > &_aX, std::vector<std::complex<double> > &_aY, std::vector<std::complex<double> > &_RHside)
{
int k;
N=_N;
nu=_nu;
solver=_solver;
dt=_dt;
t=0.0;
used_time=0.0;
setParams(N,n,nu);
int size=(2*N+1)*(2*N+1)*sizeof(ComplexNumber);
init_val.reinit((2*N+1)*(2*N+1));
new_val.reinit((2*N+1)*(2*N+1));
tmp_val.reinit((2*N+1)*(2*N+1));
aX.reinit((2*N+1)*(2*N+1));
aX.zeroVec();
aY.reinit((2*N+1)*(2*N+1));
aY.zeroVec();
RHside.reinit((2*N+1)*(2*N+1));
RHside.zeroVec();
RK_k.reinit((2*N+1)*(2*N+1)*4);
sum.reinit((2*N+1)*(2*N+1));
for (k=0; k<init_val.size(); k++) {
init_val.setVal(k,std::real(_init_val[k]), std::imag(_init_val[k]));
}
for (k=0; k<aX.size(); k++) {
aX.setVal(k, std::real(_aX[k]), std::imag(_aX[k]));
aY.setVal(k, std::real(_aY[k]), std::imag(_aY[k]));
}
for (k=0; k<RHside.size(); k++) {
RHside.setVal(k, std::real(_RHside[k]), std::imag(_RHside[k]));
}
new_val=init_val;
if (timer) {
CUT_SAFE_CALL(cutDeleteTimer(timer));
}
CUT_SAFE_CALL(cutCreateTimer(&timer));
}
void step11::CUDADriver::run(double T) {
CUT_SAFE_CALL(cutStartTimer(timer));
ODESolve(t+T,new_val,new_val,solver);
CUT_SAFE_CALL(cutStopTimer(timer));
printf( "Processing time: %f (ms)\n", cutGetTimerValue(timer));
used_time=cutGetTimerValue(timer);
}
void step11::CUDADriver::fetch(std::vector<std::complex<double> > &result) {
assert(aX.size()==new_val.size());
int k;
for (k=0; k<new_val.size(); k++){
result[k]=std::complex<double>(new_val(k).x,new_val(k).y);
}
}
void step11::CUDADriver::EulerStep(MyVector &old_val) {
dCalcMatProd(tmp_val,old_val,dt,1.0,t);
RHside_tmp = RHside;
RHside_tmp*=(dt*dRHsideTime(t));
tmp_val+=RHside_tmp;
old_val=tmp_val;
}
void step11::CUDADriver::ImplEulerStep(MyVector &old_val) {
RHside_tmp = RHside;
RHside_tmp*=(dt*dRHsideTime(t+dt));
RHside_tmp+=old_val;
dSolveGS(old_val,RHside_tmp,-dt,t+dt,3);
}
void step11::CUDADriver::TrapezoidalStep(MyVector &old_val) {
dCalcMatProd(tmp_val,old_val,dt/2.0, 1.0,t);
RHside_tmp = RHside;
RHside_tmp*= (dt/2.0*dRHsideTime(t));
tmp_val+=RHside_tmp;
RHside_tmp = RHside;
RHside_tmp*=(dt/2.0*dRHsideTime(t+dt));
tmp_val+=RHside_tmp;
dSolveGS(old_val,tmp_val,-dt/2,t+dt, 3);
}
void step11::CUDADriver::RungeKuttaStep(MyVector &old_val, int stage) {
int i;
for (i=0; i<stage; i++) {
step_11_calcRKSumDummy(sum.array().val(),RK_k.array().val(),old_val.array().val(),dt,i,stage,N);
dCalcMatProd(tmp_val,sum,1.0,0.0,t+dt*getRK_c(i,stage),false);
RHside_tmp = RHside;
RHside_tmp*=dRHsideTime(t+dt*getRK_c(i,stage));
tmp_val+=RHside_tmp;
step_11_update_kDummy(tmp_val.array().val(),RK_k.array().val(),i,N);
}
step_11_update_valDummy(old_val.array().val(),RK_k.array().val(),dt,stage,N);
}
void step11::CUDADriver::ODESolve(double T, MyVector &old_val, MyVector &new_val, int solver) {
std::cout << "GPU-ODE-Solver v. 0.5 (Codename Komsomol): dt=" << dt << ", T=" << T << std::endl;
new_val=old_val;
while (t<T) {
switch (solver) {
case ODE_EULER:
EulerStep(new_val);
break;
case ODE_TRAP:
TrapezoidalStep(new_val);
break;
case ODE_RK:
RungeKuttaStep(new_val, 4);
break;
case ODE_IMPL_EULER:
ImplEulerStep(new_val);
break;
}
t+=dt;
}
}
void step11::CUDADriver::dCalcMatProd(MyVector &result, MyVector &rhs, double lambda, double eta, double t, bool nondiag) {
step_11_MatMultDummy(result.array().val(), aX.array().val(), aY.array().val(), rhs.array().val(), N, t, lambda, eta, nondiag);
}
void step11::CUDADriver::dSolveGS(MyVector &result, MyVector &rhs, double lambda, double t, int iterations) {
unsigned int size=rhs.size();
assert((unsigned)rhs.size()==size);
assert(size==(unsigned int)(2*N+1)*(2*N+1));
FFTVector x_tmp((2*N+1)*(2*N+1));
result=rhs;
for (int k=0; k<iterations; k++) {
x_tmp=result;
step_11_GaussSeidelDummy(result.array().val(), aX.array().val(), aY.array().val(), x_tmp.array().val(), rhs.array().val(), N, t, lambda);
}
}
/ *void step11::CUDADriver::testFFT() {
int NX=16;
int size=NX*sizeof(cuDoubleComplex);
cufftHandle plan;
cufftDoubleComplex *h_data1, *h_data2, *d_data1, *d_data2;
h_data1 = (cuDoubleComplex*)malloc(size);
h_data2 = (cuDoubleComplex*)malloc(size);
cudaMalloc( (void**)&d_data1, size );
cudaMalloc( (void**)&d_data2, size );
for(int i=0; i< NX; i++) {
h_data1[i].x = cos(2*M_PI*i/NX);
h_data1[i].y = 0.0;
}
cudaMemcpy(d_data1, h_data1, size, cudaMemcpyHostToDevice);
cufftPlan1d( &plan, NX, CUFFT_Z2Z, 1);
cufftExecZ2Z(plan, d_data1, d_data2, CUFFT_FORWARD );
cudaMemcpy(h_data2, d_data2, size, cudaMemcpyDeviceToHost);
cufftDestroy(plan);
cudaFree(d_data1);
cudaFree(d_data2);
for(int i = 0 ; i < NX ; i++){
printf("dataHost[%d] %f %f\n", i, h_data1[i].x, h_data1[i].y);
printf("data[%d] %f %f\n\n", i, h_data2[i].x, h_data2[i].y);
}
}* /
#endif // CUDA_DRIVER_STEP_11_HH
#ifndef CUDA_KERNEL_STEP_11_CU_H
#define CUDA_KERNEL_STEP_11_CU_H
void setParams(int __N, int __n, double __nu);
void step_11_MatMultDummy(cuDoubleComplex *result, cuDoubleComplex *aX, cuDoubleComplex *aY, cuDoubleComplex *input, int N, double t, double lambda, double eta, bool nondiag);
void step_11_GaussSeidelDummy(cuDoubleComplex *result, cuDoubleComplex *aX, cuDoubleComplex *aY, cuDoubleComplex *input, cuDoubleComplex *rhside, int N, double t, double lambda);
void step_11_calcRKSumDummy(cuDoubleComplex *partialSum, cuDoubleComplex *k, cuDoubleComplex *y, double dt, int m, int stage, int N);
void step_11_update_kDummy(cuDoubleComplex *partialSum, cuDoubleComplex *k, int m, int N);
void step_11_update_valDummy(cuDoubleComplex *result, cuDoubleComplex *k, double dt, int stage, int N);
#endif // CUDA_KERNEL_STEP_11_CU_H
#include <cutil_inline.h>
#include <cuda_kernel_wrapper_step-11.cu.h>
#include "cuda_driver_tools_step-11.h"
__constant__ double d_nu;
__constant__ int d_N;
__constant__ int d_n;
void setParams(int __N, int __n, double __nu)
{
CUDA_SAFE_CALL(cudaMemcpyToSymbol("d_nu", (void**)&__nu, sizeof(__nu)));
CUDA_SAFE_CALL(cudaMemcpyToSymbol("d_N", (void**)&__N, sizeof(__N)));
CUDA_SAFE_CALL(cudaMemcpyToSymbol("d_n", (void**)&__n, sizeof(__n)));
}
__device__ ComplexNumber dCalcConv(ComplexNumber *aX, ComplexNumber *aY, ComplexNumber *src, int N, double t) {
int n1,n2,k1,k2;
int max_n1,min_n1,max_n2,min_n2;
ComplexNumber sum;
int pos1,pos2;
k1 = blockIdx.x*blockDim.x+threadIdx.x-N;
k2 = blockIdx.y*blockDim.y+threadIdx.y-N;
sum.x=0.0;
sum.y=0.0;
max_n1=dMin(k1+N,d_n);
min_n1=dMax(k1-N,-d_n);
max_n2=dMin(k2+N,d_n);
min_n2=dMax(k2-N,-d_n);
for (n1=min_n1; n1<=max_n1; n1++) {
pos1=dGetVecPos(n1,min_n2,N);
pos2=dGetVecPos(k1-n1,k2-min_n2,N);
for (n2=min_n2; n2<=max_n2; n2++) {
sum-=((k1-n1)*aX[pos1]+(k2-n2)*aY[pos1])*src[pos2];
pos1++;
pos2--;
}
}
sum*=(ImUnit()*dATime(t));
return sum;
}
__global__ void __calcEntryThread(ComplexNumber *dest, ComplexNumber *aX, ComplexNumber *aY, ComplexNumber *src, double t, double lambda, double eta) {
ComplexNumber sum;
int k1 = blockIdx.x*blockDim.x+threadIdx.x-d_N;
int k2 = blockIdx.y*blockDim.y+threadIdx.y-d_N;
if ( (k1>d_N) || (k2>d_N) )
return;
sum = dCalcConv(aX, aY, src, d_N, t);
sum-=d_nu*((double)(k1*k1+k2*k2))*src[dGetVecPos(k1,k2,d_N)];
dest[dGetVecPos(k1,k2,d_N)] = eta*src[dGetVecPos(k1,k2,d_N)]+lambda*sum;
}
__global__ void __calcEntryThreadNonDiag(ComplexNumber *dest, ComplexNumber *aX, ComplexNumber *aY, ComplexNumber *src, double t, double lambda) {
ComplexNumber sum;
int k1 = blockIdx.x*blockDim.x+threadIdx.x-d_N;
int k2 = blockIdx.y*blockDim.y+threadIdx.y-d_N;
if ( (k1>d_N) || (k2>d_N) ){
return;
}
sum = dCalcConv(aX, aY, src, d_N, t);
sum+=((double) k1*aX[dGetVecPos(0,0,d_N)]+(double) k2*aY[dGetVecPos(0,0,d_N)]) * ImUnit() * src[dGetVecPos(k1,k2,d_N)] * dATime(t);
dest[dGetVecPos(k1,k2,d_N)] = lambda*sum;
}
__global__ void __calcGaussSeidelThread(ComplexNumber *dest, ComplexNumber *aX, ComplexNumber *aY, ComplexNumber *src, ComplexNumber *rhside, double t, double lambda) {
int k1,k2;
ComplexNumber tmp;
ComplexNumber sum;
k1 = blockIdx.x*blockDim.x+threadIdx.x-d_N;
k2 = blockIdx.y*blockDim.y+threadIdx.y-d_N;
if ( (k1>d_N) || (k2>d_N) ){
return;
}
sum = dCalcConv(aX, aY, src, d_N, t);
sum+=((double) k1*aX[dGetVecPos(0,0,d_N)]+(double) k2*aY[dGetVecPos(0,0,d_N)]) * ImUnit() * src[dGetVecPos(k1,k2,d_N)]*dATime(t);
sum = lambda*sum;
sum = rhside[dGetVecPos(k1,k2,d_N)] - sum;
tmp=d_nu*(k1*k1+k2*k2) + ( ((double) k1*aX[dGetVecPos(0,0,d_N)]+(double) k2*aY[dGetVecPos(0,0,d_N)])*ImUnit()*dATime(t));
dest[dGetVecPos(k1,k2,d_N)] = sum/( 1.0+ ((-1.0)*lambda*tmp) );
}
__global__ void __calcRKSum(ComplexNumber *partialSum, ComplexNumber *k, ComplexNumber *y, double dt, int m, int stage) {
int k1,k2,i;
k1 = blockIdx.x*blockDim.x+threadIdx.x-d_N;
k2 = blockIdx.y*blockDim.y+threadIdx.y-d_N;
if ( (k1>d_N) || (k2>d_N) ){
return;
}
int size=(2*d_N+1)*(2*d_N+1);
ComplexNumber sum;
sum.x=0.0;
sum.y=0.0;
ComplexNumber tmp;
for (i=0; i<m; i++) {
tmp = dGetRK_A(m,i,stage)*k[i*size+dGetVecPos(k1,k2,d_N)];
sum += tmp;
}
sum=dt*sum;
sum+=y[dGetVecPos(k1,k2,d_N)];
partialSum[dGetVecPos(k1,k2,d_N)] = sum;
}
__global__ void __update_k(ComplexNumber *partialSum, ComplexNumber *k, int m) {
int k1,k2;
k1 = blockIdx.x*blockDim.x+threadIdx.x-d_N;
k2 = blockIdx.y*blockDim.y+threadIdx.y-d_N;
if ( (k1>d_N) || (k2>d_N) ){
return;
}
int size=(2*d_N+1)*(2*d_N+1);
k[m*size+dGetVecPos(k1,k2,d_N)] = partialSum[dGetVecPos(k1,k2,d_N)];
}
__global__ void __update_val(ComplexNumber *result, ComplexNumber *k, double dt, int stage) {
int k1,k2,i;
k1 = blockIdx.x*blockDim.x+threadIdx.x-d_N;
k2 = blockIdx.y*blockDim.y+threadIdx.y-d_N;
if ( (k1>d_N) || (k2>d_N) ){
return;
}
int size=(2*d_N+1)*(2*d_N+1);
ComplexNumber sum;
sum.x=0.0;
sum.y=0.0;
for (i=0; i<stage; i++) {
sum=sum+dGetRK_b(i,stage)*k[i*size+dGetVecPos(k1,k2,d_N)];
}
result[dGetVecPos(k1,k2,d_N)] += dt*sum;
}
void step_11_MatMultDummy(ComplexNumber *result, ComplexNumber *aX, ComplexNumber *aY, ComplexNumber *input, int N, double t, double lambda, double eta, bool nondiag)
{
dim3 grid;
dim3 blocks;
calcCudaParams(grid,blocks,N);
if (nondiag)
__calcEntryThreadNonDiag<<<grid, blocks>>>(result, aX, aY, input, t, lambda);
else
__calcEntryThread<<<grid, blocks>>>(result, aX, aY, input, t, lambda, eta);
cudaThreadSynchronize();
}
void step_11_GaussSeidelDummy(ComplexNumber *result, ComplexNumber *aX, ComplexNumber *aY, ComplexNumber *input, ComplexNumber *rhside, int N, double t, double lambda)
{
dim3 grid;
dim3 blocks;
calcCudaParams(grid,blocks,N);
__calcGaussSeidelThread<<<grid, blocks>>>(result, aX, aY, input, rhside, t, lambda);
cudaThreadSynchronize();
}
void step_11_calcRKSumDummy(ComplexNumber *partialSum, ComplexNumber *k, ComplexNumber *y, double dt, int m, int stage, int N) {
dim3 grid;
dim3 blocks;
calcCudaParams(grid,blocks,N);
__calcRKSum<<<grid, blocks>>>(partialSum, k, y, dt, m, stage);
cudaThreadSynchronize();
}
void step_11_update_kDummy(ComplexNumber *partialSum, ComplexNumber *k, int m, int N) {
dim3 grid;
dim3 blocks;
calcCudaParams(grid,blocks,N);
__update_k<<<grid, blocks>>>(partialSum, k, m);
cudaThreadSynchronize();
}
void step_11_update_valDummy(ComplexNumber *result, ComplexNumber *k, double dt, int stage, int N) {
dim3 grid;
dim3 blocks;
calcCudaParams(grid,blocks,N);
__update_val<<<grid, blocks>>>(result, k, dt, stage);
cudaThreadSynchronize();
}
#include <iostream>
#include <vector>
#include <math.h>
#include "cuda_driver_step-11.h"
#include "cpu_driver_step-11.h"
#include <lac/vector.h>
#include <lac/blas++.h>
#include "cuda_driver_step-11.hh"
#include "cpu_driver_step-11.hh"
#include "cuda_driver_tools_step-11.h"
#include "fancy_vector.h"
#include "fancy_vector.hh"
#define USE_DEAL_II
#undef USE_DEAL_II
using namespace step11;
namespace step11 {
class MyFancySimulation {
public:
MyFancySimulation();
void run();
private:
void save(double t, std::string name);
void getRHSorA(std::vector<std::complex<double> > &_RHside, double(step11::MyFancySimulation::*f)(double,double));
inline double originalRHS(double x, double y);
inline double originalAX(double x, double y);
inline double originalAY(double x, double y);
void dFFT(int NX, int NY, cufftDoubleComplex *h_dataIn, cufftDoubleComplex *h_dataOut, bool inverse=false);
void sortVecFFT(cufftDoubleComplex *h_dataIn, int size);
int hSelftest();
double calcError(std::vector<std::complex<double> > &result, double T);
CUDADriver cudaDriver;
CPUDriver cpuDriver;
std::vector<std::complex<double> > result;
int N,n;
double nu;
int solver;
double T;
double dt;
};
}
step11::MyFancySimulation::MyFancySimulation()
{
}
inline double step11::MyFancySimulation::originalRHS(double x, double y) {
return cos(x+y);
}
inline double step11::MyFancySimulation::originalAX(double x, double y) {
return 1.0;
}
inline double step11::MyFancySimulation::originalAY(double x, double y) {
return 1.0;
}
void step11::MyFancySimulation::getRHSorA(std::vector<std::complex<double> > &_RHside, double(step11::MyFancySimulation::*f)(double,double)) {
assert(_RHside.size()==(unsigned int)(2*N+1)*(2*N+1));
int size=(2*N+1)*(2*N+1)*sizeof(ComplexNumber);
int i, j;
for (j=0; j< (2*N+1); j++) {
for (i=0; i< (2*N+1); i++) {
_RHside[j*(2*N+1)+i]= (*this.*f)(2.0*M_PI*i/(2*N+1), 2.0*M_PI*j/(2*N+1));
}
}
cufftDoubleComplex *FFT_RHside;
FFT_RHside = (cuDoubleComplex*)malloc(size);
for (i=0; i<(2*N+1)*(2*N+1); i++) {
FFT_RHside[i].x = std::real(_RHside[i]);
FFT_RHside[i].y = std::imag(_RHside[i]);
}
dFFT(2*N+1, 2*N+1, FFT_RHside, FFT_RHside, false);
for (i=0; i<(2*N+1)*(2*N+1); i++) {
_RHside[i] = std::complex<double>(FFT_RHside[i].x,FFT_RHside[i].y);
}
free(FFT_RHside);
}
void step11::MyFancySimulation::run() {
hSelftest();
return;
int k1,k2;
N=5;
n=5;
nu=0.1;
T=0.01;
dt=1e-4;
solver=ODE_TRAP;
double t=0.0;
double delta_t=0.1;
std::vector<std::complex<double> > aX((2*N+1)*(2*N+1));
std::vector<std::complex<double> > aY((2*N+1)*(2*N+1));
std::vector<std::complex<double> > RHside((2*N+1)*(2*N+1));
std::vector<std::complex<double> > initVal((2*N+1)*(2*N+1));
result.resize((2*N+1)*(2*N+1));
for (k1=-N; k1<=N; k1++) {
for (k2=-N; k2<=N; k2++) {
aX[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
aY[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
RHside[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
initVal[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
}
}
/ * cudaDriver.init(N, n, nu, solver, dt, initVal, a, RHside);
cudaDriver.fetch(result);
save(t, "data/test");
while (t<T) {
cudaDriver.run(delta_t);
cudaDriver.fetch(result);
save(t, "data/test");
std::cout << result[hGetVecPos(1,2,N)] << std::endl;
t+=delta_t;
}
* /
std::cout << "init GPU..." << std::endl;
cudaDriver.init(N, n, nu, solver, dt, initVal, aX, aY, RHside);
cudaDriver.run(T,solver);
cudaDriver.fetch(result);
std::cout << result[hGetVecPos(1,2,N)] << std::endl;
/ *cpuDriver.init(N, n, nu, solver, dt, initVal, aX, aY, RHside);
cpuDriver.run(T);
cpuDriver.fetch(result);
std::cout << result[hGetVecPos(1,2,N)] << std::endl;* /
return;
}
void step11::MyFancySimulation::save(double t, std::string name) {
int size=(2*N+1)*(2*N+1)*sizeof(ComplexNumber);
int i,k,k1,k2;
double x, y, u_norm;
cufftDoubleComplex *uX, *uY;
uX = (cuDoubleComplex*)malloc(size);
uY = (cuDoubleComplex*)malloc(size);
for (k1=-N; k1<=N; k1++) {
for (k2=-N; k2<=N; k2++) {
uX[hGetVecPos(k1,k2,N)].x = std::real(result[hGetVecPos(k1,k2,N)]);
uX[hGetVecPos(k1,k2,N)].y = std::imag(result[hGetVecPos(k1,k2,N)]);
uY[hGetVecPos(k1,k2,N)] = uX[hGetVecPos(k1,k2,N)];
uX[hGetVecPos(k1,k2,N)]*= ((double)k2)/(k1*k1+k2*k2)*ImUnit();
uY[hGetVecPos(k1,k2,N)]*= -((double)k1)/(k1*k1+k2*k2)*ImUnit();
}
}
uX[hGetVecPos(0,0,N)]=0.0*ImUnit();
uY[hGetVecPos(0,0,N)]=0.0*ImUnit();
sortVecFFT(uX, size);
sortVecFFT(uY, size);
dFFT(2*N+1, 2*N+1, uX, uX, true);
dFFT(2*N+1, 2*N+1, uY, uY, true);
std::ostringstream filename;
filename << name << t << ".dat";
std::ofstream f;
f.open(filename.str().c_str(), std::ios::out);
for (i=0; i<2*N+1; i++) {
for (k=0; k<2*N+1; k++) {
x = 2.0*M_PI*i/(2*N+1);
y = 2.0*M_PI*k/(2*N+1);
u_norm = sqrt( uX[k*(2*N+1)+i].x* uX[k*(2*N+1)+i].x + uY[k*(2*N+1)+i].x* uY[k*(2*N+1)+i].x);
f << x << "\t" << y << "\t" << u_norm << std::endl;
}
f << std::endl;
}
f << std::endl;
f.close();
free(uX);
free(uY);
}
void step11::MyFancySimulation::sortVecFFT(cufftDoubleComplex *h_dataIn, int size){
ComplexNumber *tmp;
tmp = (ComplexNumber*)malloc(size);
cufftDoubleComplex *ordered;
ordered = (cuDoubleComplex*)malloc(size);
for(int i = 0 ; i < 2*N+1 ; i++){
for(int k=0; k<N; k++){
ordered[k+i*(2*N+1)+N+1] = h_dataIn[k+i*(2*N+1)];
ordered[k+i*(2*N+1)] = h_dataIn[k+i*(2*N+1)+N];
}
ordered[N+i*(2*N+1)] = h_dataIn[N+i*(2*N+1)+N];
}
memcpy(tmp,ordered,size);
for(int k = 0 ; k < 2*N+1 ; k++){
for(int i=0; i<N; i++){
ordered[k+(i+1)*(2*N+1)+N*(2*N+1)] = tmp[k+i*(2*N+1)];
ordered[k+i*(2*N+1)] = tmp[k+i*(2*N+1)+N*(2*N+1)];
}
ordered[k+N*(2*N+1)] = tmp[k+N*(2*N+1)+N*(2*N+1)];
}
memcpy(h_dataIn,ordered,size);
}
void step11::MyFancySimulation::dFFT(int NX, int NY, cufftDoubleComplex *h_dataIn, cufftDoubleComplex *h_dataOut, bool inverse) {
int size=NX*NY*sizeof(cuDoubleComplex);
cufftHandle plan;
cufftDoubleComplex *d_dataIn, *d_dataOut;
cudaMalloc( (void**)&d_dataIn, size );
cudaMalloc( (void**)&d_dataOut, size );
cudaMemcpy(d_dataIn, h_dataIn, size, cudaMemcpyHostToDevice);
cufftPlan2d( &plan, NX, NY, CUFFT_Z2Z);
if(!inverse) {
cufftExecZ2Z(plan, d_dataIn, d_dataOut, CUFFT_FORWARD );
}
else {
cufftExecZ2Z(plan, d_dataIn, d_dataOut, CUFFT_INVERSE );
}
cudaThreadSynchronize();
cudaMemcpy(h_dataOut, d_dataOut, size, cudaMemcpyDeviceToHost);
cufftDestroy(plan);
cudaFree(d_dataIn);
cudaFree(d_dataOut);
if(inverse) {
for(int i = 0 ; i < NX*NY ; i++){
h_dataOut[i] = 1.0/(NX*NY) *h_dataOut[i];
}
}
}
int MyFancySimulation::hSelftest() {
int k1,k2,i,j,k,num_iter;
N=20;
n=20;
nu=0.1;
T=0.1;
dt=1e-3;
solver=ODE_RK;
std::vector<std::complex<double> > aX((2*N+1)*(2*N+1));
std::vector<std::complex<double> > aY((2*N+1)*(2*N+1));
std::vector<std::complex<double> > RHside((2*N+1)*(2*N+1));
std::vector<std::complex<double> > initVal((2*N+1)*(2*N+1));
result.resize((2*N+1)*(2*N+1));
/ * for (k1=-N; k1<=N; k1++) {
for (k2=-N; k2<=N; k2++) {
aX[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
aY[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
RHside[hGetVecPos(k1,k2,N)]=0.0;
int max_n1,min_n1,max_n2,min_n2;
max_n1=std::min(k1+N,n);
min_n1=std::max(k1-N,-n);
max_n2=std::min(k2+N,n);
min_n2=std::max(k2-N,-n);
for (int n1=min_n1; n1<=max_n1; n1++) {
for (int n2=min_n2; n2<=max_n2; n2++) {
RHside[hGetVecPos(k1,k2,N)]+=((double)(k1-n1+k2-n2)/( (((k1-n1)*(k1-n1))+1)*((k2-n2)*(k2-n2)+1)*(n1*n1+1)*(n2*n2+1)) );
}
}
RHside[hGetVecPos(k1,k2,N)]*=std::complex<double>(0.0,1.0);
RHside[hGetVecPos(k1,k2,N)]+=nu*(k1*k1+k2*k2-1)/((k1*k1+1)*(k2*k2+1));
initVal[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
}
}
double errorL2[4]={0.0,0.0,0.0,0.0};
std::ofstream f;
f.open("data/errors.dat", std::ios::out);
dt=1.0;
for (i=1; i<30; i++) {
dt=dt/2.0;
for (j=1; j<5; j++) {
solver=j;
cudaDriver.init(N, n, nu, solver, dt, initVal, aX, aY, RHside);
cudaDriver.run(T);
cudaDriver.fetch(result);
errorL2[j-1] = calcError(result,T);
}
f << dt << "\t" << errorL2[0] << "\t" << errorL2[1] << "\t" << errorL2[2] << "\t" << errorL2[3] << std::endl;
}
f.close();
* /
double times[8]={0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0};
double sigmas[8]={0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0};
double times_tmp[10];
std::ofstream f;
f.open("data/times.dat", std::ios::out | std::ios::app);
dt=1e-4;
T=0.01;
N=34;
num_iter=10;
CUDADriver *cudaDriver_tmp;
for (i=1; i<30; i++) {
N+=2;
n=N;
std::cout << std::endl << "N=" << N << std::endl;
aX.resize((2*N+1)*(2*N+1));
aY.resize((2*N+1)*(2*N+1));
RHside.resize((2*N+1)*(2*N+1));
initVal.resize((2*N+1)*(2*N+1));
result.resize((2*N+1)*(2*N+1));
for (k1=-N; k1<=N; k1++) {
for (k2=-N; k2<=N; k2++) {
aX[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
aY[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
RHside[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
initVal[hGetVecPos(k1,k2,N)]=1.0/((k1*k1+1)*(k2*k2+1));
}
}
cudaDriver.init(N, n, nu, solver, dt, initVal, aX, aY, RHside);
for (j=1; j<5; j++) {
solver=j;
std::cout << "GPU, solver=" << j << std::endl;
for (k=0; k<num_iter; k++) {
cudaDriver.reset(initVal);
cudaDriver.run(T,solver);
cudaDriver.fetch(result);
times[j-1] += cudaDriver.used_time;
times[k] = cudaDriver.used_time;
}
times[j-1]/=num_iter;
for (k=0; k<num_iter; k++) {
sigmas[j-1]+=((times_tmp[k]-times[j-1])*(times_tmp[k]-times[j-1]));
sigmas[j-1]=sqrt(sigmas[j-1]/(num_iter-1));
}
}
for (j=1; j<5; j++) {
solver=j;
std::cout << "CPU, solver=" << j << std::endl;
for (k=0; k<num_iter; k++) {
cpuDriver.init(N, n, nu, solver, dt, initVal, aX, aY, RHside);
cpuDriver.run(T);
times[4+j-1] += cpuDriver.used_time;
times_tmp[k] = cpuDriver.used_time;
}
times[4+j-1]/=num_iter;
for (k=0; k<num_iter; k++) {
sigmas[4+j-1]+=((times_tmp[k]-times[4+j-1])*(times_tmp[k]-times[4+j-1]));
sigmas[4+j-1]=sqrt(sigmas[4+j-1]/(num_iter-1));
}
}
f << N << "\t" << times[0] << "\t" << times[1] << "\t" << times[2] << "\t" << times[3] << "\t" << times[4] << "\t" << times[5] << "\t" << times[6] << "\t" << times[7] << "\t" << sigmas[0] << "\t" << sigmas[1] << "\t" << sigmas[2] << "\t" << sigmas[3] << "\t" << sigmas[4] << "\t" << sigmas[5] << "\t" << sigmas[6] << "\t" << sigmas[7] << std::endl;
}
f.close();
return true;
}
double MyFancySimulation::calcError(std::vector<std::complex<double> > &result, double T) {
double errorL2=0.0;
std::complex<double> error_tmp;
int k1,k2;
for (k1=-N; k1<=N; k1++) {
for (k2=-N; k2<=N; k2++) {
error_tmp = result[hGetVecPos(k1,k2,N)]-std::complex<double>(exp(-nu*T)*1.0/((k1*k1+1.0)*(k2*k2+1.0)), 0.0);
errorL2 += std::abs(error_tmp)*std::abs(error_tmp);
}
}
return(sqrt(errorL2));
}
int main(int / *argc* /, char * / *argv* /[])
{
using namespace step11;
MyFancySimulation machma;
machma.run();
}
 documentation generated on Mon Jul 18 12:05:08 2011 by
doxygen
1.5.7
documentation generated on Mon Jul 18 12:05:08 2011 by
doxygen
1.5.7