CUDA Lab Course Reference Manual 2011

The step-12 tutorial program

Table of contents
  1. Introduction
  2. The commented program
  1. Results
  2. The plain program

Introduction

Finite difference and multigrid methods for the Poisson-Boltzmann equation for accelerating Monte-Carlo simulations of simple models for protein folding. The intramolecular dynamics is simulated using the HP lattice model. The Poisson-Boltzmann equation models the energy constribution due to screening effects due to exterior counter ions.

Physical Model

We describe a protein as a bunch of point charges in some kind of insulator (fat).

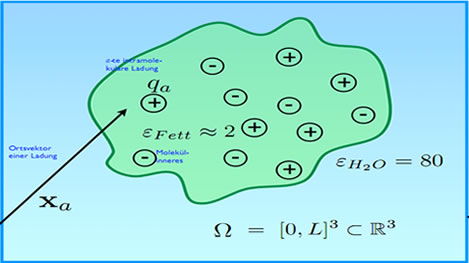
model1.jpg

Sketch of model

Mathematical model is the well known Poisson's equation

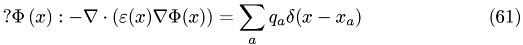
\begin{eqnarray}? \Phi \left ( x \right ):-\nabla \cdot ( \varepsilon (x) \nabla \Phi(x))= \sum_{a}{q_{a}}\delta(x-{x_{a}})\end{eqnarray}

The potential is denoted as 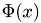$\Phi (x)$, permittivity by 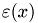$\varepsilon (x)$ and the intramolecular charge distribution is given by

\begin{eqnarray} \sum_a q_{a}\delta(x-x_{a})\end{eqnarray}

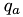where $q_{a}$ is a-th intramolecular charge and 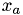$x_{a}$ is position of the charge.

Discretization of the Physical Model

Discretizing domain with a regular grid

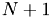$ N+1 $ - points per coordinate axis
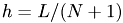$h = L / (N+1)$ - width of a cell
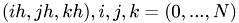$(ih, jh, kh), i,j,k = (0,...,N)$ - discretized coordinates within a domain
.

Approximation of the right-hand side of the equation

To discretize the 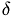$\delta$ -function we use

Given y is in the cell

\begin{eqnarray}\delta (x-y)=\begin{cases} & \text{ } \frac{1}{h^3}\: \: \: \: \: y\in [ih, ih+h]\times [jh,jh+h]\times[kh,kh+h]\\ & \text{ } 0 \:\: \: \: \: \: \: else \end{cases}\end{eqnarray}

=> discretized charge distribution

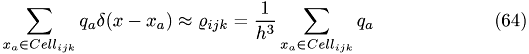
\begin{eqnarray}\sum_{x_{a}\in Cell_{ijk}} q_{a}\delta(x-x_{a}) \approx \varrho_{ijk} = \frac{1}{h^3}\sum_{x_{a}\in Cell_{ijk}} q_{a}\end{eqnarray}

Discretizing Laplacian

Let's denote the discrete potential as 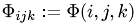$\Phi_{ijk} := \Phi(i,j,k)$

Approximations of the Laplacian, obtained by the finite difference methode are:

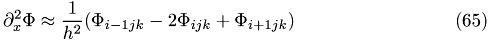
\begin{eqnarray}\partial^2_{x}\Phi\approx \frac{1}{h^2}(\Phi_{i-1jk}-2\Phi_{ijk}+\Phi_{i+1jk})\end{eqnarray}

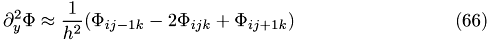
\begin{eqnarray}\partial^2_{y}\Phi\approx \frac{1}{h^2}(\Phi_{ij-1k}-2\Phi_{ijk}+\Phi_{ij+1k})\end{eqnarray}

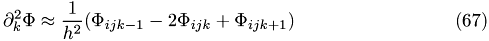
\begin{eqnarray}\partial^2_{k}\Phi\approx \frac{1}{h^2}(\Phi_{ijk-1}-2\Phi_{ijk}+\Phi_{ijk+1})\end{eqnarray}

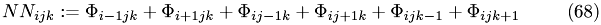
\begin{eqnarray} NN_{ijk} := \Phi_{i-1jk}+\Phi_{i+1jk}+\Phi_{ij-1k}+\Phi_{ij+1k}+\Phi_{ijk-1}+\Phi_{ijk+1} \end{eqnarray}

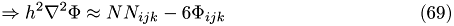
\begin{eqnarray} \Rightarrow h^2\nabla^2\Phi\approx NN_{ijk} - 6\Phi_{ijk} \end{eqnarray}

Resulting discretized Poisson's equation

\begin{eqnarray} -NN_{ijk}+6\Phi_{ijk} = h^2\varrho_{ijk}\end{eqnarray}

Extended Physical Model

The extended model adds nonlinear term to the origin Poisson's equation

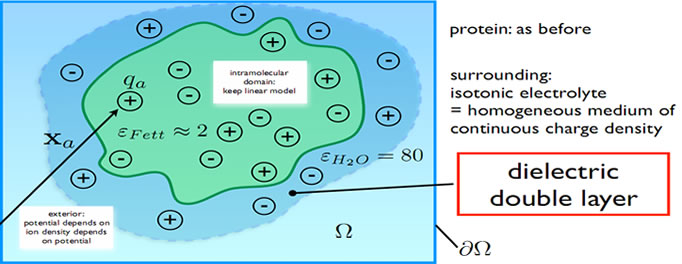
model1_extended.jpg

Sketch of model

Resulting equation follows from Debye-Hückel theory

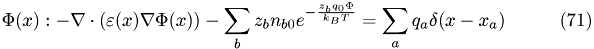
\begin{eqnarray} \Phi(x): -\nabla \cdot (\varepsilon(x)\nabla\Phi(x)) - \sum_{b} z_{b}n_{b0}e^{-\frac{z_{b}q_{0}\Phi}{k_{B}T}} = \sum_{a}q_{a}\delta(x-x_{a}) \end{eqnarray}

Solving Methods

Relaxation

Relaxation Methods are used to perform smoothing operations by Multgrid Methods. After dicretization we can represent our model as the equation 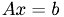$\textbf{}{Ax = b}$.

Relaxation methods make immediate use of the structure of the sparse matrix 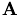$\mathbf{A}$

The Matrix 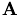$\mathbf{A}$ is split into two parts

\begin{eqnarray}\mathbf{A = E - F}\end{eqnarray}

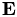where $\mathbf{E}$ is easily invertible an 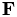$\mathbf{F}$ is the remainder.

then 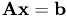$\mathbf{Ax = b}$ becomes

\begin{eqnarray}\mathbf{E\cdot x^{(r)} =F\cdot x^{(r-1)} + b }\end{eqnarray}

Jacobi and Gauss-Seidel

Consider splitting Matrix 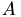$A$ as

\begin{eqnarray}\mathbf{A = L + D + U }\end{eqnarray}

For the Jacobi method the easily inertible part is given by

\begin{eqnarray}\mathbf{E} = \mathbf{D}\end{eqnarray}

and the remainder is

\begin{eqnarray}\mathbf{F} = \mathbf{-(L+D)} \end{eqnarray}

Gauß-Seidel Method we have

\begin{eqnarray}\mathbf{E} = \mathbf{L+D}\end{eqnarray}

\begin{eqnarray} \mathbf{F} = \mathbf{-U} \end{eqnarray}

Multigrid Methods

Practical multigrid methods can solve elliptic PDEs discretized on N grid points in O(N) operations. The multigrid methods can solve general elliptic equations with nonconstant coefficients with hardly any loss in efficiency. Even nonlinear equations can be solved with comparable speed.

Suppose we are trying to solve linear elliptic Problem (Poisson's equation)

\begin{eqnarray} \mathcal{L} u = f\end{eqnarray}

Discretize equation on a uniform grid with mesh size h

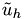\begin{eqnarray} \mathcal{L}_h \tilde u_{h} \approx f_{h}\end{eqnarray}

Let $ \tilde{u}_{h}$ denote some approximate solution
and 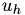$ {u}_{h}$ denote exact solution

The error is then

\begin{eqnarray} v_{h} = u_{h} -\tilde{u}_{h}\end{eqnarray}

The residual is

\begin{eqnarray} d_{h} = \mathcal{L}_{h}\tilde{u}_h - f_{h}\end{eqnarray}

In the next step we have to approximate the discretized operator

\begin{eqnarray} \mathcal{L}_{h}\end{eqnarray}

with

\begin{eqnarray} \mathcal{\hat L}_{h}\end{eqnarray}

and solve using one of a relaxation method described above (Jacobi or Gauß-Seidel)

\begin{eqnarray} ?\hat{v}_{h}: \mathcal{\hat L}_{h}\hat{v}_{h} = -d_{h}\end{eqnarray}

Then we get a new improved approximate solution

\begin{eqnarray} \tilde u_{h}^{new} = \tilde u_{h} +\hat v_{h}\end{eqnarray}

Full Algorithm

1. Pre-Smoothing (S)

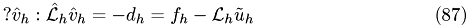
\begin{eqnarray} ?\hat v_{h} : \mathcal{\hat L}_{h}\hat v_{h} = -d_{h} = f_{h} - \mathcal{L}_{h}\tilde u_{h}\end{eqnarray}

with approximate solution

\begin{eqnarray} \tilde u_{h}\end{eqnarray}

improved initial solution:

\begin{eqnarray} \bar u_{h} = \tilde u_{h} +\hat v_{h}\end{eqnarray}

2. Coarse grid correction(C)

\begin{eqnarray} d_{H} = \mathcal R(\mathcal L_{h}\bar u_{h}-f_{h})\end{eqnarray}

restrict defect to coarse grid

\begin{eqnarray} \tilde v_{H} : \mathcal {L}_{H}\tilde v_{H} = -d_{H}\end{eqnarray}

correction on coarse grid

\begin{eqnarray}\tilde u_{h} = \bar u_{h} +\mathcal P\tilde v_{H}\end{eqnarray}

add correction from coarse grid to fine-grid solution

3. Post-Smoothing (P)

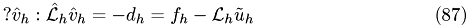
\begin{eqnarray} ?\hat v_{h} : \mathcal{\hat L}_{h}\hat v_{h} = -d_{h} = f_{h} - \mathcal{L}_{h}\tilde u_{h}\end{eqnarray}

\begin{eqnarray} \bar u_{h} = \tilde u_{h} +\hat v_{h}\end{eqnarray}

where

\begin{eqnarray} \mathcal R\end{eqnarray}

is the restriction operator and

\begin{eqnarray} \mathcal P\end{eqnarray}

is the prolongation operator.

Multigrid Cycles

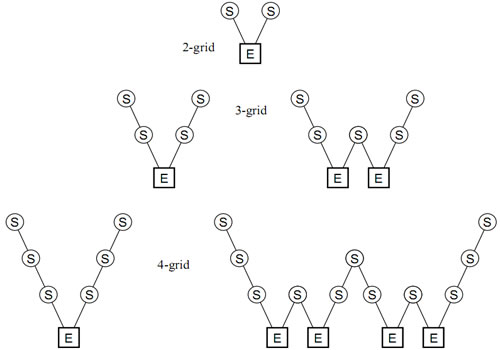
MG_cycles.jpg

Full Multigrid Cycles

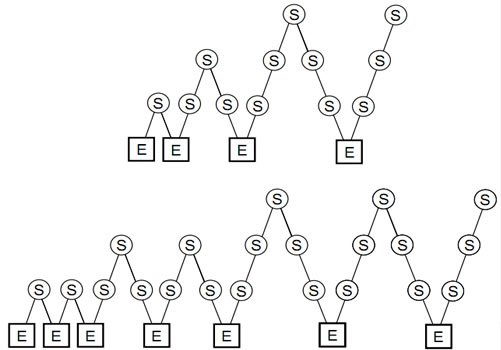
FMG_cycles.jpg

In figures above:
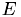$E$ - denotes excact solution
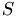$S$ - denotes smoothing operation

The main difference between Multigrid Cycles and Full Multigrid Cycles is the start of the algorithm. By Full Multigrid Cycle we start on the coarsest grid solving the equation excactly.

Multigrid for Nonlinear Problems (Brand's Full Approximation Storage (FAS))

Multigrid can be applied directly to nonlinear problems.

To do this we need a non linear relaxation procedure to smooth errors for approximating corrections on coarser grids.

Let's denote a nonlinear elliptic as

\begin{eqnarray} \mathcal L(u) = f\end{eqnarray}

and in a discetized form on a regular grid with mesh size h as

\begin{eqnarray} \mathcal L_{h}(u_{h}) = f_{h}\end{eqnarray}

Suppose we have a nonlinear smoother and the initial solution is already sufficiently smooth

We seek a smooth correction

\begin{eqnarray} v_{h}\end{eqnarray}

to solve

\begin{eqnarray} \mathcal L_{h}(\tilde u_{h}+v_{h}) = f_{h}\end{eqnarray}

To find it note that

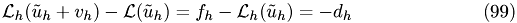
\begin{eqnarray} \mathcal L_{h}(\tilde u_{h}+v_{h}) -\mathcal L(\tilde u_{h}) = f_{h} -\mathcal L_{h}(\tilde u_{h})= -d_{h}\end{eqnarray}

after smoothing steps the defect equation is put onto the coarse grid

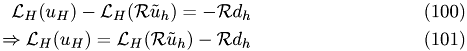
\begin{eqnarray} \mathcal L_{H}(u_{H}) - \mathcal L_{H}(\mathcal R\tilde u_{h}) = -\mathcal Rd_{h} \\\Rightarrow \mathcal L_{H}(u_{H}) = \mathcal L_{H}(\mathcal R\tilde u_{h}) -\mathcal Rd_{h}\end{eqnarray}

The coarse grid correction is given by the difference of coarse and fine grid solution. (Not by solving an equation)

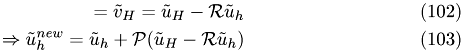
\begin{eqnarray}= \tilde v_{H}= \tilde u_{H}- \mathcal R\tilde u_{h} \\\Rightarrow \tilde u_{h}^{new} = \tilde u_{h} + \mathcal P(\tilde u_{H}- \mathcal R\tilde u_{h})\end{eqnarray}

Termination Criterion for Nonlinear MG

The local truncation error is defined as

\begin{eqnarray} \tau :=\mathcal L_{h}(u)-f_{h}\end{eqnarray}

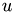where $u$ is the exact solution of the original equation

if we rewrite the equation as follows

\begin{eqnarray}= \Rightarrow \mathcal L_{h}(u) = \tau + f_{h}\end{eqnarray}

we can see that 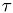$\tau$ can be regarded as the correction of 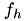$ f_{h}$ so that the solution of the fine-grid equation will be the exact solution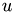 $u$

Since the computation of the truncation error is problematic we consider the relative local truncation error

The relative local truncation error can be seen as the correction to 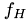$ f_{H} $ that makes the solution of the coarse-grid equation equal to fine-grid solution

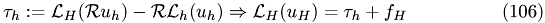
\begin{eqnarray} \tau_{h} :=\mathcal L_{H}(\mathcal Ru_{h})-\mathcal R\mathcal L_{h}(u_{h})\Rightarrow \mathcal L_{H}(u_{H}) = \tau_{h} +f_{H}\end{eqnarray}

Exact relative local truncation errors can not be computed because there are no exact solutions for discretized problems.

A sufficiently accurate estimate of the approximate relative local truncation error can be obtained from using the available approximate solutions

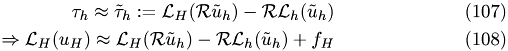
\begin{eqnarray} \tau_{h} \approx \tilde\tau_{h} := \mathcal L_{H}(\mathcal R\tilde u_{h}) - \mathcal R\mathcal L_{h}(\tilde u_{h}) \\\Rightarrow \mathcal L_{H}(u_{H}) \approx \mathcal L_{H}(\mathcal R\tilde u_{h})-\mathcal R\mathcal L_{h}(\tilde u_{h}) + f_{H}\end{eqnarray}

\begin{eqnarray}=\mathcal L_{H}(\mathcal R\tilde u_{h})-\mathcal Rd_{h}\end{eqnarray}

what is just the coarse-grid equation.

Defining Termination Criterion

stop if:

\begin{eqnarray} \left \| d_{h} \right \| \leq \epsilon\end{eqnarray}

The tolerance should not be smaller than the truncation error

Consider the following Taylor-expansions

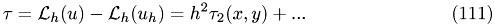
\begin{eqnarray}\tau = \mathcal L_{h}(u)-\mathcal L_{h}(u_{h}) = h^2\tau_{2}(x,y)+...\end{eqnarray}

\begin{eqnarray}u_{h} = u + h^2u_{2}(x,y)+...\end{eqnarray}

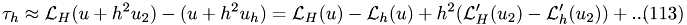
\begin{eqnarray} \tau_{h} \approx \mathcal L_{H}(u+h^2u_{2})-\mathcal(u+h^2u_{h})= \mathcal L_{H}(u) -\mathcal L_{h}(u)+h^2(\mathcal L'_{H}(u_{2}) -\mathcal L'_{h}(u_{2}))+...\end{eqnarray}

\begin{eqnarray} = (H^2-h^2)\tau_{2} + \mathcal O(h^4)\end{eqnarray}

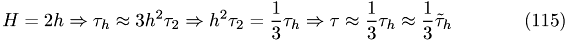
\begin{eqnarray} H = 2h \Rightarrow \tau_{h}\approx 3h^2\tau_{2} \Rightarrow h^2\tau_{2} = \frac{1}{3}\tau_{h}\Rightarrow\tau\approx\frac{1}{3}\tau_{h}\approx\frac{1}{3}\tilde\tau_{h} \end{eqnarray}

The iteration stops when residual and truncation error are of the equal order of magnitude

\begin{eqnarray} \Rightarrow \epsilon :=\frac{1}{3}\left \| \tilde\tau_{h} \right \| \end{eqnarray}

Nonlinear Relaxation Scheme

Using nonlinear Gauss_Seidel requires that nonlinearities are discretized by function values at neighboring points like for derivatives

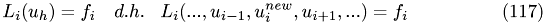
\begin{eqnarray} L_{i}(u_{h}) = f_{i}\;\;\,\;d.h.\;\;\;L_{i}(...,u_{i-1},u^{new}_{i}, u_{i+1},...) = f_i \end{eqnarray}

Do one Newton step

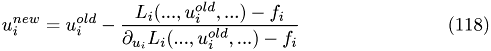
\begin{eqnarray} u^{new}_i = u^{old}_i - \frac{L_i(...,u^{old}_i,...) -f_i}{\partial_{u_{i}} L_i(...,u^{old}_i,...) -f_i} \end{eqnarray}

For example apply the scheme to the Poisson-Boltzman problem in case that only one species of ions is present
(i.e. only constant ions)

\begin{eqnarray} \mathcal L(u) = - \nabla^2u+e^{-\kappa u} -\varrho \end{eqnarray}

Discretized:

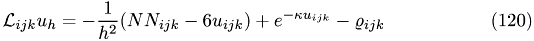
\begin{eqnarray} \mathcal L_{ijk}u_h = -\frac{1}{h^2}(NN_{ijk}-6u_{ijk})+e^{-\kappa u_{ijk}}-\varrho_{ijk} \end{eqnarray}

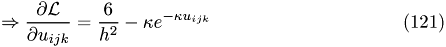
\begin{eqnarray} \Rightarrow \frac{\partial\mathcal L}{\partial u_{ijk}} = \frac{6}{h^2}-\kappa e^{-\kappa u_{ijk}} \end{eqnarray}

Thus, the update ruile is given by

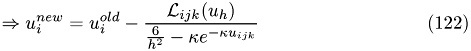
\begin{eqnarray} \Rightarrow u^{new}_i = u^{old}_i - \frac{\mathcal L_{ijk}(u_h)}{\frac{6}{h^2}-\kappa e^{-\kappa u_{ijk}}} \end{eqnarray}

Adaption of PB_Model to CUDA

Put molecule data into constant memory

permittivity function = superposition of Gaussians (sum over monomers omitted)

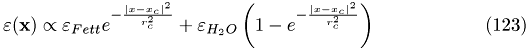
\begin{eqnarray} \varepsilon(\bold x) \propto \varepsilon_{Fett} e^{-\frac{\left |x-x_c \right |^2}{r^2_c}}+\varepsilon_{H_{2}O}\left (1-e^{-\frac{\left |x-x_c \right |^2}{r^2_c}} \right) \end{eqnarray}

permittivity & intramolecular charge distribution as device_functions

intramolecular charge density = sum of sharply peaked Gaussians

Implementation Issues

Literature

The commented program

 #ifndef CUDA_KERNEL_STEP_12_CU_H
 #define CUDA_KERNEL_STEP_12_CU_H
 #define TILE_SIZE 6
 #define MESH_DIM 3

Our goal is to allocate a solution vector as large as possible in CPU memory. MG methods require roughly twice as much memory as is needed for storing the unknows from the finest grid. 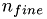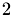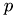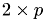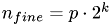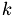Thus, in order to determine the number of grid points at the coarsest mesh we have to start from the number of double values fitting into half of the GPU memory, take its cubic root in order to determine the dimensions of the finest grid $n_{fine}$ Then, we repeatedly divide this number by $2$ until a factor $p$ remains, such that $ 2\times p$ and $ n_{fine} = p\cdot 2^{k} $ where $k$ is the number of divisionswe made, that is 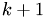$k+1$ is the number of levels in our grid hierarchy
A further constraint is given by the fact, that we want the coarse grid solution to fit completely into the shared memory of a single multiprocessor. As coarse grid solver we take a conjugate gradient method which requires an additional auxiliary array in shared memory which is of the same size as the coarse grid solution. Therefore, on the Fermi architecture the number of points per dim of the coarse grid is limited to 14.

As soon as malloc() is available for shared memory the following will be obsolete.

3**3

 #if MESH_DIM==3
 #define N_POINTS_PHI  27

4**3

 #elif MESH_DIM==4
 #define N_POINTS_PHI  64

5**3

 #elif MESH_DIM==5
 #define N_POINTS_PHI  125

6**3

 #elif MESH_DIM==6
 #define N_POINTS_PHI  216

7**3

 #elif MESH_DIM==7
 #define N_POINTS_PHI  343

8**3

 #elif MESH_DIM==8
 #define N_POINTS_PHI  512

9**3

 #elif MESH_DIM==9
 #define N_POINTS_PHI  729

10**3 //

 #elif MESH_DIM==10
 #define N_POINTS_PHI 1000

11**3

 #elif MESH_DIM==11
 #define N_POINTS_PHI 1331

12**3

 #elif MESH_DIM==12
 #define N_POINTS_PHI 1728

13**3

 #elif MESH_DIM==13
 #define N_POINTS_PHI 2197

14**3

 #elif MESH_DIM==14
 #define N_POINTS_PHI 2744
 #endif
 
 #define N_COARSE_GRID_THREADS 256
 
 
 static const bool print_sols        = false;
 static const int coarse_cg_max_iter = 100;
 static const double cg_tol          = 1e-12;
 
 struct Selectors {
 
     enum TransferTestfunction { one,
                                 x, y, z,
                                 xy, xz, yz,
                                 xyz,
                                 xx, yy, zz,
                                 xxyy, xxyz, yyzz,
                                 xyyz, xyzz, xyzzz };
 
 };

Declarations of Kernel Wrapper Functions

 void coarse_grid_CG_solve_unit_test(float* phi, int n_coarse_points_per_dim,
                                     float tolerance,
                                     int max_iter,
                                     float* residual);
 
 void coarse_grid_CG_solve(float* phi,
                           int n_coarse_points_per_dim,
                           float tolerance,
                           float R,
                           float h,
                           int max_iter,
                           float * residual);
 
 void gauss_seidel(float* phi,
                   int n_intervals_per_dim,
                   float R,
                   float h);
 
 void grid_transfer(float* phi,
                    float* test,
                    int n_intervals_per_dim,
                    bool prolongation);
 
 void MG_reference_solution(float* e_h,
                            float* u_h,
                            int n_intervals_per_dim,
                            float h,
                            float sigma,
                            bool reference_or_error);
 
 
 #ifndef USE_SINGLE_PRECISION
 
 void coarse_grid_CG_solve_unit_test(double* phi, int n_coarse_points_per_dim,
                                     double tolerance,
                                     int max_iter,
                                     double* residual);
 
 void coarse_grid_CG_solve(double* phi, int n_coarse_points_per_dim,
                           double tolerance, double R, double h,
                           int max_iter,
                           double * residual);
 
 void gauss_seidel(double* phi,
                   int n_intervals_per_dim,
                   double R,
                   double h);
 
 void gauss_seidel_unit_test(double* phi,
                   int n_intervals_per_dim,
                   double R,
                   double h);
 
 void grid_transfer(double* phi,
                    double * test,
                    int n_intervals_per_dim,
                    bool prolongation);
 
 void prolongation_unit_test( double * u_H, double * u_h, double* e_H,
                              int n_intervals_per_dim, double h, int current_level,
                              Selectors::TransferTestfunction ftest);
 
 void restriction_unit_test( double * u_H, double * u_h, double* e_H,
                             int n_intervals_per_dim, double h, int current_level,
                             Selectors::TransferTestfunction ftest);
 
 
 void MG_reference_solution(double* e_h, double* u_h,
                            int n_intervals_per_dim,
                            double h,
                            double sigma,
                            bool reference_or_error);
 #endif
 
 #endif // CUDA_KERNEL_STEP_12_CU_H

Header-Datei der CUDA utility-Bibliothek.

 #include <cutil_inline.h>
 #include <cuda_kernel_wrapper_step-12.cu.h>
 
 #define RED_BLACK_DEBUG
 #undef  RED_BLACK_DEBUG
 
 #define RHS_DEBUG
 #undef  RHS_DEBUG

Device Functions and Functors

Class: Constant

 template <typename T>
 class Constant{
 
 public:
     typedef  T NumberType;
     __device__ Constant(){}
 
     __forceinline__ __device__
     const T operator ()(const T x, const T y ,const T z) const
     {
         return 1;
     }
 
 };

Class: X

 template <typename T>
 class X{
 
 public:
     typedef  T NumberType;
     __device__ X(){}
 
     __forceinline__ __device__
     const T operator ()(const T x, const T y ,const T z) const
     {
 
         return x;
     }
 };

Class: Y

 template <typename T>
 class Y{
 
 public:
     typedef  T NumberType;
     __device__ Y(){}
 
     __forceinline__ __device__
     const T operator ()(const T x, const T y ,const T z) const
     {
 
         return y;
     }
 
 };

Class: Z

 template <typename T>
 class Z{
 
 public:
      typedef  T NumberType;
 
     __device__ Z(){}
 
     __forceinline__ __device__
     const T operator ()(const T x, const T y ,const T z) const
     {
 
         return z;
     }
 };

Class: F

 template<typename FX, typename FY, typename FZ>
 class F{
 
 public:
 
     typedef typename FX::NumberType NumberType;
     typedef typename FX::NumberType T;
 
     __device__ F() : fx(), fy(), fz() {}
 
     __forceinline__ __device__
     const T operator() (const T x, const T y, const T z) const
     {
         return fx(x,y,z) * fy(x,y,z) * fz(x,y,z);
     }
 private:
     FX fx;
     FY fy;
     FZ fz;
 };

Class: MG_Unit_Test_problem

class for testing the Multigrid solver

 template<typename T>
 class MG_Unit_Test_Curved_Ridges{
 
 public:
     typedef LaplaceOp<T> DiffOp;
 
     MG_Unit_Test_Curved_Ridges(){}

sect5{Class: RHS}

     class RHS{
     public:
         RHS(int n_points_per_dim,T h)
             :
             _n_points_per_dim(n_points_per_dim),
             _h(h)
         {}
 
         __forceinline__ __device__
         T operator () (const dim3 &grid_pos) const
         {
             Stencil stencil(_n_points_per_dim);
 
             stencil (grid_pos);
 
             int n_intervals_per_dim = _n_points_per_dim-1;
 
             bool boundary = (grid_pos.x == 0) || (grid_pos.x == n_intervals_per_dim)
                          || (grid_pos.y == 0) || (grid_pos.y == n_intervals_per_dim)
                          || (grid_pos.z == 0) || (grid_pos.z == n_intervals_per_dim);
 
             if (boundary)
                 return ref_sol(grid_pos);
             else
             return
                 / *partial with respect to x * /
                 5 * M_PI *(
                          10 * M_PI*(grid_pos.x*_h)
                          *(cos(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                          *(cos(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                          *(exp(2*sin(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                            - 8 * grid_pos.z * grid_pos.z )
                          +(exp(2*sin(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                            - 8 * grid_pos.z * grid_pos.z )
                          *(cos(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                          + 5 *M_PI*(grid_pos.*_h + 1)
                          *
                          (sin(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                         )
                 / *partial with respect to y * /
                 +
                 10 * M_PI*(grid_pos.*_h + 1)
                 *((10*M_PI*grid_pos.y*_h * grid_pos.y * _h)
                 *(cos(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                 *(cos(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h)))))
                 *(exp(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                 - 4 * grid_pos.z * grid_pos.z
                 +(exp(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                 - 4 * grid_pos.z * grid_pos.z
                 *(cos(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                 -(5*M_PI*grid_pos.y*_h * 2*grid_pos.y * _h)
                 *(sin(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
 
                 / *Partial wit respect to z* /
                 +
                 8 * (grid_pos.x*_h + 1)
                 *(8*(grid_pos.z*grid_pos.z) - 1)
                 *(exp(sin(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h) ))
                 - 4 * grid_pos.z*_h *grid_pos.z *_h ));
 
 
 
         }
         __forceinline__ __device__
                 T
                 ref_sol(dim3 grid_pos) const
         {
             return (1 + grid_pos.x*_h)* exp(-4.0 * (grid_pos.z*_h * grid_pos.z*_h) + sin(5*M_PI*(grid_pos.x*_h + grid_pos.y*_h * grid_pos.y*_h)));
         }
     private:
         int _n_points_per_dim;
         T _h;
 
     };
 };
 
 
 template<typename T>
 class MG_Unit_Test_Gauss{
 
 public:
     typedef LaplaceOp<T> DiffOp;
 
 
     MG_Unit_Test_Gauss(){}

sect5{Class: RHS}

     class RHS{
     public:
         RHS(int n_points_per_dim,T h, T sigma)
             :
             _n_points_per_dim(n_points_per_dim),
             _h(h),
             _sigma2(sigma*sigma)
 
         {}
 
         __forceinline__ __device__
         T operator () (const dim3 &grid_pos) const
         {
             Stencil stencil(_n_points_per_dim);
 
             stencil (grid_pos);
 
             int n_intervals_per_dim = _n_points_per_dim-1;
 
             bool boundary = (grid_pos.x == 0) || (grid_pos.x == n_intervals_per_dim)
                          || (grid_pos.y == 0) || (grid_pos.y == n_intervals_per_dim)
                          || (grid_pos.z == 0) || (grid_pos.z == n_intervals_per_dim);
 
 
             if (boundary)
             {
                  return ref_sol(grid_pos);
             }
 
             else
             {
                 T x2 = grid_pos.x*_h * grid_pos.x*_h;
                 T y2 = grid_pos.y*_h * grid_pos.y*_h;
                 T z2 = grid_pos.z*_h * grid_pos.z*_h;

T s1 = 1/_sigma2; T s2 = 2/_sigma2; T s4 = s2 * s2;

                 T f = exp(-16 *(x2 + y2 + z2));
 
 
 
                 return (-32 + 1024*x2) * f
                       +(-32 + 1024*y2) * f
                       +(-32 + 1024*z2) * f;
             }
 
 
 
 
         }
         __forceinline__ __device__
                 T
                 ref_sol(const dim3 grid_pos) const
         {
             return    exp(-16 *((grid_pos.x*_h * grid_pos.x*_h )
                              + (grid_pos.y*_h * grid_pos.y*_h )
                              + (grid_pos.z*_h * grid_pos.z*_h )
                              ));
 
 
         }
 
 
     private:
         int _n_points_per_dim;
         T _h;
         T _sigma2;
 
 
     };
 
 };

Function: red_black_ordering

used to find out whether an element belongs to red or black subset.

 __device__ int __red_black_ordering(int i, int j, int k){
 
     if( (i%2 == 0 && j%2==0 && k%2==0) || (i%2 == 1 && j%2==1 && k%2==0) ||
         (i%2 == 0 && j%2==1 && k%2==1) || (i%2 == 1 && j%2==0 && k%2==1))
         return 0;
 
     return 1;
 
 }

Function: is_bound

 __device__ bool _is_bound (dim3 grid_pos, int dim){
 
     if(grid_pos.x == 0 || grid_pos.x == dim-1 ||
        grid_pos.y == 0 || grid_pos.y == dim-1 ||
        grid_pos.z == 0 || grid_pos.z == dim-1)
     {
         return true;
     }
 
     return false;
 
 }

Function: sweep_test

The function tests the sweep functionality

 template<typename T, typename DiffOp, typename RHS>
 __forceinline__ __device__
 void
 __sweep_test(T* phi, int i, int j, int n_intervals_per_dim, bool d,
         bool boundary_cond, DiffOp &laplace, const RHS &f){
 
     int color;
     int index;
 
     int dim_1 = n_intervals_per_dim + 1;
 
     if(d){
         index = 0;
     }else{
         index = 1;
     }
     dim3 grid_pos(i,j,0);
 
     Stencil stencil(dim_1);
 
     for(int k=1; k<dim_1-1; k++){
 
 
         grid_pos.z = k;
 
         color = __red_black_ordering(i,j,k);
 
         if(color == index)
         {
 
             if(!boundary_cond){
 
                 stencil(grid_pos);
                 phi[stencil.site] = stencil.site;
 
             }
          }
        __syncthreads();
     }
 }

Function: sweep

The function updates the values of the reference solutions
in red-black order. The function called by guass_seidel kernel.

 template<typename T, typename DiffOp, typename RHS>
 __forceinline__ __device__
 void
 __sweep(T* phi, int i, int j, int n_intervals_per_dim, bool d,
         bool boundary_cond, DiffOp &laplace, const RHS &f){
 
     int color;
     int index;
 
     int dim_1 = n_intervals_per_dim + 1;
 
     if(d){
         index = 0;
     }else{
         index = 1;
     }
     dim3 grid_pos(i,j,0);
 
     Stencil stencil(dim_1);
 
     for(int k=1; k<dim_1-1; k++){
 
 
         grid_pos.z = k;
 
         color = __red_black_ordering(i,j,k);
 
         if(color == index)
         {
 
             if(!boundary_cond){
 
                 stencil(grid_pos);
 
                 phi[stencil.site] -= (laplace(stencil, phi)-f(grid_pos))
                                      /
                                     laplace.grad_u(stencil, phi);
 
             }
          }
 
         __syncthreads();
     }
 }

Device Function: __in_range

Parameters:
i : index to check, whether 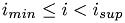$i_{min} \le i < i_{sup}$.
i_min : lower bound of interval
i_sup : upper bound of interval
 __device__ bool in_range(int i, int i_min, int i_sup)
 {
     return ((i >= i_min) && (i < i_sup));
 }

Device Function: boundary_cond

 __device__ bool __boundary_cond(int n_intervals_per_dim, int Halo_width, int i, int j){
 
     return !(in_range(i, Halo_width, n_intervals_per_dim + 1 - Halo_width)
          &&
             in_range(j, Halo_width, n_intervals_per_dim + 1 - Halo_width)
            );
 }

Kernel: __gauss_seidel

The kernel delegates its work to the __sweep() function so that one does not have to implement the same functionality for the red and the black subgrid twice.

 template<typename T, typename DiffOp, typename RHS>
 __global__
 void __gauss_seidel(T* phi, int n_intervals_per_dim,
                     DiffOp laplace,
                     const RHS f)
 {
     int j = blockIdx.x * blockDim.x + threadIdx.x;
     int i = blockIdx.y * blockDim.y + threadIdx.y;
     bool cond;
     int Halo_width = 1;
 
     bool RED   = true;
     bool BLACK = false;
 
     if(i > (n_intervals_per_dim) && (j > n_intervals_per_dim) ) return;
 
     cond = __boundary_cond(n_intervals_per_dim, Halo_width, i , j);
 
     __sweep(phi, i, j, n_intervals_per_dim, RED, cond, laplace, f);
     __syncthreads();
 
     __sweep(phi, i, j, n_intervals_per_dim, BLACK, cond, laplace, f);
     __syncthreads();
 }

Kernel: __grid_transfer

The function delegates its work to the appropriate transfer operator.

 template<typename T, typename TransferOp>
 __global__ void __grid_transfer(T* phi_H, T* phi_h, int n_intervals_per_dim,
                                 TransferOp transfer,bool prolongation)
 {
 
     int i = blockIdx.x * blockDim.x + threadIdx.x;
     int j = blockIdx.y * blockDim.y + threadIdx.y;
 
     int in_dim_1 = n_intervals_per_dim + 1;
 
     if (i >= in_dim_1) return;
     if (j >= in_dim_1) return;
 
     dim3 grid_pos(i,j,0);
 
     for(int k=0; k<in_dim_1; k++){
 
         grid_pos.z = k;
         / *printf("%d", site);* /
         if(prolongation)
         {
             transfer.prolongate(grid_pos, in_dim_1, phi_H, phi_h);
         }
         else
         {
             transfer.restriction(grid_pos, in_dim_1, phi_H, phi_h);
         }
 
         __syncthreads();
     }
 }
 
 
 #include "cuda_coarse_grid_cg.cu.c"

Wrapper Function: _gauss_seidel_unit_test

Used for testing purposes of the guass-seidel solver.
The variable n_threads_per_block_dim corresponds to CUDA compute capability.
On Fermi architecture it is possible to start 32 threads per block dimension.

 template<typename T>
 void
 _gauss_seidel_unit_test(T* phi, int n_intervals_per_dim, T R, T h)
 {
 #if __CUDA_ARCH__ < 200
     int n_threads_per_block_dim = 16;
 #else
     int n_threads_per_block_dim = 32;
 #endif
     int blocks_per_dim = ((n_intervals_per_dim + 1)
                        +
                        n_threads_per_block_dim - 1)/n_threads_per_block_dim;
 
     int n_points_per_dim = (n_intervals_per_dim + 1);
     / *printf(" n block per dim %d \n",blocks_per_dim); * /
     dim3 grid(blocks_per_dim, blocks_per_dim);
     dim3 blocks(n_threads_per_block_dim,n_threads_per_block_dim);
     __gauss_seidel<<<grid,blocks>>>(phi,
                                     n_intervals_per_dim,
                                     typename MG_Unit_Test_Gauss<T>::DiffOp(),
                                     typename MG_Unit_Test_Gauss<T>::RHS(n_intervals_per_dim + 1,h, R)
     / *
                                     typename CGUnitTestProblem<T>::DiffOp(),
                                     typename CGUnitTestProblem<T>::RHS(n_points_per_dim)* /
                                     );
     cudaThreadSynchronize();
 }

Wrapper Function: _gauss_seidel

 template<typename T>
 void
 _gauss_seidel(T* phi, int n_intervals_per_dim, T h, T sigma)
 {
 #if __CUDA_ARCH__ < 200
     int n_threads_per_block_dim = 16;
 #else
     int n_threads_per_block_dim = 32;
 #endif
     int blocks_per_dim = ((n_intervals_per_dim + 1)
                        +
                        n_threads_per_block_dim - 1)/n_threads_per_block_dim;
 
     / *printf(" n block per dim %d \n",blocks_per_dim);* /
     dim3 grid(blocks_per_dim, blocks_per_dim);
     dim3 blocks(n_threads_per_block_dim,n_threads_per_block_dim);
     __gauss_seidel<<<grid,blocks>>>(phi, n_intervals_per_dim,
                           typename MG_Unit_Test_Gauss<T>::DiffOp(),
                           typename MG_Unit_Test_Gauss<T>::RHS(n_intervals_per_dim + 1, h, sigma));
     cudaThreadSynchronize();
 }

Wrapper Function: _grid_transfer

 template<typename T>
 void
 _grid_transfer(T* phi_H, T* phi_h, int n_intervals_per_dim, bool prolongation)
 {
 #if __CUDA_ARCH__ < 200
     int n_threads_per_block_dim = 16;
 #else
     int n_threads_per_block_dim = 32;
 #endif
     int blocks_per_dim = ((n_intervals_per_dim+1)
                        +
                        n_threads_per_block_dim)/n_threads_per_block_dim;
 
     
     dim3 grid(blocks_per_dim, blocks_per_dim);
     
     dim3 blocks(n_threads_per_block_dim, n_threads_per_block_dim);
 
     __grid_transfer<<<grid,blocks>>>(phi_H, phi_h, n_intervals_per_dim,
                           InterGridOperator<T>(),prolongation);
 
     cudaThreadSynchronize();
 }

Template specializations

 void gauss_seidel(float* phi, int n_intervals_per_dim, float h, float sigma)
 {
     _gauss_seidel(phi, n_intervals_per_dim, h, sigma);
 }
 
 void gauss_seidel_unit_test(float* phi, int n_intervals_per_dim, float R, float h)
 {
     _gauss_seidel_unit_test(phi, n_intervals_per_dim, R, h);
 }
 
 void grid_transfer(float* phi_H, float * phi_h, int n_intervals_per_dim,
                     bool prolongation)
 {
     _grid_transfer(phi_H, phi_h,  n_intervals_per_dim, prolongation);
 }
 
 
 
 #ifndef USE_SINGLE_PRECISION
 void gauss_seidel(double* phi, int n_intervals_per_dim, double h, double sigma)
 {
     _gauss_seidel(phi, n_intervals_per_dim, h, sigma);
 }
 
 void gauss_seidel_unit_test(double* phi, int n_intervals_per_dim, double R, double h)
 {
     _gauss_seidel_unit_test(phi, n_intervals_per_dim, R, h);
 }
 
 void grid_transfer(double* phi_H, double * phi_h,
                    int n_intervals_per_dim, bool prolongation)
 {
     _grid_transfer(phi_H, phi_h,  n_intervals_per_dim, prolongation);
 }
 #endif

Kernel Function: prolongation_unit_test

The function tests the prolongation operator. The output of the transfer is compared with the reference solution computed analytically.

 template <typename T, typename F>
 __global__
 void
 __prolongation_unit_test( T * u_H, T * u_h, T* e_H, int n_intervals_per_dim, T h, int current_level)
 {
 
     int i = blockIdx.x * blockDim.x + threadIdx.x;
     int j = blockIdx.y * blockDim.y + threadIdx.y;
 
     int in_dim_1 = n_intervals_per_dim + 1;
 
     T tmp, tmp_e;
     dim3 grid_pos_h(i,j,0);
     dim3 grid_pos_H(i/2, j/2,0);
     T H = 2*h;
 
     if (i >= in_dim_1) return;
     if (j >= in_dim_1) return;
 
     Stencil s_h(in_dim_1);
     Stencil s_H(n_intervals_per_dim/2 + 1);
     const F f;
     InterGridOperator<T> transfer;
 
 
     for(int k=0; k<in_dim_1; k+=2){
 
         if( (grid_pos_h.x%2 == 0) && (grid_pos_h.y%2 == 0) )
         {
             grid_pos_H.z = k/2;
             s_H(grid_pos_H);
 
             tmp = f(H*grid_pos_H.x, H*grid_pos_H.y, H*grid_pos_H.z);
 
             if (current_level == 0)
                 u_H[s_H.site] = tmp;
 
             tmp_e = u_H[s_H.site] - tmp;
             / *e_H[s_H.site] =  u_H[s_H.site];* /
             e_H[s_H.site] = tmp_e * tmp_e;
             / * u_H[s_H.site] = tmp;* /
         }        
     }
 __syncthreads();
 
 
     for(int k=0; k<in_dim_1; k++){
 
         grid_pos_h.z = k;
 
         transfer.prolongate(grid_pos_h, in_dim_1, u_H, u_h);
 
         if (is_boundary_point(grid_pos_h, in_dim_1))
         {
             s_h(grid_pos_h);
             tmp = f(h*grid_pos_h.x, h*grid_pos_h.y, h*grid_pos_h.z);
             u_h[s_h.site] = tmp;
         }
 
         __syncthreads();
     }
 
 }

Wrapper Function: _prolongation_unit_test

The wrapper function passes the test function(s) chosen in the parameter file to the kernel.

 template<typename T>
 void
 _prolongation_unit_test( T * u_H, T * u_h, T* e_H,
                          int n_intervals_per_dim, T h, int current_level,
                          Selectors::TransferTestfunction ftest)
 {
 
 #if __CUDA_ARCH__ < 200
     int n_threads_per_block_dim = 16;
 #else
     int n_threads_per_block_dim = 16;
 #endif
     int blocks_per_dim = ((n_intervals_per_dim)
                        +
                        n_threads_per_block_dim)/n_threads_per_block_dim;
 
     dim3 grid(blocks_per_dim, blocks_per_dim);
 
     dim3 blocks(n_threads_per_block_dim, n_threads_per_block_dim);
 
 
     typedef Constant<T> one;
 
     typedef F< X<T>,        Constant<T>, Constant<T> > x;
     typedef F< Constant<T>, Y<T>,        Constant<T> > y;
     typedef F< Constant<T>, Constant<T>, Z<T>        > z;
 
     typedef F< x, y, one > xy;
     typedef F< x, one, z > xz;
     typedef F< one, y, z > yz;
     typedef F< x, y, z > xyz;
 
     typedef F< x, x, one > xx;
     typedef F< y, y, one > yy;
     typedef F< one, z, z > zz;
 
     typedef F< z, z, z > zzz;
 
     typedef F< xx, yy, one > xxyy;
     typedef F< xx, yy, z > xxyz;
     typedef F< one,Y<T>, Y<T> > yyzz;
     typedef F< x, yy, z> xyyz;
     typedef F< x,y , zz> xyzz;
 
     typedef F< x, y, zzz > xyzzz;

The kernel function testing grid transfer operator runs appropriate unit_test depending on type of function that should be tested.

     switch (ftest) {
     case Selectors::one:
          __prolongation_unit_test<T,one><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::x:
          __prolongation_unit_test<T,x><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::y:
          __prolongation_unit_test<T,y><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::z:
          __prolongation_unit_test<T,z><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xy:
          __prolongation_unit_test<T,xy><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xz:
          __prolongation_unit_test<T,xz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::yz:
          __prolongation_unit_test<T,yz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyz:
          __prolongation_unit_test<T,xyz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xx:
          __prolongation_unit_test<T,xx><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::yy:
          __prolongation_unit_test<T,yy><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::zz:
          __prolongation_unit_test<T,zz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xxyy:
          __prolongation_unit_test<T,xxyy><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xxyz:
          __prolongation_unit_test<T,xxyz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::yyzz:
          __prolongation_unit_test<T,yyzz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyyz:
          __prolongation_unit_test<T,xyyz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyzz:
          __prolongation_unit_test<T,xyzz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyzzz:
          __prolongation_unit_test<T,xyzzz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
 
     default:
          break;
     }
 
     cudaThreadSynchronize();
 }

template specialization

 void prolongation_unit_test( double * u_H, double * u_h, double* e_H,
                              int n_intervals_per_dim, double h, int current_level, Selectors::TransferTestfunction ftest)
 {
     _prolongation_unit_test(u_H, u_h, e_H, n_intervals_per_dim, h, current_level, ftest);
 }

Kernel Function: restriction_unit_test

The function tests the restriction operator. The output of the transfer is compared with the reference solution computed analytically.

 template <typename T, typename F>
 __global__
 void
 __restriction_unit_test( T * u_H, T * u_h, T* e_H, int n_intervals_per_dim, T h, int current_level)
 {
 
     int i = blockIdx.x * blockDim.x + threadIdx.x;
     int j = blockIdx.y * blockDim.y + threadIdx.y;
 
     int in_dim_1 = n_intervals_per_dim + 1;
 
     T tmp, tmp_e;
     dim3 grid_pos_h(i,j,0);
     dim3 grid_pos_H(i/2, j/2,0);
     T H = 2*h;
 
     if (i >= in_dim_1) return;
     if (j >= in_dim_1) return;
 
     Stencil s_h(in_dim_1);
     Stencil s_H((n_intervals_per_dim/2) + 1);
     const F f;
     InterGridOperator<T> transfer;
 
 
 
     if (current_level == 0){
 
         for(int k=0; k<in_dim_1; k++){
 
             s_h(grid_pos_h);
             tmp = f(h*grid_pos_h.x, h*grid_pos_h.y, h*grid_pos_h.z);
             u_h[s_h.site] = tmp;
 
         }
 
     }
 
 
 
     for(int k=0; k<in_dim_1; k++){
 
         grid_pos_h.z = k;
 
         transfer.restriction(grid_pos_h, in_dim_1, u_H, u_h);
 
         if (is_boundary_point(grid_pos_h, in_dim_1))
         {
             s_h(grid_pos_h);
             tmp = f(h*grid_pos_h.x, h*grid_pos_h.y, h*grid_pos_h.z);
             u_h[s_h.site] = tmp;
         }
 
         __syncthreads();
     }
 
     for(int k=0; k<in_dim_1; k+=2){
 
         if( (grid_pos_h.x%2 == 0) && (grid_pos_h.y%2 == 0) )
         {
             grid_pos_H.z = k/2;
             s_H(grid_pos_H);
 
             tmp = f(H*grid_pos_H.x, H*grid_pos_H.y, H*grid_pos_H.z);
 
             tmp_e = u_H[s_H.site] - tmp;
             / *e_H[s_H.site] =  u_H[s_H.site];* /
             e_H[s_H.site] = tmp_e * tmp_e;
            / * u_H[s_H.site] = tmp;* /
         }
     }
 
 }

Wrapper Function: _restriction_unit_test

The wrapper function passes the test function(s) chosen in the parameter file to the kernel.

 template<typename T>
 void
 _restriction_unit_test( T * u_H, T * u_h, T* e_H,
                         int n_intervals_per_dim, T h, int current_level,
                         Selectors::TransferTestfunction ftest)
 {
 
 #if __CUDA_ARCH__ < 200
     int n_threads_per_block_dim = 16;
 #else
     int n_threads_per_block_dim = 16;
 #endif
     int blocks_per_dim = ((n_intervals_per_dim)+n_threads_per_block_dim)/n_threads_per_block_dim;
 
     dim3 grid(blocks_per_dim, blocks_per_dim);
 
     dim3 blocks(n_threads_per_block_dim, n_threads_per_block_dim);
 
     typedef Constant<T> one;
 
     typedef F< X<T>,        Constant<T>, Constant<T> > x;
     typedef F< Constant<T>, Y<T>,        Constant<T> > y;
     typedef F< Constant<T>, Constant<T>, Z<T>        > z;
 
     typedef F< x, y, one > xy;
     typedef F< x, one, z > xz;
     typedef F< one, y, z > yz;
     typedef F< x, y, z > xyz;
     typedef F< x, x, one > xx;
     typedef F< y, y, one > yy;
     typedef F< one, z, z > zz;
 
     typedef F< z, z, z > zzz;
 
 
     typedef F< xx, yy, one > xxyy;
     typedef F< xx, yy, z > xxyz;
     typedef F< one,Y<T>, Y<T> > yyzz;
     typedef F< x, yy, z> xyyz;
     typedef F< x,y , zz> xyzz;
 
     typedef F< x, y, zzz > xyzzz;

The kernel function testing grid transfer operator runs appropriate unit_test depending on type of function that should be tested.

     switch (ftest) {
     case Selectors::one:
          __restriction_unit_test<T,one><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::x:
          __restriction_unit_test<T,x><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::y:
          __restriction_unit_test<T,y><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::z:
          __restriction_unit_test<T,z><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xy:
          __restriction_unit_test<T,xy><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xz:
          __restriction_unit_test<T,xz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::yz:
          __restriction_unit_test<T,yz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyz:
          __restriction_unit_test<T,xyz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xx:
          __restriction_unit_test<T,xx><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::yy:
          __restriction_unit_test<T,yy><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::zz:
          __restriction_unit_test<T,zz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xxyy:
          __restriction_unit_test<T,xxyy><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xxyz:
          __restriction_unit_test<T,xxyz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::yyzz:
          __restriction_unit_test<T,yyzz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyyz:
          __restriction_unit_test<T,xyyz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyzz:
          __restriction_unit_test<T,xyzz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyzzz:
          __restriction_unit_test<T,xyzzz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
 
     default:
          break;
     }
 
     cudaThreadSynchronize();
 }

template specialization

 void restriction_unit_test( double * u_H, double * u_h, double* e_H,
                             int n_intervals_per_dim, double h, int current_level,
                             Selectors::TransferTestfunction ftest)
 {
     _restriction_unit_test(u_H, u_h, e_H,
                            n_intervals_per_dim, h,
                            current_level, ftest);
 }

Kernel: __MG_reference_solution

The kernel delegates its work to the __sweep_test() function so that one does not have to implement the same functionality for the red and the black subgrid twice.

 template<typename T, typename DiffOp, typename RHS>
 __global__
 void __MG_reference_solution(T* e_h, T* u_h, int n_intervals_per_dim,
                             DiffOp laplace,
                             const RHS f, bool reference_or_error)
 {
     int j = blockIdx.x * blockDim.x + threadIdx.x;
     int i = blockIdx.y * blockDim.y + threadIdx.y;
 
     if (i > n_intervals_per_dim) return;
     if (j > n_intervals_per_dim) return;
 
     int dim_1 = n_intervals_per_dim + 1;
 
     dim3 grid_pos(i,j,0);
 
     Stencil stencil(dim_1);
 
 
     for(int k=0; k<dim_1; k++){
 
         grid_pos.z = k;
 
         stencil(grid_pos);
 
         if( _is_bound (grid_pos,  n_intervals_per_dim))
         {
             u_h[stencil.site] = f.ref_sol(grid_pos);
         }
 
         if(reference_or_error) // reference
         {
             e_h[stencil.site] = f.ref_sol(grid_pos);
         }
         else //or error
         {
             e_h[stencil.site] = f.ref_sol(grid_pos);
             e_h[stencil.site] -= u_h[stencil.site];
         }
 
     }
 }

Wrapper Function: _MG_reference_solution

Used for testing purposes of the Multigid solver.
The variable n_threads_per_block_dim corresponds to CUDA compute capability.
On Fermi architecture it is possible to start 32 threads per block dimension.

 template<typename T>
 void
 _MG_reference_solution(T* e_h, T* u_h, int n_intervals_per_dim, T h, T sigma, bool reference_or_error)
 {
 #if __CUDA_ARCH__ < 200
     int n_threads_per_block_dim = 16;
 #else
     int n_threads_per_block_dim = 32;
 #endif
     int blocks_per_dim = ((n_intervals_per_dim + 1)
                        +
                        n_threads_per_block_dim - 1)/n_threads_per_block_dim;
 
     / *printf(" n block per dim %d \n",blocks_per_dim);* /
     dim3 grid(blocks_per_dim, blocks_per_dim);
     dim3 blocks(n_threads_per_block_dim,n_threads_per_block_dim);
     __MG_reference_solution<<<grid,blocks>>>(e_h,u_h,n_intervals_per_dim,
                                     typename MG_Unit_Test_Gauss<T>::DiffOp(),
                                     typename MG_Unit_Test_Gauss<T>::RHS((n_intervals_per_dim + 1), h, sigma),
                                     reference_or_error);
     cudaThreadSynchronize();
 }
 
 
 
 
 
 
 void MG_reference_solution(float* e_h, float* u_h, int n_intervals_per_dim, float h, float sigma, bool reference_or_error)
 {
     _MG_reference_solution(e_h, u_h, n_intervals_per_dim, h, sigma, reference_or_error);
 }
 
 #ifndef USE_SINGLE_PRECISION
 void MG_reference_solution(double* e_h, double* u_h, int n_intervals_per_dim, double h, double sigma, bool reference_or_error)
 {
     _MG_reference_solution(e_h, u_h, n_intervals_per_dim, h, sigma, reference_or_error);
 }
 #endif
 
 
 
 
 
 #ifndef CUDADriver_STEP_12_H
 #define CUDADriver_STEP_12_H
 
 #include <lac/blas++.h>
 #include <base/parameter_handler.h>
 #include <cuda_kernel_wrapper_step-12.cu.h>

Every program uses a separate namespace, in order to be able to combine different Driver classes or more coplex projects in the future.

 namespace step12 {

Struct: SimParam

The structure is used to create a parameter file. It allows changing parameter at execution time.

     struct SimParam {
 
         static void declare(::ParameterHandler & prm);
         void get(::ParameterHandler & prm);
         void run(std::string prm_filename);
 
         int max_level;
         bool disp_mem_consumption, disp_phi_max_size, disp_error_matrix,
              disp_transfer_dimension_resize_info, disp_transfer_error, disp_data_matrix,
              disp_transfer_time, disp_pointer, disp_current_level;
 
         std::string n_cycle;
 
         QString test_functions;
 
         std::vector<Selectors::TransferTestfunction> tests;
         std::map<QString, Selectors::TransferTestfunction> prm_name2enum,
                                                            transfer_tests;
 
         SimParam(){
             prm_name2enum["one"]=Selectors::one;
             prm_name2enum["x"]=Selectors::x;
             prm_name2enum["y"]=Selectors::y;
             prm_name2enum["z"]=Selectors::z;
             prm_name2enum["xy"]=Selectors::xy;
             prm_name2enum["xz"]=Selectors::xz;
             prm_name2enum["yz"]=Selectors::yz;
             prm_name2enum["xyz"]=Selectors::xyz;
             prm_name2enum["xx"]=Selectors::xx;
             prm_name2enum["yy"]=Selectors::yy;
             prm_name2enum["zz"]=Selectors::zz;
             prm_name2enum["xxyy"]=Selectors::xxyy;
             prm_name2enum["xxyz"]=Selectors::xxyz;
             prm_name2enum["yyzz"]=Selectors::yyzz;
             prm_name2enum["xyyz"]=Selectors::xyyz;
             prm_name2enum["xyzz"]=Selectors::xyzz;
             prm_name2enum["xyzzz"]=Selectors::xyzzz;
 
         }
 
     };

Function: declare

     void
     SimParam::declare(::ParameterHandler &prm)
     {
         prm.enter_subsection("Choose unit test");
 
         prm.declare_entry("Max level", "1",
                           ::Patterns::Integer(),
                           "Maximum level of multigrid cycles.\n"
                           "  # Possible values : 1,2,3...");
         prm.declare_entry("Type of cycle", "v",
                           ::Patterns::Anything(),
                           "Type of Cycle(v,w). "
                           "Multigrid cycles types defined in Wesseling"
                           "  # Possible values: v,w");
 
         prm.declare_entry("Display memory consumption", "false",
                           ::Patterns::Bool(),
                           "Displaying memory consumption of all solutions"
                           "");
 
         prm.declare_entry("Display finest grid size", "false",
                           ::Patterns::Bool(),
                           "Displaying grid size of the maximum level"
                           "");

mg_unit_test.test_coarse_CG_solver();

mg_unit_test.test_gauss_seidel();

mg_unit_test.test_grid_transfer();

         mg_unit_test.test_Multigrid();
 
 
         prm.leave_subsection();
 
         prm.enter_subsection("Grid transfer tests");
 
         prm.declare_entry("Test functions", "one, x, y, z",
                           ::Patterns::Anything(),
                           "Functions for testing the multigrid transfer. "
                           "Transfer is done via multilinear interpolation."
                           "Test functions comprise the set of functions "
                           "that can be transferred exactly (all multilinear"
                           "combinations of one, x,y,z)"
                           "and several which are quadratic or cubic in one component"
                           "in order to reproduce"
                           "interpolation errors."
                           "Possible values : one, x, y, z, xy, xz, yz, xyz, xx, yy, zz, xxyy, xxyz, "
                           "yyzz, xyyz, xyzz, xyzzz");
 
         prm.declare_entry("Max level", "1",
                           ::Patterns::Integer(),
                           "Maximum level of multigrid cycles.\n"
                           "  # Possible values : 1,2,3...");
         prm.declare_entry("Type of cycle", "v",
                           ::Patterns::Anything(),
                           "Type of Cycle(v,w). "
                           "Multigrid cycles types defined in Wesseling"
                           "  # Possible values: v,w");
 
         prm.declare_entry("Display memory consumption", "false",
                           ::Patterns::Bool(),
                           "Displaying memory consumption of all solutions"
                           "");
 
         prm.declare_entry("Display finest grid size", "false",
                           ::Patterns::Bool(),
                           "Displaying grid size of the maximum level"
                           "");
         prm.declare_entry("Display error matrix", "false",
                           ::Patterns::Bool(),
                           "Displaying error matrix of one resizing step"
                           "");
         prm.declare_entry("Display dimension information", "false",
                           ::Patterns::Bool(),
                           "Displaying dimensions of the current reference solution "
                           "matrix "
                           "");
         prm.declare_entry("Display transfer error", "false",
                           ::Patterns::Bool(),
                           "Displaying l2 norm of the error vector of one resizing step."
                           "");
         prm.declare_entry("Display reference solution", "false",
                           ::Patterns::Bool(),
                           "Displaying current reference solution matrix "
                           "containing actual data "
                           "");
         prm.declare_entry("Display transfer time", "false",
                           ::Patterns::Bool(),
                           "Displaying transfer time between two levels"
                           "");
         prm.declare_entry("Display pointers", "false",
                           ::Patterns::Bool(),
                           "Displaying begin of the areas within the whole "
                           "refernce solution vector"
                           "");
         prm.declare_entry("Display current level", "false",
                           ::Patterns::Bool(),
                           "Displaying level of a current multigrid cycle, "
                           "0 at the bottom"
                           "");
 
         prm.leave_subsection();
 
         prm.enter_subsection("Grid transfer tests");
 
         prm.leave_subsection();
     }

Function: get

     void
     SimParam::get(::ParameterHandler &prm)
     {
         prm.enter_subsection("Grid transfer tests");
 
         test_functions = QString(prm.get("Test functions").c_str());
         max_level = prm.get_integer("Max level");
         n_cycle = prm.get("Type of cycle");
         disp_mem_consumption = prm.get_bool("Display memory consumption");
         disp_phi_max_size = prm.get_bool("Display finest grid size");
         disp_error_matrix = prm.get_bool("Display error matrix");
         disp_transfer_dimension_resize_info = prm.get_bool("Display dimension information");
         disp_transfer_error = prm.get_bool("Display transfer error");
 
         disp_data_matrix = prm.get_bool("Display reference solution");
         disp_transfer_time = prm.get_bool("Display transfer time");
         disp_pointer = prm.get_bool("Display pointers");
         disp_current_level = prm.get_bool("Display current level");
 
         prm.leave_subsection();
 
         QStringList tmp = test_functions.split(",", QString::SkipEmptyParts);
         QStringList::const_iterator e = tmp.begin(),ende = tmp.end();
 
         for(; e!=ende;++e)
         {
             std::map<QString, Selectors::TransferTestfunction>
             ::
             const_iterator result = prm_name2enum.find(*e);
 
             if( result!= prm_name2enum.end() )
                 transfer_tests[result->first] = result->second;
 
         }
 
         if (!tmp.empty() && transfer_tests.empty())
             std::cerr << "WARNING : NO VALID TEST FUNCTIONS FOR GRID TRANSFER TESTS SELECTED!!! "<<
                          "CHECK prm file." << std::endl;
 
     }

Klasse: CUDAUnitTestDriver

Diese Klasse steuert die host-device-Kommunikation, also Datentransfer und wann welcher Kernel aufgerufen wird. Die Dokumentation der member-Funktionen steht bei und in der Implementierung, d.h. im cu-file.

 template<typename T>
 class CUDAUnitTestDriver {
 
     const SimParam * __params;
 
     public:
 
         typedef typename blas_pp<T,cublas>::Vector Vector;
 
         CUDAUnitTestDriver(const SimParam &p)
             :
             __params(&p)
         {
             Vector::blas_wrapper_type::Init();
             cudaThreadSynchronize();
         }
 
     ~CUDAUnitTestDriver() { Vector::blas_wrapper_type::Shutdown(); }

Functions for unit tests

     void test_coarse_CG_solver();
 
     void test_gauss_seidel();
 
     void test_grid_transfer();
 
     void test_grid_transfer_implementation(Selectors::TransferTestfunction test_function);
 
     void test_Multigrid();

Class: Potential

This main purpose of this class is to provide some means to copy data back from device to host.

     class Potential : public Vector {
 
         typedef typename Vector::blas_wrapper_type BW;
 
         public:
 
             typedef Vector Base;
 
             Potential() : Vector() {}
             Potential(int n_elements) : Vector(n_elements) {}

Function: print

Copy data back from device to host and dump it to screen.

             void
             print(std::ostream &out) const
             {
                 std::vector<T> tmp(this->__n);
                 T * dst_ptr = &tmp[0];
 
                 const T * src_ptr = this->val();
 
                 BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
                 int dim_x, dim_y;
                 dim_x = pow(this->__n, 1/3.);
 
                 while (dim_x*dim_x*dim_x > this->__n)
                     if (dim_x*dim_x*dim_x > this->__n)
                     --dim_x;
 
                 while (dim_x*dim_x*dim_x < this->__n)
                     if (dim_x*dim_x*dim_x < this->__n)
                         ++dim_x;
 
                 dim_y = dim_x * dim_x;
 
 
                Assert((dim_x*dim_x*dim_x) == this->__n,
                       ::ExcMessage("Bummer"));
 
 
                 for (int i = 0; i < this->__n; i=i+dim_y){
                     out<<std::endl;
                     for (int j = i; j<dim_y+i ; j+=dim_x){
                         out<<std::endl;
 
                         for (int k = j; k<dim_x+j; ++k){
 
                             out<< std::fixed
                              << std::setprecision(3) << tmp[k]<<"  ";
                         }
                     }
                 }
                 out<<std::endl;
                 out<<std::endl;
             }

Function: print_gnu_plot

Copy data back from device to host and print it to file in the form that it can be used by Gnuplot.

             void
             print_gnu_plot(std::ostream &out) const
             {
                 std::vector<T> tmp(this->__n);
                 T * dst_ptr = &tmp[0];
 
                 const T * src_ptr = this->val();
 
                 BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
                 T dim_x, dim_2;
                 dim_x = pow(this->__n,1/3.);
                 / *dim_x++;* /
                 dim_2 = pow(dim_x,2);
 
                 / * for (int i = 0; i < this->__n; i++){
                    out<<tmp[i]<<"\n";
                 }* /
 
                dim_x = (int)dim_x+1;
                dim_2 = (int)dim_2+1;
                out<< "#" << dim_x<<std::endl;
                out<< "#" << dim_2<<std::endl;
                out<< "#" << this->__n<<std::endl;
 
                 for (int i = 0; i < this->__n; i=i+dim_2){
                     out<<std::endl;
                     for (int j = i; j<dim_2+i ; j+=dim_x){
                         out<<std::endl;
 
                         for (int k = j; k<dim_x+j; ++k){
 
                             out<< std::fixed << std::setprecision(6) << tmp[k]<<"\n";
 
                             / *if((k-(int)dim_x-1)%(int)dim_2 == 0){
                                out<<tmp[k]<<" ";
                              }
                             out<<tmp[k]<<" ";* /
 
                         }
                     }
                 }
                 out<<std::endl;
                 out<<std::endl;
             }

Function: print_transfer

Copy data back from device to host and dump the output to the screen. Used for unit test purposes. Prints only the part of the vector used by transfer operators

             void
             print_transfer(std::ostream &out, int mesh, int max_level) const
             {
                 std::vector<T> tmp(this->__n);
                 T * dst_ptr = &tmp[0];
 
                 const T * src_ptr = this->val();
 
                 BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
                 int dim_y, dim_z;
                 int sum;
                 int dim_x = mesh;
                 int start = 0;
                 for(int l = 0; l<max_level+1; l++)
                 {
                     if(l==0)
                         dim_x = dim_x;
                     else
                         dim_x =((dim_x-1)*2)+1;
 
                     dim_y = dim_x * dim_x;
                     dim_z = dim_x * dim_x * dim_x;
                     out<< "whole : " << this->__n<<std::endl;
 
                     out<< "dim x : " << dim_x<<std::endl;
                     out<< "dim x * dim y : " << dim_y<<std::endl;
                     out<< "dim x * dim y * dim z : " << dim_z<<std::endl;
 
                     / *Assert((dim_x*dim_x*dim_x) == this->__n,
                            ::ExcMessage("Bummer"));* /
 
 
 
                      out<<std::endl;
                      out<<std::endl;
 
                     for (int i = start; i<dim_z+start; i=i+dim_y){
 
                         out<<std::endl;
                         for (int j = i; j<dim_y+i ; j+=dim_x){
                             out<<std::endl;
 
                             for (int k = j; k<dim_x+j; ++k){
 
                                 out<< std::fixed
                                  << std::setprecision(3) << tmp[k]<<"  ";
                             }
 
 
                         }
                     }
                     out<<std::endl;
                     / *start* /
                     start += dim_z;
 
 
                 }
             }

Function: print_multigrid_gnu

Copy data back from device to host and print the output to the file. Used by the whole MG-algoritm

             void
             print_multigrid_gnu(std::ostream &out, int mesh, int max_level) const
             {
                 std::vector<T> tmp(this->__n);
                 T * dst_ptr = &tmp[0];
 
                 const T * src_ptr = this->val();
 
                 BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
                 int dim_y, dim_z;
 
                 int dim_x = mesh;
                 int start = 0;
                 for(int l = 0; l<=max_level; l++)
                 {
                     if(l==0)
                         dim_x = dim_x;
                     else
                         dim_x =((dim_x-1)*2)+1;
 
                     dim_y = dim_x * dim_x;
                     dim_z = dim_x * dim_x * dim_x;
                     out<< "#whole : " << this->__n<<std::endl;
 
                     out<< "#dim x : " << dim_x<<std::endl;
                     out<< "#dim x * dim y : " << dim_y<<std::endl;
                     out<< "#dim x * dim y * dim z : " << dim_z<<std::endl;
 
                     / *Assert((dim_x*dim_x*dim_x) == this->__n,
                            ::ExcMessage("Bummer"));* /
 
 
                      out<<std::endl;
                      out<<std::endl;
 
                     for (int i = start; i<dim_z+start; i=i+dim_y){
                         out<<std::endl;
                         for (int j = i; j<dim_y+i ; j+=dim_x){
                             out<<std::endl;
 
                             for (int k = j; k<dim_x+j; ++k){
                                 if(l == max_level)
                                     out<< std::fixed
                                         << std::setprecision(6) << tmp[k]<<"\n";
                             }
                         }
                     }
                     out<<std::endl;
                     start += dim_z;
 
 
                 }
             }
 
 
 
         private:
 
             Potential(const Potential& / *other* /) {}
 
             Potential & operator = (const Potential& / *other* /) {}
         };
 
 
 private:
 
     Potential phi;
     Potential e_H;
 
 };

Klasse: CUDADriver

Diese Klasse steuert die host-device-Kommunikation, also Datentransfer und wann welcher Kernel aufgerufen wird. Die Dokumentation der member-Funktionen steht bei und in der Implementierung, d.h. im cu-file.

 template<typename T>
 class CUDADriver {
 
     const SimParam * __params;
 
 public:
 
     typedef typename blas_pp<T,cublas>::Vector Vector;
 
     CUDADriver(const SimParam &p)
         :
         __params(&p)
     {
         Vector::blas_wrapper_type::Init();
         cudaThreadSynchronize();
     }
 
     ~CUDADriver() { Vector::blas_wrapper_type::Shutdown(); }
 
 
     void coarse_CG_solver();

Class: Potential

This main purpose of this class is to provide some means to copy data back from device to host.

     class Potential : public Vector {
 
         typedef typename Vector::blas_wrapper_type BW;
 
     public:
 
         typedef Vector Base;
 
         Potential() : Vector() {}
         Potential(int n_elements) : Vector(n_elements) {}

Function: print

Copy data back from device to host and dump it to screen.

         void
                 print(std::ostream &out) const
         {
             std::vector<T> tmp(this->__n);
             T * dst_ptr = &tmp[0];
 
             const T * src_ptr = this->val();
 
             BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
             int dim_x, dim_y;
             dim_x = pow(this->__n, 1/3.);
 
             while (dim_x*dim_x*dim_x > this->__n)
                 if (dim_x*dim_x*dim_x > this->__n)
                     --dim_x;
 
             while (dim_x*dim_x*dim_x < this->__n)
                 if (dim_x*dim_x*dim_x < this->__n)
                     ++dim_x;
 
             dim_y = dim_x * dim_x;
 
 
             Assert((dim_x*dim_x*dim_x) == this->__n,
                    ::ExcMessage("Bummer"));
 
 
             for (int i = 0; i < this->__n; i=i+dim_y){
                 out<<std::endl;
                 for (int j = i; j<dim_y+i ; j+=dim_x){
                     out<<std::endl;
 
                     for (int k = j; k<dim_x+j; ++k){
 
                         out<< std::fixed
                                 << std::setprecision(3) << tmp[k]<<"  ";
                     }
                 }
             }
             out<<std::endl;
             out<<std::endl;
         }

Function: print_gnu_plot

Copy data back from device to host and print it to file in the form that it can be used by Gnuplot.

         void
                 print_gnu_plot(std::ostream &out) const
         {
             std::vector<T> tmp(this->__n);
             T * dst_ptr = &tmp[0];
 
             const T * src_ptr = this->val();
 
             BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
             T dim_x, dim_2;
             dim_x = pow(this->__n,1/3.);
             / *dim_x++;* /
             dim_2 = pow(dim_x,2);
 
             / * for (int i = 0; i < this->__n; i++){
                out<<tmp[i]<<"\n";
             }* /
 
             dim_x = (int)dim_x+1;
             dim_2 = (int)dim_2+1;
             out<< "#" << dim_x<<std::endl;
             out<< "#" << dim_2<<std::endl;
             out<< "#" << this->__n<<std::endl;
 
             for (int i = 0; i < this->__n; i=i+dim_2){
                 out<<std::endl;
                 for (int j = i; j<dim_2+i ; j+=dim_x){
                     out<<std::endl;
 
                     for (int k = j; k<dim_x+j; ++k){
 
                         out<< std::fixed << std::setprecision(6) << tmp[k]<<"\n";
 
                         / *if((k-(int)dim_x-1)%(int)dim_2 == 0){
                            out<<tmp[k]<<" ";
                          }
                         out<<tmp[k]<<" ";* /
 
                     }
                 }
             }
             out<<std::endl;
             out<<std::endl;
         }

Function: print_transfer

Copy data back from device to host and dump the output to the screen. Used for unit test purposes. Prints only the part of the vector used by transfer operators

         void
                 print_transfer(std::ostream &out, int mesh, int max_level) const
         {
             std::vector<T> tmp(this->__n);
             T * dst_ptr = &tmp[0];
 
             const T * src_ptr = this->val();
 
             BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
             int dim_y, dim_z;
             int sum;
             int dim_x = mesh;
             int start = 0;
             for(int l = 0; l<max_level+1; l++)
             {
                 if(l==0)
                     dim_x = dim_x;
                 else
                     dim_x =((dim_x-1)*2)+1;
 
                 dim_y = dim_x * dim_x;
                 dim_z = dim_x * dim_x * dim_x;
                 out<< "whole : " << this->__n<<std::endl;
 
                 out<< "dim x : " << dim_x<<std::endl;
                 out<< "dim x * dim y : " << dim_y<<std::endl;
                 out<< "dim x * dim y * dim z : " << dim_z<<std::endl;
 
                 / *Assert((dim_x*dim_x*dim_x) == this->__n,
                        ::ExcMessage("Bummer"));* /
 
 
 
                 out<<std::endl;
                 out<<std::endl;
 
                 for (int i = start; i<dim_z+start; i=i+dim_y){
 
                     out<<std::endl;
                     for (int j = i; j<dim_y+i ; j+=dim_x){
                         out<<std::endl;
 
                         for (int k = j; k<dim_x+j; ++k){
 
                             out<< std::fixed
                                     << std::setprecision(3) << tmp[k]<<"  ";
                         }
 
 
                     }
                 }
                 out<<std::endl;
                 / *start* /
                 start += dim_z;
 
 
             }
         }

Function: print_multigrid_gnu

Copy data back from device to host and print the output to the file. Used by the whole MG-algoritm

         void
                 print_multigrid_gnu(std::ostream &out, int mesh, int max_level) const
         {
             std::vector<T> tmp(this->__n);
             T * dst_ptr = &tmp[0];
 
             const T * src_ptr = this->val();
 
             BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
             int dim_y, dim_z;
 
             int dim_x = mesh;
             int start = 0;
             for(int l = 0; l<=max_level; l++)
             {
                 if(l==0)
                     dim_x = dim_x;
                 else
                     dim_x =((dim_x-1)*2)+1;
 
                 dim_y = dim_x * dim_x;
                 dim_z = dim_x * dim_x * dim_x;
                 out<< "#whole : " << this->__n<<std::endl;
 
                 out<< "#dim x : " << dim_x<<std::endl;
                 out<< "#dim x * dim y : " << dim_y<<std::endl;
                 out<< "#dim x * dim y * dim z : " << dim_z<<std::endl;
 
                 / *Assert((dim_x*dim_x*dim_x) == this->__n,
                        ::ExcMessage("Bummer"));* /
 
 
                 out<<std::endl;
                 out<<std::endl;
 
                 for (int i = start; i<dim_z+start; i=i+dim_y){
                     out<<std::endl;
                     for (int j = i; j<dim_y+i ; j+=dim_x){
                         out<<std::endl;
 
                         for (int k = j; k<dim_x+j; ++k){
                             if(l == max_level)
                                 out<< std::fixed
                                         << std::setprecision(6) << tmp[k]<<"\n";
                         }
                     }
                 }
                 out<<std::endl;
                 start += dim_z;
 
 
             }
         }
 
 
 
     private:
 
         Potential(const Potential& / *other* /) {}
 
         Potential & operator = (const Potential& / *other* /) {}
     };
 
 
 private:
 
     Potential phi;
     Potential e_H;
 
 };
 
 } // namespace step12 END
 
 #endif // CUDADriver_STEP_12_H
 
 
 
 #ifndef CUDA_DRIVER_STEP_12_HH
 #define CUDA_DRIVER_STEP_12_HH
 #include "cuda_driver_step-12.h"
 #include <fstream>
 
 #include <QString>
 
 #include <base/timer.h>
 
 #include <base/CUDATimer.h>
 #include <base/convergence_table.h>

Declarations of kernel wrapper functions

 #include "cuda_kernel_wrapper_step-12.cu.h"
 #include <cutil_inline.h>

Funktion: test_coarse_CG_solver()

Test of the coarse grid solver.

 template<typename T>
 void step12::CUDAUnitTestDriver<T>::test_coarse_CG_solver()
 {
     int n_intervals_per_dim = MESH_DIM-1;
     int n_points_per_dim = n_intervals_per_dim+1;
     int n_points = n_points_per_dim * n_points_per_dim * n_points_per_dim;
 
     Potential reference_solution;
 
 
 
     ::ConvergenceTable convergence_history;
 
     for (int iter = 1; iter < coarse_cg_max_iter; iter++)
     {
         phi.reinit(n_points);
 
         {
             std::vector<T> tmp(n_points);

For testing the correctness of the solver we generate a kind-of random reference solution ...

             for (int k = 0; k < n_points; k++)
                 tmp[k] = 1 + std::sin(k);

... and copy it to the device.

             typename Potential::Base & rs_ref = reference_solution;
             rs_ref = tmp;
 
 
             int x, y, z;

Now, set the interior points to zero ...

             for (int i = 0; i < n_points; i++)
             {
                 x = i%n_points_per_dim;
                 y = (i%(n_points_per_dim*n_points_per_dim))/n_points_per_dim;
                 z = i/(n_points_per_dim * n_points_per_dim);
 
                 bool boundary =    (x == 0) || (x == n_intervals_per_dim)
                                    || (y == 0) || (y == n_intervals_per_dim)
                                    || (z == 0) || (z == n_intervals_per_dim);
 
                 if (!boundary)
                     tmp[i] = 0;
             }

and use this as initial condition by putting it into the solution vector.

             typename Potential::Base & ref = phi;
             ref = tmp;
 
             phi.print(std::cout);
         }
 
         if(print_sols){
         std::cout
                 << "||Phi_ref||_2 : " << reference_solution.l2_norm()
                 << std::endl;
         }
         if(print_sols) {
             std::cout
                     << "Phi_ref : " << std::endl;
             reference_solution.print(std::cout);
         }
 
         if(print_sols){
         std::cout
                 << "||Phi_0||_2 : " << phi.l2_norm()
                 << std::endl;
         std::cout << "Phi_0: \n\n";
         }
 
         if(print_sols)
             phi.print(std::cout);
 
         T tolerance = cg_tol;

store r_k_1, alpha, beta in one array

         typename Potential::Base residual(7*coarse_cg_max_iter+2);
         {
             std::vector<T> tmp(residual.size(), 0.);
             residual = tmp;
         }
 
 
         CUDATimer cg_timer;
         coarse_grid_CG_solve_unit_test(phi.array().val(),
                                        n_points_per_dim,
                                        tolerance,
                                        iter,
                                        residual.array().val());
 
         if(print_sols)
             cg_timer.print_elapsed("Time spent in coarse grid solve : ");
 
         if(print_sols)
             std::cout<<  "||Phi_final||_2 : " << phi.l2_norm()<<std::endl;
 
         if(print_sols){
         std::cout
                 << "N Threads : " << N_COARSE_GRID_THREADS
                 << ", N elements : " << phi.size()
                 << ", Residuals: \n\n" << std::setprecision(10);

residual.print();

         std::cout << "Phi: \n\n";
         }
 
         if(print_sols)
             phi.print(std::cout);

Compare solutions.

         phi -= reference_solution;
 
         if(print_sols)
             std::cout << "Phi_final - Phi_ref: \n\n";
 
         if(print_sols)
             phi.print(std::cout);
 
         double l2_abs_error = phi.l2_norm();
 
         double l2_rel_error = l2_abs_error / reference_solution.l2_norm();
 
         if(print_sols){

print convergence summary

         std::cout<<  "||Phi_final - Phi_ref||_2 : " << std::setprecision(10)
                 << l2_abs_error
                 << "\n"
                 << "||Phi_final - Phi_ref||_2 / ||Phi_ref||_2 : "
                 << l2_rel_error
                 << std::endl;
 
         convergence_history.add_value("# iter", iter);
 
         convergence_history.add_value("||u - u_h||_2", double(l2_abs_error) );
         convergence_history.set_precision        ("||u - u_h||_2", 16);
         convergence_history.add_value("||u - u_h||_2/||u||_2", double(l2_rel_error) );
         convergence_history.set_precision        ("||u - u_h||_2/||u||_2", 16);
 
         }
     }
 
     {
 
         QString filename = "unit_test_coarse_grid_cg_";
 
         int np = N_POINTS_PHI;
         filename += QString::number(np);
         filename += "_points.dat";
         std::ofstream out(filename.toAscii());
 
         convergence_history.write_text(out);
     }
 
     {
         std::ofstream out("phi_out_coarse.dat");
         phi.print_gnu_plot(out);
     }
 }

Funktion: coarse_CG_solver()

Running the coarse grid solver.

 template<typename T>
 void step12::CUDADriver<T>::coarse_CG_solver()
 {
     int n_intervals_per_dim = MESH_DIM-1;
     int n_points_per_dim = n_intervals_per_dim+1;
     int n_points = n_points_per_dim * n_points_per_dim * n_points_per_dim;

system size

     T L = 1.;

radius of charged sphere

     T R = .3;

cell size

     T h = L/n_intervals_per_dim;
 
 
     phi.reinit(n_points);
     {

As initial solution we use a vector containing zeros

         std::vector<T> tmp(n_points, 0.);

... and copy it to the device.

         typename Potential::Base & ref = phi;
         ref = tmp;
     }
 
 
     T tolerance = cg_tol;

store r_k_1, alpha, beta in one array

     typename Potential::Base residual(7*coarse_cg_max_iter+2);
     {
         std::vector<T> tmp(residual.size(), 0.);
         residual = tmp;
     }
 
     coarse_grid_CG_solve(phi.array().val(), n_points_per_dim, tolerance,
                          R, h,
                          coarse_cg_max_iter,
                          residual.array().val());
 
     std::ofstream out("phi_out_coarse.dat");
     phi.print_gnu_plot(out);
 }

Funktion: test_gauss_seidel

This function calls the kernel gauss_seidel

 template<typename T>
 void step12::CUDAUnitTestDriver<T>::test_gauss_seidel()
 {
     int n_intervals_per_dim = MESH_DIM-1;
     int n_points_per_dim = n_intervals_per_dim+1;
     int n_points = n_points_per_dim * n_points_per_dim * n_points_per_dim;
 
 
     static const bool  print_sols = false;
     static const int max_iter = 50;
     static const double tol = 1e-12;

system size

     T L = 1.;

radius of charged sphere

     T R = .25;
 
     T h = L/n_intervals_per_dim;
 
     Potential reference_solution, sol_diff;
 
     ::ConvergenceTable convergence_history;
 
     std::vector<T> sol_ref_host(n_points);
     phi.reinit(n_points);
     e_H.reinit(n_points);
     {
         std::vector<T> tmp(n_points);

For testing the correctness of the solver we generate a kind-of random reference solution ...

         for (int k = 0; k < n_points; k++)
         {
             sol_ref_host[k] = 1 + std::sin(k);

sol_ref_host[k] = std::exp(1/k);

             tmp[k] =  sol_ref_host[k];
         }

... and copy it to the device.

         typename Potential::Base & rs_ref = reference_solution;
         rs_ref = sol_ref_host;
 
         int x, y, z;

Now, set the interior points to zero ...

         for (int i = 0; i < n_points; i++)
         {
             x = i%n_points_per_dim;
             y = (i%(n_points_per_dim*n_points_per_dim))/n_points_per_dim;
             z = i/(n_points_per_dim * n_points_per_dim);
 
             bool boundary =    (x == 0) || (x == n_intervals_per_dim)
                                || (y == 0) || (y == n_intervals_per_dim)
                                || (z == 0) || (z == n_intervals_per_dim);
 
             if (!boundary)
                 tmp[i] = 0;
         }

and use this as initial condition by putting it into the solution vector.

         typename Potential::Base & ref = phi;
         ref = tmp;
     }
 
     std::cout
             << "||Phi_ref||_2 : " << reference_solution.l2_norm()
             << std::endl;
 
     if(print_sols) {
         std::cout
                 << "Phi_ref : " << std::endl;
         reference_solution.print(std::cout);
     }
 
     std::cout
             << "||Phi_0||_2 : " << phi.l2_norm()
             << std::endl;
     std::cout << "Phi_0: \n\n";
 
     if(print_sols)
         phi.print(std::cout);
 
     T tolerance = tol;

store r_k_1, alpha, beta in one array

     typename Potential::Base residual(7*coarse_cg_max_iter+2);
     {
         std::vector<T> tmp(residual.size(), 0.);
         residual = tmp;
     }
     double l2_abs_error; double l2_rel_error;
 
     CUDATimer gaus_seidel_timer;
     for (int iter = 0; iter < max_iter; iter++)
     {
         gauss_seidel_unit_test(phi.array().val(),
                                n_intervals_per_dim,
                                R,
                                h
                                );
         typename Potential::Base & sol_diff_ref = sol_diff;
         sol_diff_ref = sol_ref_host;
 
         / *sol_diff = phi;* /
         sol_diff -= phi; // reference_solution;
 
         l2_abs_error = sol_diff.l2_norm();
 
         l2_rel_error  = l2_abs_error / reference_solution.l2_norm();
 
         convergence_history.add_value("# iter", iter);
 
         convergence_history.add_value("||u - u_h||_2", double(l2_abs_error) );
         convergence_history.set_precision        ("||u - u_h||_2", 16);
         convergence_history.add_value("||u - u_h||_2/||u||_2", double(l2_rel_error) );
         convergence_history.set_precision        ("||u - u_h||_2/||u||_2", 16);
     }
 
     MG_reference_solution(e_H.array().val(),phi.array().val(),
                           n_intervals_per_dim,
                           h,
                           0.25,
                           true);
 
     gaus_seidel_timer.print_elapsed("Time spent in seidel grid solve : ");
 
     {
         std::ofstream out("phi_out_seidel.dat");
         phi.print_gnu_plot(out);
     }
 
     {
         std::ofstream out("phi_out_seidel_reference.dat");
         e_H.print_gnu_plot(out);
     }
 
     std::cout<<  "||Phi_final||_2 : " << phi.l2_norm()<<std::endl;
 
     std::cout
             << "N Threads : " << N_COARSE_GRID_THREADS
             << ", N elements : " << phi.size();
 
 
 
     std::cout << "Phi: \n\n";
 
     if(print_sols)
         phi.print(std::cout);

Compare solutions.

     phi -= reference_solution;
 
     std::cout << "Phi_final - Phi_ref: \n\n";
 
     if(print_sols)
         phi.print(std::cout);

print convergence summary

     std::cout<<  "||Phi_final - Phi_ref||_2 : " << std::setprecision(10)
              << l2_abs_error
              << "\n"
              << "||Phi_final - Phi_ref||_2 / ||Phi_ref||_2 : "
              << l2_rel_error
              << std::endl;
 
     {
 
         QString filename = "unit_test_gauss_seidel_";
 
         int np = N_POINTS_PHI;
         filename += QString::number(np);
         filename += "_points.dat";
         std::ofstream out(filename.toAscii());
 
         convergence_history.write_text(out);
     }
 
 
      std::cout<<  "||Error_final||_2 : " << e_H.l2_norm()<<std::endl;
 
 
 }

Funktion: test_Multigrid()

The function tests the whole multigrid algorithm

 template<typename T>
 void step12::CUDAUnitTestDriver<T>::test_Multigrid()
 {
 
     int ncycle = 1;
     int max_level = 1;
 
     int max_iter = 50;
 
     int n_intervals_per_dim;
     int  back;
     bool prolongation;
     int n_points = MESH_DIM * MESH_DIM * MESH_DIM;
     int start_n_points = n_points;
     T tolerance = cg_tol;
     int start_intervals_per_dim = MESH_DIM-1;
     int max_intervals_per_dim = start_intervals_per_dim;
     int last_interval = start_intervals_per_dim;
     int max_n_points = n_points;
 
     for(int i = 0; i<max_level; i++)
     {
         last_interval = last_interval * 2;
         max_intervals_per_dim =last_interval;
         max_n_points += (max_intervals_per_dim+1)
                         *(max_intervals_per_dim+1)
                         *(max_intervals_per_dim+1);
     }
 
 
 
     T * u_h;
     T * u_H;
     T * diff;
     T * e_h;

system size

     T L = 1.;

radius of charged sphere

     T sigma = .25;
     T R = .25;
 
     T h = L/start_intervals_per_dim;
 
     printf("whole phi -->  %d\n",max_n_points);
 
     phi.reinit(max_n_points);
     e_H.reinit(max_n_points);
 
     phi *= 0;
     cudaThreadSynchronize();
 
     typename Potential::Base residual(7*coarse_cg_max_iter+2);
     {
         std::vector<T> tmp(residual.size(), 0.);
         residual = tmp;
     }
     u_h = phi.array().val();
     u_H = phi.array().val();
     diff= phi.array().val();
     e_h = e_H.array().val();
 
     n_intervals_per_dim = start_intervals_per_dim;

Start of the multigrid

     for (int level = 0; level <=max_level; level++)
     {
         for(int n_cycle = ncycle; n_cycle > 0; n_cycle--)
         {
             u_h = phi.array().val();
             u_H = phi.array().val();
             n_points = start_n_points;

go up

             for(int up = 1; up <=level; up++)
             {
                 prolongation = true;
 
                 u_H = u_h;
                 u_h +=n_points;
 
 
                 n_intervals_per_dim *= 2 ;
                 h = L/n_intervals_per_dim;

prolongate

                 grid_transfer(u_H, u_h, n_intervals_per_dim, prolongation);
 
                 n_points = (n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1);
 
                 for(int g = 0; g<max_iter; g++)
                     gauss_seidel(u_h, n_intervals_per_dim,h,sigma);
 
                 printf("UPgauss(%d) ", n_points);
                 printf("--> Pro  u_H --> %d , u_h --> %d  \n", u_H-diff, u_h - diff);
 
             }

go down

             for(int down = level; down >0 ; down--)
             {
                 prolongation = false;

restriction

                 n_intervals_per_dim /= 2 ;
                 back = n_intervals_per_dim /2;
                 h = L/n_intervals_per_dim;
 
                 grid_transfer(u_H, u_h, n_intervals_per_dim, prolongation);
 
                 n_points = (n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1);
 
 
                 if(down == 1){
                     printf("\ncg(%d)-->", n_points);
                     printf("Restr  u_H --> %d , u_h --> %d\n", u_H-diff, u_h-diff);
 
 
 
                     coarse_grid_CG_solve(phi.array().val(), MESH_DIM, tolerance, sigma, h,
                                          coarse_cg_max_iter,
                                          residual.array().val());
 
                 }
                 else{
                     printf("DOWNgauss(%d) --> ", n_points);
                     printf("Restr  u_H --> %d , u_h --> %d\n", u_H-diff, u_h-diff);
 
                     for(int g = 0; g<max_iter; g++)
                         gauss_seidel(u_H, n_intervals_per_dim,h,sigma);
                 }
 
                 u_h = u_H;
                 u_H -=((back+1)*(back+1)*(back+1)) ;
 
             }
 
             if(level == 0 && !(level == 0 && n_cycle != ncycle)){
 
                  coarse_grid_CG_solve(phi.array().val(), MESH_DIM, tolerance, sigma, h,
                                      coarse_cg_max_iter,
                                      residual.array().val());
 
                 printf("cg(%d) ", n_points);
                 printf("First u_H --> %d , u_h --> %d\n", u_H-diff, u_h-diff);
             }
 
             printf("\n");
         }
 
     }
     n_points = start_n_points;
     u_h = phi.array().val();
     n_intervals_per_dim=start_intervals_per_dim;

go up

     for(int level = 1; level <=max_level; level++)
     {
         u_H = u_h;
         prolongation = true;
         n_intervals_per_dim *= 2 ;
         h = L/n_intervals_per_dim;

prolongate

         grid_transfer(u_h, u_H, n_intervals_per_dim, prolongation);
 
 
         u_h +=n_points;
         e_h +=n_points;
 
         n_points = (n_intervals_per_dim+1)
                    *(n_intervals_per_dim+1)
                    *(n_intervals_per_dim+1);
 
         printf("end_gauss(%d) ", n_points);
         printf("--> Pro  U_H --> %d , U_h --> %d \n", u_H-diff, u_h-diff);
 
         for(int g = 0; g<max_iter; g++)
             gauss_seidel(u_h, n_intervals_per_dim,h,sigma);
     }
     printf("\n");

true -> reference solution false -> error

     bool reference_or_error;
     reference_or_error = true;

reference_or_error = false;

     MG_reference_solution(e_h,u_h,n_intervals_per_dim,h,sigma,reference_or_error);
 
     / *std::cout<<phi.l2_norm()<<std::endl;* /

phi.print(std::cout);

phi.print_transfer(std::cout, MESH_DIM, max_level ); e_H.print_transfer(std::cout, MESH_DIM, max_level );

     std::ofstream out("phi_multi_out.dat");
     phi.print_multigrid_gnu(out, MESH_DIM, max_level);
 
     if(reference_or_error)
     {
         std::ofstream out2("phi_multi_out_reference.dat");
         e_H.print_multigrid_gnu(out2, MESH_DIM, max_level);
 
     }else
     {
         std::ofstream out2("phi_multi_out_error.dat");
         e_H.print_multigrid_gnu(out2, MESH_DIM, max_level);
 
         std::cout<<  "||Final_Error||_2 : " << e_H.l2_norm()<<std::endl;
 
     }
 
 
 
 
 
 }

Funktion: test_grid_transfer()

The function iterates over the testing parameters and calls the grid_grid_transfer_implementation with chosen parameter

 template<typename T>
 void step12::CUDAUnitTestDriver<T>::test_grid_transfer()
 {
     if (this->__params->transfer_tests.empty())
     {
         std::cout << __FUNCTION__ << ": nothing to be done.\n";
         return;
     }
 
     std::map<QString, Selectors::TransferTestfunction>::const_iterator tf=this->__params->transfer_tests.begin();
 
     for(; tf!=this->__params->transfer_tests.end(); ++tf)
     {
         std::cout << "Testing function : " << tf->first.toStdString() << std::endl;
         this->test_grid_transfer_implementation(tf->second);
     }
 }

Funktion: test_grid_transfer_implementation

The function tests transfer operators It calls prolongation_unit_test and restriction unit_test

 template<typename T>
 void  step12::CUDAUnitTestDriver<T>::test_grid_transfer_implementation(Selectors::TransferTestfunction test_function)
 {
 
     int ncycle = 1;
     if(this->__params->n_cycle == "v")
         ncycle = 1;
     else if(this->__params->n_cycle == "w")
         ncycle = 2;
 
     int max_level = this->__params->max_level+1;
 
     int n_intervals_per_dim;
     int  back;
     bool prolongation;
     int n_points = MESH_DIM * MESH_DIM * MESH_DIM;
     int start_n_points = n_points;
     int start_intervals_per_dim = MESH_DIM-1;
     int max_intervals_per_dim = start_intervals_per_dim;
     int last_interval = start_intervals_per_dim;
     int max_n_points = n_points;
     int restriction_first_n_points,first_n_intervals_per_dim;
 
 
     for(int i = 0; i<max_level; i++)
     {
 
         last_interval = last_interval * 2;
         max_intervals_per_dim =last_interval;
         max_n_points += (max_intervals_per_dim+1)
                         *(max_intervals_per_dim+1)
                         *(max_intervals_per_dim+1);
     }
 
     if(this->__params->disp_mem_consumption)
         std::cout << "Estimated memory consumption of all solutions : " << max_n_points * sizeof(T)/(1024*1024*1024.) << " GByte" << std::endl;
 
     T * u_h;
     T * u_H;
     T * diff;

system size

     T L = 1.;
 
 
 
     T H = L/start_intervals_per_dim;
     if(this->__params->disp_phi_max_size)
         printf("whole phi -->  %d\n\n",max_n_points);
 
     phi.reinit(max_n_points);
 
     phi *= 0;
     cudaThreadSynchronize();
 
     u_h = phi.array().val();
     u_H = phi.array().val();
     diff= phi.array().val();
     n_intervals_per_dim = start_intervals_per_dim;
 
     for (int level = 0; level <max_level; level++)
     {
         if(this->__params->disp_current_level)
             printf("current level ---> %d\n", level);
 
 
         for(int n_cycle = ncycle; n_cycle > 0; n_cycle--)
         {
             u_h = phi.array().val();
             u_H = phi.array().val();
 
             n_points = start_n_points;
             n_intervals_per_dim = start_intervals_per_dim;
 
             int current_level = 0; // coarsest level
 
             ::Timer prolongation_timer;
 
             for(int up = 1; up <=level; up++, current_level++)
             {
                 prolongation = true;
 
                 u_H = u_h;
                 u_h +=n_points;
 
                 e_H.reinit(n_points);
 
                 std::vector<T> tmp(n_points,0.);

... and copy it to the device.

                 typename Potential::Base & e_ref = e_H;
                 e_ref = tmp;

prolongate

                 n_intervals_per_dim *= 2 ;
 
                 T h = H/2;

grid_transfer(u_H, u_h, n_intervals_per_dim, R, h, prolongation);

                 prolongation_unit_test(u_H, u_h, e_H.array().val(),
                                        n_intervals_per_dim, h, current_level, test_function);
                 cudaThreadSynchronize();
 
                 if(this->__params->disp_error_matrix)
                     e_H.print(std::cout);
 
                 if(this->__params->disp_pointer)
                     printf("\nPro  u_H --> %d,  u_h --> %d  \n", u_H-diff, u_h - diff);
 
                 if(this->__params->disp_transfer_error)
                     printf("prolongation_error %e \n", e_H.l2_norm() / std::sqrt(e_H.size() ) );
 
                 if(this->__params->disp_transfer_dimension_resize_info)
                     printf("UPtransfer( %d to ", n_points);
 
                 n_points = (n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1);
                 H/=2;
                 if(this->__params->disp_transfer_dimension_resize_info)
                     printf("%d )\n", n_points);
             }
 
 
             if(this->__params->disp_transfer_time)
                 std::cout << "Time elapsed in one prolongation from coarsest to finest grid : "<< prolongation_timer() << "sec." << std::endl;
 
             ::Timer restriction_timer;
             current_level = 0;
             for(int down = level; down >0 ; down--, current_level++)
             {
 
 
                 first_n_intervals_per_dim = n_intervals_per_dim /2;
                 restriction_first_n_points = (first_n_intervals_per_dim+1)
                                              *(first_n_intervals_per_dim+1)
                                              *(first_n_intervals_per_dim+1);
                 e_H.reinit(restriction_first_n_points);
 
                 std::vector<T> tmp(restriction_first_n_points,0.);

... and copy it to the device.

                 typename Potential::Base & e_ref = e_H;
                 e_ref = tmp;
 
 
                 prolongation = false;

Restriction

                 T h = H;
 
                 restriction_unit_test(u_H, u_h, e_H.array().val(),
                                       n_intervals_per_dim, h, current_level, test_function);
 
 
                 cudaThreadSynchronize();
                 if(this->__params->disp_error_matrix)
                     e_H.print(std::cout);
 
                 if(this->__params->disp_pointer)
                     printf("\nRestr  u_H --> %d,  u_h --> %d  \n", u_H-diff, u_h-diff);
 
                 if(this->__params->disp_transfer_error)
                     printf("restriction_error %e \n", e_H.l2_norm() / std::sqrt(e_H.size() ) );
 
                 if(this->__params->disp_transfer_dimension_resize_info)
                     printf("Downtransfer( %d to ", n_points);
 
                 n_intervals_per_dim /= 2 ;
                 n_points = (n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1);
                 H*=2;
                 if(this->__params->disp_transfer_dimension_resize_info)
                     printf("%d )\n", n_points);
 
 
                 u_h = u_H;
                 back = n_intervals_per_dim /2;
                 u_H -=((back+1)*(back+1)*(back+1));
 
 
 
             }
 
 
             if(this->__params->disp_transfer_time)
                 std::cout << "Time elapsed in one restriction from finest to coarsest grid : "<< restriction_timer() << "sec." << std::endl;
         }
 
     }
     printf("\n");
     if(this->__params->disp_data_matrix)
         phi.print_transfer(std::cout, MESH_DIM, max_level-1 );
 
 
     / *std::cout<<phi.l2_norm()<<std::endl;* /
     / *phi.print(std::cout);* /
 
 }
 
 
 
 
 #endif

CUDA_DRIVER_STEP_12_HH

STL header

 #include <iostream>
 #include <vector>
 #include <QString>
 #include <QStringList>
 #include <map>

Treiber fuer den GPU-Teil

 #include "cuda_driver_step-12.h"

deal.II-Komponenten include <lac/vector.h>

 #include <base/parameter_handler.h>

cublas-Wrapper-Klassen. Binden alle sonstigen benoetigten header-Dateien ein.

 #include "cuda_driver_step-12.hh"
 
 namespace step12 {

Class: MyFancySimulation

This class controls the simulation of a physical problem.

     class MyFancySimulation {
 
     public:
 
         MyFancySimulation();
 
         void run_unit_tests();
 
         void run();
 
 
     private:
 
     };
 
 
 }

Constructor: MyFancySimulation

The constructor should comlete the initialization of the simulation.

 step12::MyFancySimulation::MyFancySimulation()
 {
 
 }

Function: run_unit_tests

The function runs the unit tests of chosen functionalities.

 void step12::MyFancySimulation::run_unit_tests()
 {
 
     std::string prm_filename = "unit_tests.prm";
 
     ::ParameterHandler prm_handler;
 
     SimParam::declare(prm_handler);
 
     prm_handler.read_input (prm_filename);
 
     SimParam params;
 
     params.get(prm_handler);
 
     std::ostringstream logfile_name;
 
     logfile_name << prm_filename << ".log";
 
     std::ofstream out(logfile_name.str().c_str());
 
     prm_handler.print_parameters(out, ::ParameterHandler::Text );
 
 #ifdef USE_SINGLE_PRECISION
     step12::CUDAUnitTestDriver<float>  mg_unit_test(params);
 #else
     step12::CUDAUnitTestDriver<double> mg_unit_test(params);
 #endif

mg_unit_test.test_coarse_CG_solver();

mg_unit_test.test_gauss_seidel();

mg_unit_test.test_grid_transfer();

      mg_unit_test.test_Multigrid();
 
     std::cout << "==============   Unit tests Done.   ==============\n\n" << std::endl;
 
 }

Function: run

 void step12::MyFancySimulation::run()
 {
 
 #ifdef USE_SINGLE_PRECISION
     / *step12::CUDADriver<float>  mg_solver(params);* /
 #else
     / *step12::CUDADriver<double> mg_solver(params);* /
 #endif
 
     std::cout << "Fertig.!!!!!!!!!!!!!!!!!!!!" << std::endl;
 }

Function: main

 int main(int / *argc* /, char * / *argv* /[])
 {
     cudaSetDevice(1);
 
     using namespace step12;
     MyFancySimulation machma;
 
     machma.run_unit_tests();
 
     / *machma.run();* /
 }

Results

All classes and functions needed for the Multigrid algorithm to work have been implemented and tested

The Gauss-Seidel Algorithm

The Gauss-Seidel algoritm is used as smoother at each level.

The Conjugate-Gradient Algorithm

The Cg-algorithm converges as it can be seen on ther picture below. The number of iterations needed to reach the prescribed tolerance of 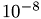$10^{-8}$ depends on the number of unknowns 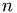$n$. The number of iterations presumably grows like 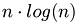$n\cdot log(n)$ . The maximal 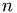$n$ is chosen such that the coarse grid solution and the residual vector fits into the shared memory of one multiprocessor of the graphics card. The number of unknowns is given in the legend on the right-hand side in the figure below. For instance 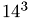$14^{3}$ means that the coarse grid consists of 14 points per spatial dimension, that is 2744 points in total.

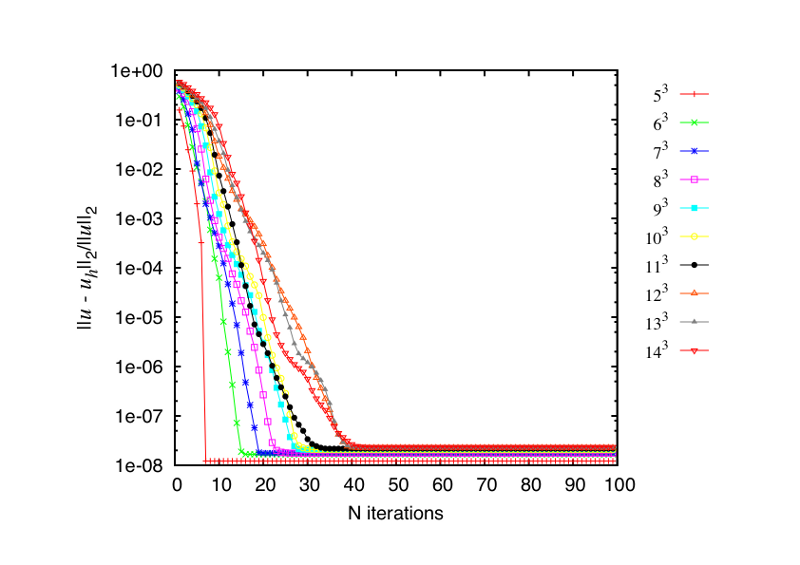
unit_test_coarse_grid_cg_scaled.png

Transfer Operators (prolongation and restriction)

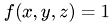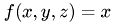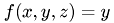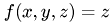Transfer operators are used to transfer data from one level to another. Prolongation and Restriction use multilinear interpolation to transfer. Both algorithms have been tested with the set of functions that can be interpolated exactly. These functions are $f(x,y,z) = 1$, $f(x,y,z) = x$, $f(x,y,z) = y$ and $f(x,y,z) = z$ and all multilinear combinations of them, e.g. 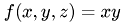$f(x,y,z) = xy$. As expected the Prolongation and Restriction operators produce no error interpolating mentioned functions.

The operations are not computationally intensive. Especially the restriction operator computes less points than it reads. The main problem in implementation of the operators consists of controlling the memory bandwidth. In order to achive the best possible memory bandwith the update of the points should be done in possibly few steps of reading from one dimension and writing into other.

The solution that use shared memory to store the points that are needed to update different points at other dimension should be considered. The memory bandwidth has to be tested soon.

The example of the prolongation

As we can see the interpolation result for the function 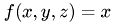$f(x,y,z) = x$ is exact. 



Testing function : one
UPtransfer( 27 to 125 )
prolongation_error 0.000000e+00


1.000  1.000  1.000  
1.000  1.000  1.000  
1.000  1.000  1.000


1.000  1.000  1.000  
1.000  1.000  1.000  
1.000  1.000  1.000


1.000  1.000  1.000  
1.000  1.000  1.000  
1.000  1.000  1.000


1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000


1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000


1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000


1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000


1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  
1.000  1.000  1.000  1.000  1.000  


As expected the result of interpolating the function 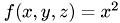$f(x,y,z) = x^{2}$ is not exact anymore 
Testing function : xx
prolongation_error 1.482318e-03


0.000  0.250  1.000  
0.000  0.250  1.000  
0.000  0.250  1.000


0.000  0.250  1.000  
0.000  0.324  1.000  
0.000  0.250  1.000


0.000  0.250  1.000  
0.000  0.250  1.000  
0.000  0.250  1.000


0.000  0.062  0.250  0.562  1.000  
0.000  0.062  0.250  0.562  1.000  
0.000  0.062  0.250  0.562  1.000  
0.000  0.062  0.250  0.562  1.000  
0.000  0.062  0.250  0.562  1.000


0.000  0.062  0.250  0.562  1.000  
0.000  0.114  0.278  0.614  1.000  
0.000  0.119  0.279  0.619  1.000  
0.000  0.114  0.278  0.614  1.000  
0.000  0.062  0.250  0.562  1.000


0.000  0.062  0.250  0.562  1.000  
0.000  0.119  0.279  0.619  1.000  
0.000  0.125  0.281  0.625  1.000  
0.000  0.119  0.279  0.619  1.000  
0.000  0.062  0.250  0.562  1.000


0.000  0.062  0.250  0.562  1.000  
0.000  0.114  0.278  0.614  1.000  
0.000  0.119  0.279  0.619  1.000  
0.000  0.114  0.278  0.614  1.000  
0.000  0.062  0.250  0.562  1.000


0.000  0.062  0.250  0.562  1.000  
0.000  0.062  0.250  0.562  1.000  
0.000  0.062  0.250  0.562  1.000  
0.000  0.062  0.250  0.562  1.000  
0.000  0.062  0.250  0.562  1.000


 

The following parameter file has been used for testing of transfer operators 
# Listing of Parameters
# ---------------------
subsection Grid transfer tests
  # Displaying level of a current multigrid cycle, 0 at the bottom
  set Display current level         = flase


  # Displaying dimensions of the curent reference solution matrix
  set Display dimension information = true


  # Displaying error matrix of one resizing step
  set Display error matrix          = false


  # Displaying grid size of the maximum level
  set Display finest grid size      = flase


  # Displaying memory consumption of all solutions
  set Display memory consumption    = false


  # Displaying begin of the areas within the whole refernce solution vector
  set Display pointers              = false


  # Displaying current reference solution matrix containing actual data
  set Display reference solution    = true


  # Displaying l2 norm of the error vector of one resizing step.
  set Display transfer error        = true


  # Displaying transfer time between two levels
  set Display transfer time         = false


  # Maximum level of multigrid cycles.
  # Possible values : 1,2,3...
  set Max level                     = 2


  # Functions for testing the multigrid transfer. Transfer is done via
  # multilinear interpolation.Test functions comprise the set of functions
  # that can be transferred exactly (all multilinear combinations of one,
  # x,y,z)and several which are quadratic or cubic in one component in order
  # to reproduceinterpolation errors.Possible values : one, x, y, z, xy, xz,
  # yz, xyz, xx, yy, zz, xxyy, xxyz, yyzz, xyyz, xyzz, xyzzz
  set Test functions                = xx


  # Type of Cycle(v,w).Multigrid cycles types defined in Weseling  # Possible
  # values: v,w
  set Type of cycle                 = v
end

  
The plain program



(If you are looking at a locally installed CUDA HPC Praktikum version, then the program can be found at  .. /.. /testsite / /step-12 /step-cu.cc . Otherwise, this is only the path on some remote server.) 
 #ifndef CUDA_KERNEL_STEP_12_CU_H
 #define CUDA_KERNEL_STEP_12_CU_H
 #define TILE_SIZE 6
 #define MESH_DIM 3
 
 #if MESH_DIM==3
 #define N_POINTS_PHI  27
 #elif MESH_DIM==4
 #define N_POINTS_PHI  64
 #elif MESH_DIM==5
 #define N_POINTS_PHI  125
 #elif MESH_DIM==6
 #define N_POINTS_PHI  216
 #elif MESH_DIM==7
 #define N_POINTS_PHI  343
 #elif MESH_DIM==8
 #define N_POINTS_PHI  512
 #elif MESH_DIM==9
 #define N_POINTS_PHI  729
 #elif MESH_DIM==10
 #define N_POINTS_PHI 1000
 #elif MESH_DIM==11
 #define N_POINTS_PHI 1331
 #elif MESH_DIM==12
 #define N_POINTS_PHI 1728
 #elif MESH_DIM==13
 #define N_POINTS_PHI 2197
 #elif MESH_DIM==14
 #define N_POINTS_PHI 2744
 #endif
 
 #define N_COARSE_GRID_THREADS 256
 
 
 static const bool print_sols        = false;
 static const int coarse_cg_max_iter = 100;
 static const double cg_tol          = 1e-12;
 
 struct Selectors {
 
     enum TransferTestfunction { one,
                                 x, y, z,
                                 xy, xz, yz,
                                 xyz,
                                 xx, yy, zz,
                                 xxyy, xxyz, yyzz,
                                 xyyz, xyzz, xyzzz };
 
 };

  
 void coarse_grid_CG_solve_unit_test(float* phi, int n_coarse_points_per_dim,
                                     float tolerance,
                                     int max_iter,
                                     float* residual);
 
 void coarse_grid_CG_solve(float* phi,
                           int n_coarse_points_per_dim,
                           float tolerance,
                           float R,
                           float h,
                           int max_iter,
                           float * residual);
 
 void gauss_seidel(float* phi,
                   int n_intervals_per_dim,
                   float R,
                   float h);
 
 void grid_transfer(float* phi,
                    float* test,
                    int n_intervals_per_dim,
                    bool prolongation);
 
 void MG_reference_solution(float* e_h,
                            float* u_h,
                            int n_intervals_per_dim,
                            float h,
                            float sigma,
                            bool reference_or_error);
 
 
 #ifndef USE_SINGLE_PRECISION
 
 void coarse_grid_CG_solve_unit_test(double* phi, int n_coarse_points_per_dim,
                                     double tolerance,
                                     int max_iter,
                                     double* residual);
 
 void coarse_grid_CG_solve(double* phi, int n_coarse_points_per_dim,
                           double tolerance, double R, double h,
                           int max_iter,
                           double * residual);
 
 void gauss_seidel(double* phi,
                   int n_intervals_per_dim,
                   double R,
                   double h);
 
 void gauss_seidel_unit_test(double* phi,
                   int n_intervals_per_dim,
                   double R,
                   double h);
 
 void grid_transfer(double* phi,
                    double * test,
                    int n_intervals_per_dim,
                    bool prolongation);
 
 void prolongation_unit_test( double * u_H, double * u_h, double* e_H,
                              int n_intervals_per_dim, double h, int current_level,
                              Selectors::TransferTestfunction ftest);
 
 void restriction_unit_test( double * u_H, double * u_h, double* e_H,
                             int n_intervals_per_dim, double h, int current_level,
                             Selectors::TransferTestfunction ftest);
 
 
 void MG_reference_solution(double* e_h, double* u_h,
                            int n_intervals_per_dim,
                            double h,
                            double sigma,
                            bool reference_or_error);
 #endif
 
 #endif // CUDA_KERNEL_STEP_12_CU_H
 
 
 
 #include <cutil_inline.h>
 #include <cuda_kernel_wrapper_step-12.cu.h>
 
 #define RED_BLACK_DEBUG
 #undef  RED_BLACK_DEBUG
 
 #define RHS_DEBUG
 #undef  RHS_DEBUG

  
  
 template <typename T>
 class Constant{
 
 public:
     typedef  T NumberType;
     __device__ Constant(){}
 
     __forceinline__ __device__
     const T operator ()(const T x, const T y ,const T z) const
     {
         return 1;
     }
 
 };

  
 template <typename T>
 class X{
 
 public:
     typedef  T NumberType;
     __device__ X(){}
 
     __forceinline__ __device__
     const T operator ()(const T x, const T y ,const T z) const
     {
 
         return x;
     }
 };

  
 template <typename T>
 class Y{
 
 public:
     typedef  T NumberType;
     __device__ Y(){}
 
     __forceinline__ __device__
     const T operator ()(const T x, const T y ,const T z) const
     {
 
         return y;
     }
 
 };

  
 template <typename T>
 class Z{
 
 public:
      typedef  T NumberType;
 
     __device__ Z(){}
 
     __forceinline__ __device__
     const T operator ()(const T x, const T y ,const T z) const
     {
 
         return z;
     }
 };

  
 template<typename FX, typename FY, typename FZ>
 class F{
 
 public:
 
     typedef typename FX::NumberType NumberType;
     typedef typename FX::NumberType T;
 
     __device__ F() : fx(), fy(), fz() {}
 
     __forceinline__ __device__
     const T operator() (const T x, const T y, const T z) const
     {
         return fx(x,y,z) * fy(x,y,z) * fz(x,y,z);
     }
 private:
     FX fx;
     FY fy;
     FZ fz;
 };

  
 template<typename T>
 class MG_Unit_Test_Curved_Ridges{
 
 public:
     typedef LaplaceOp<T> DiffOp;
 
     MG_Unit_Test_Curved_Ridges(){}
 
 
     class RHS{
     public:
         RHS(int n_points_per_dim,T h)
             :
             _n_points_per_dim(n_points_per_dim),
             _h(h)
         {}
 
         __forceinline__ __device__
         T operator () (const dim3 &grid_pos) const
         {
             Stencil stencil(_n_points_per_dim);
 
             stencil (grid_pos);
 
             int n_intervals_per_dim = _n_points_per_dim-1;
 
             bool boundary = (grid_pos.x == 0) || (grid_pos.x == n_intervals_per_dim)
                          || (grid_pos.y == 0) || (grid_pos.y == n_intervals_per_dim)
                          || (grid_pos.z == 0) || (grid_pos.z == n_intervals_per_dim);
 
             if (boundary)
                 return ref_sol(grid_pos);
             else
             return
                 / *partial with respect to x * /
                 5 * M_PI *(
                          10 * M_PI*(grid_pos.x*_h)
                          *(cos(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                          *(cos(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                          *(exp(2*sin(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                            - 8 * grid_pos.z * grid_pos.z )
                          +(exp(2*sin(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                            - 8 * grid_pos.z * grid_pos.z )
                          *(cos(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                          + 5 *M_PI*(grid_pos.*_h + 1)
                          *
                          (sin(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                         )
                 / *partial with respect to y * /
                 +
                 10 * M_PI*(grid_pos.*_h + 1)
                 *((10*M_PI*grid_pos.y*_h * grid_pos.y * _h)
                 *(cos(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                 *(cos(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h)))))
                 *(exp(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                 - 4 * grid_pos.z * grid_pos.z
                 +(exp(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                 - 4 * grid_pos.z * grid_pos.z
                 *(cos(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
                 -(5*M_PI*grid_pos.y*_h * 2*grid_pos.y * _h)
                 *(sin(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h))))
 
                 / *Partial wit respect to z* /
                 +
                 8 * (grid_pos.x*_h + 1)
                 *(8*(grid_pos.z*grid_pos.z) - 1)
                 *(exp(sin(5*M_PI*(grid_pos.x*_h + (grid_pos.y*_h)*(grid_pos.y*_h) ))
                 - 4 * grid_pos.z*_h *grid_pos.z *_h ));
 
 
 
         }
         __forceinline__ __device__
                 T
                 ref_sol(dim3 grid_pos) const
         {
             return (1 + grid_pos.x*_h)* exp(-4.0 * (grid_pos.z*_h * grid_pos.z*_h) + sin(5*M_PI*(grid_pos.x*_h + grid_pos.y*_h * grid_pos.y*_h)));
         }
     private:
         int _n_points_per_dim;
         T _h;
 
     };
 };
 
 
 template<typename T>
 class MG_Unit_Test_Gauss{
 
 public:
     typedef LaplaceOp<T> DiffOp;
 
 
     MG_Unit_Test_Gauss(){}
 
     class RHS{
     public:
         RHS(int n_points_per_dim,T h, T sigma)
             :
             _n_points_per_dim(n_points_per_dim),
             _h(h),
             _sigma2(sigma*sigma)
 
         {}
 
         __forceinline__ __device__
         T operator () (const dim3 &grid_pos) const
         {
             Stencil stencil(_n_points_per_dim);
 
             stencil (grid_pos);
 
             int n_intervals_per_dim = _n_points_per_dim-1;
 
             bool boundary = (grid_pos.x == 0) || (grid_pos.x == n_intervals_per_dim)
                          || (grid_pos.y == 0) || (grid_pos.y == n_intervals_per_dim)
                          || (grid_pos.z == 0) || (grid_pos.z == n_intervals_per_dim);
 
 
             if (boundary)
             {
                  return ref_sol(grid_pos);
             }
 
             else
             {
                 T x2 = grid_pos.x*_h * grid_pos.x*_h;
                 T y2 = grid_pos.y*_h * grid_pos.y*_h;
                 T z2 = grid_pos.z*_h * grid_pos.z*_h;
 
 
                 T f = exp(-16 *(x2 + y2 + z2));
 
 
 
                 return (-32 + 1024*x2) * f
                       +(-32 + 1024*y2) * f
                       +(-32 + 1024*z2) * f;
             }
 
 
 
 
         }
         __forceinline__ __device__
                 T
                 ref_sol(const dim3 grid_pos) const
         {
             return    exp(-16 *((grid_pos.x*_h * grid_pos.x*_h )
                              + (grid_pos.y*_h * grid_pos.y*_h )
                              + (grid_pos.z*_h * grid_pos.z*_h )
                              ));
 
 
         }
 
 
     private:
         int _n_points_per_dim;
         T _h;
         T _sigma2;
 
 
     };
 
 };

  
 __device__ int __red_black_ordering(int i, int j, int k){
 
     if( (i%2 == 0 && j%2==0 && k%2==0) || (i%2 == 1 && j%2==1 && k%2==0) ||
         (i%2 == 0 && j%2==1 && k%2==1) || (i%2 == 1 && j%2==0 && k%2==1))
         return 0;
 
     return 1;
 
 }

  
 __device__ bool _is_bound (dim3 grid_pos, int dim){
 
     if(grid_pos.x == 0 || grid_pos.x == dim-1 ||
        grid_pos.y == 0 || grid_pos.y == dim-1 ||
        grid_pos.z == 0 || grid_pos.z == dim-1)
     {
         return true;
     }
 
     return false;
 
 }

  
 template<typename T, typename DiffOp, typename RHS>
 __forceinline__ __device__
 void
 __sweep_test(T* phi, int i, int j, int n_intervals_per_dim, bool d,
         bool boundary_cond, DiffOp &laplace, const RHS &f){
 
     int color;
     int index;
 
     int dim_1 = n_intervals_per_dim + 1;
 
     if(d){
         index = 0;
     }else{
         index = 1;
     }
     dim3 grid_pos(i,j,0);
 
     Stencil stencil(dim_1);
 
     for(int k=1; k<dim_1-1; k++){
 
 
         grid_pos.z = k;
 
         color = __red_black_ordering(i,j,k);
 
         if(color == index)
         {
 
             if(!boundary_cond){
 
                 stencil(grid_pos);
                 phi[stencil.site] = stencil.site;
 
             }
          }
        __syncthreads();
     }
 }

  
 template<typename T, typename DiffOp, typename RHS>
 __forceinline__ __device__
 void
 __sweep(T* phi, int i, int j, int n_intervals_per_dim, bool d,
         bool boundary_cond, DiffOp &laplace, const RHS &f){
 
     int color;
     int index;
 
     int dim_1 = n_intervals_per_dim + 1;
 
     if(d){
         index = 0;
     }else{
         index = 1;
     }
     dim3 grid_pos(i,j,0);
 
     Stencil stencil(dim_1);
 
     for(int k=1; k<dim_1-1; k++){
 
 
         grid_pos.z = k;
 
         color = __red_black_ordering(i,j,k);
 
         if(color == index)
         {
 
             if(!boundary_cond){
 
                 stencil(grid_pos);
 
                 phi[stencil.site] -= (laplace(stencil, phi)-f(grid_pos))
                                      /
                                     laplace.grad_u(stencil, phi);
 
             }
          }
 
         __syncthreads();
     }
 }

  
 __device__ bool in_range(int i, int i_min, int i_sup)
 {
     return ((i >= i_min) && (i < i_sup));
 }

  
 __device__ bool __boundary_cond(int n_intervals_per_dim, int Halo_width, int i, int j){
 
     return !(in_range(i, Halo_width, n_intervals_per_dim + 1 - Halo_width)
          &&
             in_range(j, Halo_width, n_intervals_per_dim + 1 - Halo_width)
            );
 }

  
 template<typename T, typename DiffOp, typename RHS>
 __global__
 void __gauss_seidel(T* phi, int n_intervals_per_dim,
                     DiffOp laplace,
                     const RHS f)
 {
     int j = blockIdx.x * blockDim.x + threadIdx.x;
     int i = blockIdx.y * blockDim.y + threadIdx.y;
     bool cond;
     int Halo_width = 1;
 
     bool RED   = true;
     bool BLACK = false;
 
     if(i > (n_intervals_per_dim) && (j > n_intervals_per_dim) ) return;
 
     cond = __boundary_cond(n_intervals_per_dim, Halo_width, i , j);
 
     __sweep(phi, i, j, n_intervals_per_dim, RED, cond, laplace, f);
     __syncthreads();
 
     __sweep(phi, i, j, n_intervals_per_dim, BLACK, cond, laplace, f);
     __syncthreads();
 }

  
 template<typename T, typename TransferOp>
 __global__ void __grid_transfer(T* phi_H, T* phi_h, int n_intervals_per_dim,
                                 TransferOp transfer,bool prolongation)
 {
 
     int i = blockIdx.x * blockDim.x + threadIdx.x;
     int j = blockIdx.y * blockDim.y + threadIdx.y;
 
     int in_dim_1 = n_intervals_per_dim + 1;
 
     if (i >= in_dim_1) return;
     if (j >= in_dim_1) return;
 
     dim3 grid_pos(i,j,0);
 
     for(int k=0; k<in_dim_1; k++){
 
         grid_pos.z = k;
         / *printf("%d", site);* /
         if(prolongation)
         {
             transfer.prolongate(grid_pos, in_dim_1, phi_H, phi_h);
         }
         else
         {
             transfer.restriction(grid_pos, in_dim_1, phi_H, phi_h);
         }
 
         __syncthreads();
     }
 }
 
 
 #include "cuda_coarse_grid_cg.cu.c"

  
 template<typename T>
 void
 _gauss_seidel_unit_test(T* phi, int n_intervals_per_dim, T R, T h)
 {
 #if __CUDA_ARCH__ < 200
     int n_threads_per_block_dim = 16;
 #else
     int n_threads_per_block_dim = 32;
 #endif
     int blocks_per_dim = ((n_intervals_per_dim + 1)
                        +
                        n_threads_per_block_dim - 1)/n_threads_per_block_dim;
 
     int n_points_per_dim = (n_intervals_per_dim + 1);
     / *printf(" n block per dim %d \n",blocks_per_dim); * /
     dim3 grid(blocks_per_dim, blocks_per_dim);
     dim3 blocks(n_threads_per_block_dim,n_threads_per_block_dim);
     __gauss_seidel<<<grid,blocks>>>(phi,
                                     n_intervals_per_dim,
                                     typename MG_Unit_Test_Gauss<T>::DiffOp(),
                                     typename MG_Unit_Test_Gauss<T>::RHS(n_intervals_per_dim + 1,h, R)
     / *
                                     typename CGUnitTestProblem<T>::DiffOp(),
                                     typename CGUnitTestProblem<T>::RHS(n_points_per_dim)* /
                                     );
     cudaThreadSynchronize();
 }

  
 template<typename T>
 void
 _gauss_seidel(T* phi, int n_intervals_per_dim, T h, T sigma)
 {
 #if __CUDA_ARCH__ < 200
     int n_threads_per_block_dim = 16;
 #else
     int n_threads_per_block_dim = 32;
 #endif
     int blocks_per_dim = ((n_intervals_per_dim + 1)
                        +
                        n_threads_per_block_dim - 1)/n_threads_per_block_dim;
 
     / *printf(" n block per dim %d \n",blocks_per_dim);* /
     dim3 grid(blocks_per_dim, blocks_per_dim);
     dim3 blocks(n_threads_per_block_dim,n_threads_per_block_dim);
     __gauss_seidel<<<grid,blocks>>>(phi, n_intervals_per_dim,
                           typename MG_Unit_Test_Gauss<T>::DiffOp(),
                           typename MG_Unit_Test_Gauss<T>::RHS(n_intervals_per_dim + 1, h, sigma));
     cudaThreadSynchronize();
 }

  
 template<typename T>
 void
 _grid_transfer(T* phi_H, T* phi_h, int n_intervals_per_dim, bool prolongation)
 {
 #if __CUDA_ARCH__ < 200
     int n_threads_per_block_dim = 16;
 #else
     int n_threads_per_block_dim = 32;
 #endif
     int blocks_per_dim = ((n_intervals_per_dim+1)
                        +
                        n_threads_per_block_dim)/n_threads_per_block_dim;
 
     
     dim3 grid(blocks_per_dim, blocks_per_dim);
     
     dim3 blocks(n_threads_per_block_dim, n_threads_per_block_dim);
 
     __grid_transfer<<<grid,blocks>>>(phi_H, phi_h, n_intervals_per_dim,
                           InterGridOperator<T>(),prolongation);
 
     cudaThreadSynchronize();
 }
 
 
 void gauss_seidel(float* phi, int n_intervals_per_dim, float h, float sigma)
 {
     _gauss_seidel(phi, n_intervals_per_dim, h, sigma);
 }
 
 void gauss_seidel_unit_test(float* phi, int n_intervals_per_dim, float R, float h)
 {
     _gauss_seidel_unit_test(phi, n_intervals_per_dim, R, h);
 }
 
 void grid_transfer(float* phi_H, float * phi_h, int n_intervals_per_dim,
                     bool prolongation)
 {
     _grid_transfer(phi_H, phi_h,  n_intervals_per_dim, prolongation);
 }
 
 
 
 #ifndef USE_SINGLE_PRECISION
 void gauss_seidel(double* phi, int n_intervals_per_dim, double h, double sigma)
 {
     _gauss_seidel(phi, n_intervals_per_dim, h, sigma);
 }
 
 void gauss_seidel_unit_test(double* phi, int n_intervals_per_dim, double R, double h)
 {
     _gauss_seidel_unit_test(phi, n_intervals_per_dim, R, h);
 }
 
 void grid_transfer(double* phi_H, double * phi_h,
                    int n_intervals_per_dim, bool prolongation)
 {
     _grid_transfer(phi_H, phi_h,  n_intervals_per_dim, prolongation);
 }
 #endif

  
 template <typename T, typename F>
 __global__
 void
 __prolongation_unit_test( T * u_H, T * u_h, T* e_H, int n_intervals_per_dim, T h, int current_level)
 {
 
     int i = blockIdx.x * blockDim.x + threadIdx.x;
     int j = blockIdx.y * blockDim.y + threadIdx.y;
 
     int in_dim_1 = n_intervals_per_dim + 1;
 
     T tmp, tmp_e;
     dim3 grid_pos_h(i,j,0);
     dim3 grid_pos_H(i/2, j/2,0);
     T H = 2*h;
 
     if (i >= in_dim_1) return;
     if (j >= in_dim_1) return;
 
     Stencil s_h(in_dim_1);
     Stencil s_H(n_intervals_per_dim/2 + 1);
     const F f;
     InterGridOperator<T> transfer;
 
 
     for(int k=0; k<in_dim_1; k+=2){
 
         if( (grid_pos_h.x%2 == 0) && (grid_pos_h.y%2 == 0) )
         {
             grid_pos_H.z = k/2;
             s_H(grid_pos_H);
 
             tmp = f(H*grid_pos_H.x, H*grid_pos_H.y, H*grid_pos_H.z);
 
             if (current_level == 0)
                 u_H[s_H.site] = tmp;
 
             tmp_e = u_H[s_H.site] - tmp;
             / *e_H[s_H.site] =  u_H[s_H.site];* /
             e_H[s_H.site] = tmp_e * tmp_e;
             / * u_H[s_H.site] = tmp;* /
         }        
     }
 __syncthreads();
 
 
     for(int k=0; k<in_dim_1; k++){
 
         grid_pos_h.z = k;
 
         transfer.prolongate(grid_pos_h, in_dim_1, u_H, u_h);
 
         if (is_boundary_point(grid_pos_h, in_dim_1))
         {
             s_h(grid_pos_h);
             tmp = f(h*grid_pos_h.x, h*grid_pos_h.y, h*grid_pos_h.z);
             u_h[s_h.site] = tmp;
         }
 
         __syncthreads();
     }
 
 }

  
 template<typename T>
 void
 _prolongation_unit_test( T * u_H, T * u_h, T* e_H,
                          int n_intervals_per_dim, T h, int current_level,
                          Selectors::TransferTestfunction ftest)
 {
 
 #if __CUDA_ARCH__ < 200
     int n_threads_per_block_dim = 16;
 #else
     int n_threads_per_block_dim = 16;
 #endif
     int blocks_per_dim = ((n_intervals_per_dim)
                        +
                        n_threads_per_block_dim)/n_threads_per_block_dim;
 
     dim3 grid(blocks_per_dim, blocks_per_dim);
 
     dim3 blocks(n_threads_per_block_dim, n_threads_per_block_dim);
 
 
     typedef Constant<T> one;
 
     typedef F< X<T>,        Constant<T>, Constant<T> > x;
     typedef F< Constant<T>, Y<T>,        Constant<T> > y;
     typedef F< Constant<T>, Constant<T>, Z<T>        > z;
 
     typedef F< x, y, one > xy;
     typedef F< x, one, z > xz;
     typedef F< one, y, z > yz;
     typedef F< x, y, z > xyz;
 
     typedef F< x, x, one > xx;
     typedef F< y, y, one > yy;
     typedef F< one, z, z > zz;
 
     typedef F< z, z, z > zzz;
 
     typedef F< xx, yy, one > xxyy;
     typedef F< xx, yy, z > xxyz;
     typedef F< one,Y<T>, Y<T> > yyzz;
     typedef F< x, yy, z> xyyz;
     typedef F< x,y , zz> xyzz;
 
     typedef F< x, y, zzz > xyzzz;
 
 
 
     switch (ftest) {
     case Selectors::one:
          __prolongation_unit_test<T,one><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::x:
          __prolongation_unit_test<T,x><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::y:
          __prolongation_unit_test<T,y><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::z:
          __prolongation_unit_test<T,z><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xy:
          __prolongation_unit_test<T,xy><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xz:
          __prolongation_unit_test<T,xz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::yz:
          __prolongation_unit_test<T,yz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyz:
          __prolongation_unit_test<T,xyz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xx:
          __prolongation_unit_test<T,xx><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::yy:
          __prolongation_unit_test<T,yy><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::zz:
          __prolongation_unit_test<T,zz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xxyy:
          __prolongation_unit_test<T,xxyy><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xxyz:
          __prolongation_unit_test<T,xxyz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::yyzz:
          __prolongation_unit_test<T,yyzz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyyz:
          __prolongation_unit_test<T,xyyz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyzz:
          __prolongation_unit_test<T,xyzz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyzzz:
          __prolongation_unit_test<T,xyzzz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
 
     default:
          break;
     }
 
     cudaThreadSynchronize();
 }
 
 
 void prolongation_unit_test( double * u_H, double * u_h, double* e_H,
                              int n_intervals_per_dim, double h, int current_level, Selectors::TransferTestfunction ftest)
 {
     _prolongation_unit_test(u_H, u_h, e_H, n_intervals_per_dim, h, current_level, ftest);
 }

  
 template <typename T, typename F>
 __global__
 void
 __restriction_unit_test( T * u_H, T * u_h, T* e_H, int n_intervals_per_dim, T h, int current_level)
 {
 
     int i = blockIdx.x * blockDim.x + threadIdx.x;
     int j = blockIdx.y * blockDim.y + threadIdx.y;
 
     int in_dim_1 = n_intervals_per_dim + 1;
 
     T tmp, tmp_e;
     dim3 grid_pos_h(i,j,0);
     dim3 grid_pos_H(i/2, j/2,0);
     T H = 2*h;
 
     if (i >= in_dim_1) return;
     if (j >= in_dim_1) return;
 
     Stencil s_h(in_dim_1);
     Stencil s_H((n_intervals_per_dim/2) + 1);
     const F f;
     InterGridOperator<T> transfer;
 
 
 
     if (current_level == 0){
 
         for(int k=0; k<in_dim_1; k++){
 
             s_h(grid_pos_h);
             tmp = f(h*grid_pos_h.x, h*grid_pos_h.y, h*grid_pos_h.z);
             u_h[s_h.site] = tmp;
 
         }
 
     }
 
 
 
     for(int k=0; k<in_dim_1; k++){
 
         grid_pos_h.z = k;
 
         transfer.restriction(grid_pos_h, in_dim_1, u_H, u_h);
 
         if (is_boundary_point(grid_pos_h, in_dim_1))
         {
             s_h(grid_pos_h);
             tmp = f(h*grid_pos_h.x, h*grid_pos_h.y, h*grid_pos_h.z);
             u_h[s_h.site] = tmp;
         }
 
         __syncthreads();
     }
 
     for(int k=0; k<in_dim_1; k+=2){
 
         if( (grid_pos_h.x%2 == 0) && (grid_pos_h.y%2 == 0) )
         {
             grid_pos_H.z = k/2;
             s_H(grid_pos_H);
 
             tmp = f(H*grid_pos_H.x, H*grid_pos_H.y, H*grid_pos_H.z);
 
             tmp_e = u_H[s_H.site] - tmp;
             / *e_H[s_H.site] =  u_H[s_H.site];* /
             e_H[s_H.site] = tmp_e * tmp_e;
            / * u_H[s_H.site] = tmp;* /
         }
     }
 
 }

  
 template<typename T>
 void
 _restriction_unit_test( T * u_H, T * u_h, T* e_H,
                         int n_intervals_per_dim, T h, int current_level,
                         Selectors::TransferTestfunction ftest)
 {
 
 #if __CUDA_ARCH__ < 200
     int n_threads_per_block_dim = 16;
 #else
     int n_threads_per_block_dim = 16;
 #endif
     int blocks_per_dim = ((n_intervals_per_dim)+n_threads_per_block_dim)/n_threads_per_block_dim;
 
     dim3 grid(blocks_per_dim, blocks_per_dim);
 
     dim3 blocks(n_threads_per_block_dim, n_threads_per_block_dim);
 
     typedef Constant<T> one;
 
     typedef F< X<T>,        Constant<T>, Constant<T> > x;
     typedef F< Constant<T>, Y<T>,        Constant<T> > y;
     typedef F< Constant<T>, Constant<T>, Z<T>        > z;
 
     typedef F< x, y, one > xy;
     typedef F< x, one, z > xz;
     typedef F< one, y, z > yz;
     typedef F< x, y, z > xyz;
     typedef F< x, x, one > xx;
     typedef F< y, y, one > yy;
     typedef F< one, z, z > zz;
 
     typedef F< z, z, z > zzz;
 
 
     typedef F< xx, yy, one > xxyy;
     typedef F< xx, yy, z > xxyz;
     typedef F< one,Y<T>, Y<T> > yyzz;
     typedef F< x, yy, z> xyyz;
     typedef F< x,y , zz> xyzz;
 
     typedef F< x, y, zzz > xyzzz;
 
 
     switch (ftest) {
     case Selectors::one:
          __restriction_unit_test<T,one><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::x:
          __restriction_unit_test<T,x><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::y:
          __restriction_unit_test<T,y><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::z:
          __restriction_unit_test<T,z><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xy:
          __restriction_unit_test<T,xy><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xz:
          __restriction_unit_test<T,xz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::yz:
          __restriction_unit_test<T,yz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyz:
          __restriction_unit_test<T,xyz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xx:
          __restriction_unit_test<T,xx><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::yy:
          __restriction_unit_test<T,yy><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::zz:
          __restriction_unit_test<T,zz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xxyy:
          __restriction_unit_test<T,xxyy><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xxyz:
          __restriction_unit_test<T,xxyz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::yyzz:
          __restriction_unit_test<T,yyzz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyyz:
          __restriction_unit_test<T,xyyz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyzz:
          __restriction_unit_test<T,xyzz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
     case Selectors::xyzzz:
          __restriction_unit_test<T,xyzzz><<<grid,blocks>>>(u_H, u_h, e_H, n_intervals_per_dim, h, current_level);
          break;
 
     default:
          break;
     }
 
     cudaThreadSynchronize();
 }
 
 
 void restriction_unit_test( double * u_H, double * u_h, double* e_H,
                             int n_intervals_per_dim, double h, int current_level,
                             Selectors::TransferTestfunction ftest)
 {
     _restriction_unit_test(u_H, u_h, e_H,
                            n_intervals_per_dim, h,
                            current_level, ftest);
 }

  
 template<typename T, typename DiffOp, typename RHS>
 __global__
 void __MG_reference_solution(T* e_h, T* u_h, int n_intervals_per_dim,
                             DiffOp laplace,
                             const RHS f, bool reference_or_error)
 {
     int j = blockIdx.x * blockDim.x + threadIdx.x;
     int i = blockIdx.y * blockDim.y + threadIdx.y;
 
     if (i > n_intervals_per_dim) return;
     if (j > n_intervals_per_dim) return;
 
     int dim_1 = n_intervals_per_dim + 1;
 
     dim3 grid_pos(i,j,0);
 
     Stencil stencil(dim_1);
 
 
     for(int k=0; k<dim_1; k++){
 
         grid_pos.z = k;
 
         stencil(grid_pos);
 
         if( _is_bound (grid_pos,  n_intervals_per_dim))
         {
             u_h[stencil.site] = f.ref_sol(grid_pos);
         }
 
         if(reference_or_error) // reference
         {
             e_h[stencil.site] = f.ref_sol(grid_pos);
         }
         else //or error
         {
             e_h[stencil.site] = f.ref_sol(grid_pos);
             e_h[stencil.site] -= u_h[stencil.site];
         }
 
     }
 }

  
 template<typename T>
 void
 _MG_reference_solution(T* e_h, T* u_h, int n_intervals_per_dim, T h, T sigma, bool reference_or_error)
 {
 #if __CUDA_ARCH__ < 200
     int n_threads_per_block_dim = 16;
 #else
     int n_threads_per_block_dim = 32;
 #endif
     int blocks_per_dim = ((n_intervals_per_dim + 1)
                        +
                        n_threads_per_block_dim - 1)/n_threads_per_block_dim;
 
     / *printf(" n block per dim %d \n",blocks_per_dim);* /
     dim3 grid(blocks_per_dim, blocks_per_dim);
     dim3 blocks(n_threads_per_block_dim,n_threads_per_block_dim);
     __MG_reference_solution<<<grid,blocks>>>(e_h,u_h,n_intervals_per_dim,
                                     typename MG_Unit_Test_Gauss<T>::DiffOp(),
                                     typename MG_Unit_Test_Gauss<T>::RHS((n_intervals_per_dim + 1), h, sigma),
                                     reference_or_error);
     cudaThreadSynchronize();
 }
 
 
 
 
 
 
 void MG_reference_solution(float* e_h, float* u_h, int n_intervals_per_dim, float h, float sigma, bool reference_or_error)
 {
     _MG_reference_solution(e_h, u_h, n_intervals_per_dim, h, sigma, reference_or_error);
 }
 
 #ifndef USE_SINGLE_PRECISION
 void MG_reference_solution(double* e_h, double* u_h, int n_intervals_per_dim, double h, double sigma, bool reference_or_error)
 {
     _MG_reference_solution(e_h, u_h, n_intervals_per_dim, h, sigma, reference_or_error);
 }
 #endif
 
 
 
 
 
 #ifndef CUDADriver_STEP_12_H
 #define CUDADriver_STEP_12_H
 
 #include <lac/blas++.h>
 #include <base/parameter_handler.h>
 #include <cuda_kernel_wrapper_step-12.cu.h>
 
 
 namespace step12 {

  
     struct SimParam {
 
         static void declare(::ParameterHandler & prm);
         void get(::ParameterHandler & prm);
         void run(std::string prm_filename);
 
         int max_level;
         bool disp_mem_consumption, disp_phi_max_size, disp_error_matrix,
              disp_transfer_dimension_resize_info, disp_transfer_error, disp_data_matrix,
              disp_transfer_time, disp_pointer, disp_current_level;
 
         std::string n_cycle;
 
         QString test_functions;
 
         std::vector<Selectors::TransferTestfunction> tests;
         std::map<QString, Selectors::TransferTestfunction> prm_name2enum,
                                                            transfer_tests;
 
         SimParam(){
             prm_name2enum["one"]=Selectors::one;
             prm_name2enum["x"]=Selectors::x;
             prm_name2enum["y"]=Selectors::y;
             prm_name2enum["z"]=Selectors::z;
             prm_name2enum["xy"]=Selectors::xy;
             prm_name2enum["xz"]=Selectors::xz;
             prm_name2enum["yz"]=Selectors::yz;
             prm_name2enum["xyz"]=Selectors::xyz;
             prm_name2enum["xx"]=Selectors::xx;
             prm_name2enum["yy"]=Selectors::yy;
             prm_name2enum["zz"]=Selectors::zz;
             prm_name2enum["xxyy"]=Selectors::xxyy;
             prm_name2enum["xxyz"]=Selectors::xxyz;
             prm_name2enum["yyzz"]=Selectors::yyzz;
             prm_name2enum["xyyz"]=Selectors::xyyz;
             prm_name2enum["xyzz"]=Selectors::xyzz;
             prm_name2enum["xyzzz"]=Selectors::xyzzz;
 
         }
 
     };

  
     void
     SimParam::declare(::ParameterHandler &prm)
     {
         prm.enter_subsection("Choose unit test");
 
         prm.declare_entry("Max level", "1",
                           ::Patterns::Integer(),
                           "Maximum level of multigrid cycles.\n"
                           "  # Possible values : 1,2,3...");
         prm.declare_entry("Type of cycle", "v",
                           ::Patterns::Anything(),
                           "Type of Cycle(v,w). "
                           "Multigrid cycles types defined in Wesseling"
                           "  # Possible values: v,w");
 
         prm.declare_entry("Display memory consumption", "false",
                           ::Patterns::Bool(),
                           "Displaying memory consumption of all solutions"
                           "");
 
         prm.declare_entry("Display finest grid size", "false",
                           ::Patterns::Bool(),
                           "Displaying grid size of the maximum level"
                           "");
 
 
 
 
         mg_unit_test.test_Multigrid();
 
 
         prm.leave_subsection();
 
         prm.enter_subsection("Grid transfer tests");
 
         prm.declare_entry("Test functions", "one, x, y, z",
                           ::Patterns::Anything(),
                           "Functions for testing the multigrid transfer. "
                           "Transfer is done via multilinear interpolation."
                           "Test functions comprise the set of functions "
                           "that can be transferred exactly (all multilinear"
                           "combinations of one, x,y,z)"
                           "and several which are quadratic or cubic in one component"
                           "in order to reproduce"
                           "interpolation errors."
                           "Possible values : one, x, y, z, xy, xz, yz, xyz, xx, yy, zz, xxyy, xxyz, "
                           "yyzz, xyyz, xyzz, xyzzz");
 
         prm.declare_entry("Max level", "1",
                           ::Patterns::Integer(),
                           "Maximum level of multigrid cycles.\n"
                           "  # Possible values : 1,2,3...");
         prm.declare_entry("Type of cycle", "v",
                           ::Patterns::Anything(),
                           "Type of Cycle(v,w). "
                           "Multigrid cycles types defined in Wesseling"
                           "  # Possible values: v,w");
 
         prm.declare_entry("Display memory consumption", "false",
                           ::Patterns::Bool(),
                           "Displaying memory consumption of all solutions"
                           "");
 
         prm.declare_entry("Display finest grid size", "false",
                           ::Patterns::Bool(),
                           "Displaying grid size of the maximum level"
                           "");
         prm.declare_entry("Display error matrix", "false",
                           ::Patterns::Bool(),
                           "Displaying error matrix of one resizing step"
                           "");
         prm.declare_entry("Display dimension information", "false",
                           ::Patterns::Bool(),
                           "Displaying dimensions of the current reference solution "
                           "matrix "
                           "");
         prm.declare_entry("Display transfer error", "false",
                           ::Patterns::Bool(),
                           "Displaying l2 norm of the error vector of one resizing step."
                           "");
         prm.declare_entry("Display reference solution", "false",
                           ::Patterns::Bool(),
                           "Displaying current reference solution matrix "
                           "containing actual data "
                           "");
         prm.declare_entry("Display transfer time", "false",
                           ::Patterns::Bool(),
                           "Displaying transfer time between two levels"
                           "");
         prm.declare_entry("Display pointers", "false",
                           ::Patterns::Bool(),
                           "Displaying begin of the areas within the whole "
                           "refernce solution vector"
                           "");
         prm.declare_entry("Display current level", "false",
                           ::Patterns::Bool(),
                           "Displaying level of a current multigrid cycle, "
                           "0 at the bottom"
                           "");
 
         prm.leave_subsection();
 
         prm.enter_subsection("Grid transfer tests");
 
         prm.leave_subsection();
     }

  
     void
     SimParam::get(::ParameterHandler &prm)
     {
         prm.enter_subsection("Grid transfer tests");
 
         test_functions = QString(prm.get("Test functions").c_str());
         max_level = prm.get_integer("Max level");
         n_cycle = prm.get("Type of cycle");
         disp_mem_consumption = prm.get_bool("Display memory consumption");
         disp_phi_max_size = prm.get_bool("Display finest grid size");
         disp_error_matrix = prm.get_bool("Display error matrix");
         disp_transfer_dimension_resize_info = prm.get_bool("Display dimension information");
         disp_transfer_error = prm.get_bool("Display transfer error");
 
         disp_data_matrix = prm.get_bool("Display reference solution");
         disp_transfer_time = prm.get_bool("Display transfer time");
         disp_pointer = prm.get_bool("Display pointers");
         disp_current_level = prm.get_bool("Display current level");
 
         prm.leave_subsection();
 
         QStringList tmp = test_functions.split(",", QString::SkipEmptyParts);
         QStringList::const_iterator e = tmp.begin(),ende = tmp.end();
 
         for(; e!=ende;++e)
         {
             std::map<QString, Selectors::TransferTestfunction>
             ::
             const_iterator result = prm_name2enum.find(*e);
 
             if( result!= prm_name2enum.end() )
                 transfer_tests[result->first] = result->second;
 
         }
 
         if (!tmp.empty() && transfer_tests.empty())
             std::cerr << "WARNING : NO VALID TEST FUNCTIONS FOR GRID TRANSFER TESTS SELECTED!!! "<<
                          "CHECK prm file." << std::endl;
 
     }

  
 template<typename T>
 class CUDAUnitTestDriver {
 
     const SimParam * __params;
 
     public:
 
         typedef typename blas_pp<T,cublas>::Vector Vector;
 
         CUDAUnitTestDriver(const SimParam &p)
             :
             __params(&p)
         {
             Vector::blas_wrapper_type::Init();
             cudaThreadSynchronize();
         }
 
     ~CUDAUnitTestDriver() { Vector::blas_wrapper_type::Shutdown(); }
 
 
     void test_coarse_CG_solver();
 
     void test_gauss_seidel();
 
     void test_grid_transfer();
 
     void test_grid_transfer_implementation(Selectors::TransferTestfunction test_function);
 
     void test_Multigrid();

  
     class Potential : public Vector {
 
         typedef typename Vector::blas_wrapper_type BW;
 
         public:
 
             typedef Vector Base;
 
             Potential() : Vector() {}
             Potential(int n_elements) : Vector(n_elements) {}

  
             void
             print(std::ostream &out) const
             {
                 std::vector<T> tmp(this->__n);
                 T * dst_ptr = &tmp[0];
 
                 const T * src_ptr = this->val();
 
                 BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
                 int dim_x, dim_y;
                 dim_x = pow(this->__n, 1/3.);
 
                 while (dim_x*dim_x*dim_x > this->__n)
                     if (dim_x*dim_x*dim_x > this->__n)
                     --dim_x;
 
                 while (dim_x*dim_x*dim_x < this->__n)
                     if (dim_x*dim_x*dim_x < this->__n)
                         ++dim_x;
 
                 dim_y = dim_x * dim_x;
 
 
                Assert((dim_x*dim_x*dim_x) == this->__n,
                       ::ExcMessage("Bummer"));
 
 
                 for (int i = 0; i < this->__n; i=i+dim_y){
                     out<<std::endl;
                     for (int j = i; j<dim_y+i ; j+=dim_x){
                         out<<std::endl;
 
                         for (int k = j; k<dim_x+j; ++k){
 
                             out<< std::fixed
                              << std::setprecision(3) << tmp[k]<<"  ";
                         }
                     }
                 }
                 out<<std::endl;
                 out<<std::endl;
             }

  
             void
             print_gnu_plot(std::ostream &out) const
             {
                 std::vector<T> tmp(this->__n);
                 T * dst_ptr = &tmp[0];
 
                 const T * src_ptr = this->val();
 
                 BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
                 T dim_x, dim_2;
                 dim_x = pow(this->__n,1/3.);
                 / *dim_x++;* /
                 dim_2 = pow(dim_x,2);
 
                 / * for (int i = 0; i < this->__n; i++){
                    out<<tmp[i]<<"\n";
                 }* /
 
                dim_x = (int)dim_x+1;
                dim_2 = (int)dim_2+1;
                out<< "#" << dim_x<<std::endl;
                out<< "#" << dim_2<<std::endl;
                out<< "#" << this->__n<<std::endl;
 
                 for (int i = 0; i < this->__n; i=i+dim_2){
                     out<<std::endl;
                     for (int j = i; j<dim_2+i ; j+=dim_x){
                         out<<std::endl;
 
                         for (int k = j; k<dim_x+j; ++k){
 
                             out<< std::fixed << std::setprecision(6) << tmp[k]<<"\n";
 
                             / *if((k-(int)dim_x-1)%(int)dim_2 == 0){
                                out<<tmp[k]<<" ";
                              }
                             out<<tmp[k]<<" ";* /
 
                         }
                     }
                 }
                 out<<std::endl;
                 out<<std::endl;
             }

  
             void
             print_transfer(std::ostream &out, int mesh, int max_level) const
             {
                 std::vector<T> tmp(this->__n);
                 T * dst_ptr = &tmp[0];
 
                 const T * src_ptr = this->val();
 
                 BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
                 int dim_y, dim_z;
                 int sum;
                 int dim_x = mesh;
                 int start = 0;
                 for(int l = 0; l<max_level+1; l++)
                 {
                     if(l==0)
                         dim_x = dim_x;
                     else
                         dim_x =((dim_x-1)*2)+1;
 
                     dim_y = dim_x * dim_x;
                     dim_z = dim_x * dim_x * dim_x;
                     out<< "whole : " << this->__n<<std::endl;
 
                     out<< "dim x : " << dim_x<<std::endl;
                     out<< "dim x * dim y : " << dim_y<<std::endl;
                     out<< "dim x * dim y * dim z : " << dim_z<<std::endl;
 
                     / *Assert((dim_x*dim_x*dim_x) == this->__n,
                            ::ExcMessage("Bummer"));* /
 
 
 
                      out<<std::endl;
                      out<<std::endl;
 
                     for (int i = start; i<dim_z+start; i=i+dim_y){
 
                         out<<std::endl;
                         for (int j = i; j<dim_y+i ; j+=dim_x){
                             out<<std::endl;
 
                             for (int k = j; k<dim_x+j; ++k){
 
                                 out<< std::fixed
                                  << std::setprecision(3) << tmp[k]<<"  ";
                             }
 
 
                         }
                     }
                     out<<std::endl;
                     / *start* /
                     start += dim_z;
 
 
                 }
             }

  
             void
             print_multigrid_gnu(std::ostream &out, int mesh, int max_level) const
             {
                 std::vector<T> tmp(this->__n);
                 T * dst_ptr = &tmp[0];
 
                 const T * src_ptr = this->val();
 
                 BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
                 int dim_y, dim_z;
 
                 int dim_x = mesh;
                 int start = 0;
                 for(int l = 0; l<=max_level; l++)
                 {
                     if(l==0)
                         dim_x = dim_x;
                     else
                         dim_x =((dim_x-1)*2)+1;
 
                     dim_y = dim_x * dim_x;
                     dim_z = dim_x * dim_x * dim_x;
                     out<< "#whole : " << this->__n<<std::endl;
 
                     out<< "#dim x : " << dim_x<<std::endl;
                     out<< "#dim x * dim y : " << dim_y<<std::endl;
                     out<< "#dim x * dim y * dim z : " << dim_z<<std::endl;
 
                     / *Assert((dim_x*dim_x*dim_x) == this->__n,
                            ::ExcMessage("Bummer"));* /
 
 
                      out<<std::endl;
                      out<<std::endl;
 
                     for (int i = start; i<dim_z+start; i=i+dim_y){
                         out<<std::endl;
                         for (int j = i; j<dim_y+i ; j+=dim_x){
                             out<<std::endl;
 
                             for (int k = j; k<dim_x+j; ++k){
                                 if(l == max_level)
                                     out<< std::fixed
                                         << std::setprecision(6) << tmp[k]<<"\n";
                             }
                         }
                     }
                     out<<std::endl;
                     start += dim_z;
 
 
                 }
             }
 
 
 
         private:
 
             Potential(const Potential& / *other* /) {}
 
             Potential & operator = (const Potential& / *other* /) {}
         };
 
 
 private:
 
     Potential phi;
     Potential e_H;
 
 };

  
 template<typename T>
 class CUDADriver {
 
     const SimParam * __params;
 
 public:
 
     typedef typename blas_pp<T,cublas>::Vector Vector;
 
     CUDADriver(const SimParam &p)
         :
         __params(&p)
     {
         Vector::blas_wrapper_type::Init();
         cudaThreadSynchronize();
     }
 
     ~CUDADriver() { Vector::blas_wrapper_type::Shutdown(); }
 
 
     void coarse_CG_solver();

  
     class Potential : public Vector {
 
         typedef typename Vector::blas_wrapper_type BW;
 
     public:
 
         typedef Vector Base;
 
         Potential() : Vector() {}
         Potential(int n_elements) : Vector(n_elements) {}

  
         void
                 print(std::ostream &out) const
         {
             std::vector<T> tmp(this->__n);
             T * dst_ptr = &tmp[0];
 
             const T * src_ptr = this->val();
 
             BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
             int dim_x, dim_y;
             dim_x = pow(this->__n, 1/3.);
 
             while (dim_x*dim_x*dim_x > this->__n)
                 if (dim_x*dim_x*dim_x > this->__n)
                     --dim_x;
 
             while (dim_x*dim_x*dim_x < this->__n)
                 if (dim_x*dim_x*dim_x < this->__n)
                     ++dim_x;
 
             dim_y = dim_x * dim_x;
 
 
             Assert((dim_x*dim_x*dim_x) == this->__n,
                    ::ExcMessage("Bummer"));
 
 
             for (int i = 0; i < this->__n; i=i+dim_y){
                 out<<std::endl;
                 for (int j = i; j<dim_y+i ; j+=dim_x){
                     out<<std::endl;
 
                     for (int k = j; k<dim_x+j; ++k){
 
                         out<< std::fixed
                                 << std::setprecision(3) << tmp[k]<<"  ";
                     }
                 }
             }
             out<<std::endl;
             out<<std::endl;
         }

  
         void
                 print_gnu_plot(std::ostream &out) const
         {
             std::vector<T> tmp(this->__n);
             T * dst_ptr = &tmp[0];
 
             const T * src_ptr = this->val();
 
             BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
             T dim_x, dim_2;
             dim_x = pow(this->__n,1/3.);
             / *dim_x++;* /
             dim_2 = pow(dim_x,2);
 
             / * for (int i = 0; i < this->__n; i++){
                out<<tmp[i]<<"\n";
             }* /
 
             dim_x = (int)dim_x+1;
             dim_2 = (int)dim_2+1;
             out<< "#" << dim_x<<std::endl;
             out<< "#" << dim_2<<std::endl;
             out<< "#" << this->__n<<std::endl;
 
             for (int i = 0; i < this->__n; i=i+dim_2){
                 out<<std::endl;
                 for (int j = i; j<dim_2+i ; j+=dim_x){
                     out<<std::endl;
 
                     for (int k = j; k<dim_x+j; ++k){
 
                         out<< std::fixed << std::setprecision(6) << tmp[k]<<"\n";
 
                         / *if((k-(int)dim_x-1)%(int)dim_2 == 0){
                            out<<tmp[k]<<" ";
                          }
                         out<<tmp[k]<<" ";* /
 
                     }
                 }
             }
             out<<std::endl;
             out<<std::endl;
         }

  
         void
                 print_transfer(std::ostream &out, int mesh, int max_level) const
         {
             std::vector<T> tmp(this->__n);
             T * dst_ptr = &tmp[0];
 
             const T * src_ptr = this->val();
 
             BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
             int dim_y, dim_z;
             int sum;
             int dim_x = mesh;
             int start = 0;
             for(int l = 0; l<max_level+1; l++)
             {
                 if(l==0)
                     dim_x = dim_x;
                 else
                     dim_x =((dim_x-1)*2)+1;
 
                 dim_y = dim_x * dim_x;
                 dim_z = dim_x * dim_x * dim_x;
                 out<< "whole : " << this->__n<<std::endl;
 
                 out<< "dim x : " << dim_x<<std::endl;
                 out<< "dim x * dim y : " << dim_y<<std::endl;
                 out<< "dim x * dim y * dim z : " << dim_z<<std::endl;
 
                 / *Assert((dim_x*dim_x*dim_x) == this->__n,
                        ::ExcMessage("Bummer"));* /
 
 
 
                 out<<std::endl;
                 out<<std::endl;
 
                 for (int i = start; i<dim_z+start; i=i+dim_y){
 
                     out<<std::endl;
                     for (int j = i; j<dim_y+i ; j+=dim_x){
                         out<<std::endl;
 
                         for (int k = j; k<dim_x+j; ++k){
 
                             out<< std::fixed
                                     << std::setprecision(3) << tmp[k]<<"  ";
                         }
 
 
                     }
                 }
                 out<<std::endl;
                 / *start* /
                 start += dim_z;
 
 
             }
         }

  
         void
                 print_multigrid_gnu(std::ostream &out, int mesh, int max_level) const
         {
             std::vector<T> tmp(this->__n);
             T * dst_ptr = &tmp[0];
 
             const T * src_ptr = this->val();
 
             BW::GetVector(this->__n, src_ptr, 1, dst_ptr, 1);
 
             int dim_y, dim_z;
 
             int dim_x = mesh;
             int start = 0;
             for(int l = 0; l<=max_level; l++)
             {
                 if(l==0)
                     dim_x = dim_x;
                 else
                     dim_x =((dim_x-1)*2)+1;
 
                 dim_y = dim_x * dim_x;
                 dim_z = dim_x * dim_x * dim_x;
                 out<< "#whole : " << this->__n<<std::endl;
 
                 out<< "#dim x : " << dim_x<<std::endl;
                 out<< "#dim x * dim y : " << dim_y<<std::endl;
                 out<< "#dim x * dim y * dim z : " << dim_z<<std::endl;
 
                 / *Assert((dim_x*dim_x*dim_x) == this->__n,
                        ::ExcMessage("Bummer"));* /
 
 
                 out<<std::endl;
                 out<<std::endl;
 
                 for (int i = start; i<dim_z+start; i=i+dim_y){
                     out<<std::endl;
                     for (int j = i; j<dim_y+i ; j+=dim_x){
                         out<<std::endl;
 
                         for (int k = j; k<dim_x+j; ++k){
                             if(l == max_level)
                                 out<< std::fixed
                                         << std::setprecision(6) << tmp[k]<<"\n";
                         }
                     }
                 }
                 out<<std::endl;
                 start += dim_z;
 
 
             }
         }
 
 
 
     private:
 
         Potential(const Potential& / *other* /) {}
 
         Potential & operator = (const Potential& / *other* /) {}
     };
 
 
 private:
 
     Potential phi;
     Potential e_H;
 
 };
 
 } // namespace step12 END
 
 #endif // CUDADriver_STEP_12_H
 
 
 
 #ifndef CUDA_DRIVER_STEP_12_HH
 #define CUDA_DRIVER_STEP_12_HH
 #include "cuda_driver_step-12.h"
 #include <fstream>
 
 #include <QString>
 
 #include <base/timer.h>
 
 #include <base/CUDATimer.h>
 #include <base/convergence_table.h>
 
 #include "cuda_kernel_wrapper_step-12.cu.h"
 #include <cutil_inline.h>

  
 template<typename T>
 void step12::CUDAUnitTestDriver<T>::test_coarse_CG_solver()
 {
     int n_intervals_per_dim = MESH_DIM-1;
     int n_points_per_dim = n_intervals_per_dim+1;
     int n_points = n_points_per_dim * n_points_per_dim * n_points_per_dim;
 
     Potential reference_solution;
 
 
 
     ::ConvergenceTable convergence_history;
 
     for (int iter = 1; iter < coarse_cg_max_iter; iter++)
     {
         phi.reinit(n_points);
 
         {
             std::vector<T> tmp(n_points);
 
             for (int k = 0; k < n_points; k++)
                 tmp[k] = 1 + std::sin(k);
 
             typename Potential::Base & rs_ref = reference_solution;
             rs_ref = tmp;
 
 
             int x, y, z;
 
             for (int i = 0; i < n_points; i++)
             {
                 x = i%n_points_per_dim;
                 y = (i%(n_points_per_dim*n_points_per_dim))/n_points_per_dim;
                 z = i/(n_points_per_dim * n_points_per_dim);
 
                 bool boundary =    (x == 0) || (x == n_intervals_per_dim)
                                    || (y == 0) || (y == n_intervals_per_dim)
                                    || (z == 0) || (z == n_intervals_per_dim);
 
                 if (!boundary)
                     tmp[i] = 0;
             }
 
 
             typename Potential::Base & ref = phi;
             ref = tmp;
 
             phi.print(std::cout);
         }
 
         if(print_sols){
         std::cout
                 << "||Phi_ref||_2 : " << reference_solution.l2_norm()
                 << std::endl;
         }
         if(print_sols) {
             std::cout
                     << "Phi_ref : " << std::endl;
             reference_solution.print(std::cout);
         }
 
         if(print_sols){
         std::cout
                 << "||Phi_0||_2 : " << phi.l2_norm()
                 << std::endl;
         std::cout << "Phi_0: \n\n";
         }
 
         if(print_sols)
             phi.print(std::cout);
 
         T tolerance = cg_tol;
         typename Potential::Base residual(7*coarse_cg_max_iter+2);
         {
             std::vector<T> tmp(residual.size(), 0.);
             residual = tmp;
         }
 
 
         CUDATimer cg_timer;
         coarse_grid_CG_solve_unit_test(phi.array().val(),
                                        n_points_per_dim,
                                        tolerance,
                                        iter,
                                        residual.array().val());
 
         if(print_sols)
             cg_timer.print_elapsed("Time spent in coarse grid solve : ");
 
         if(print_sols)
             std::cout<<  "||Phi_final||_2 : " << phi.l2_norm()<<std::endl;
 
         if(print_sols){
         std::cout
                 << "N Threads : " << N_COARSE_GRID_THREADS
                 << ", N elements : " << phi.size()
                 << ", Residuals: \n\n" << std::setprecision(10);
 
 
         std::cout << "Phi: \n\n";
         }
 
         if(print_sols)
             phi.print(std::cout);
 
 
 
         phi -= reference_solution;
 
         if(print_sols)
             std::cout << "Phi_final - Phi_ref: \n\n";
 
         if(print_sols)
             phi.print(std::cout);
 
         double l2_abs_error = phi.l2_norm();
 
         double l2_rel_error = l2_abs_error / reference_solution.l2_norm();
 
         if(print_sols){
         std::cout<<  "||Phi_final - Phi_ref||_2 : " << std::setprecision(10)
                 << l2_abs_error
                 << "\n"
                 << "||Phi_final - Phi_ref||_2 / ||Phi_ref||_2 : "
                 << l2_rel_error
                 << std::endl;
 
         convergence_history.add_value("# iter", iter);
 
         convergence_history.add_value("||u - u_h||_2", double(l2_abs_error) );
         convergence_history.set_precision      ("||u - u_h||_2", 16);
         convergence_history.add_value("||u - u_h||_2/||u||_2", double(l2_rel_error) );
         convergence_history.set_precision      ("||u - u_h||_2/||u||_2", 16);
 
         }
     }
 
     {
 
         QString filename = "unit_test_coarse_grid_cg_";
 
         int np = N_POINTS_PHI;
         filename += QString::number(np);
         filename += "_points.dat";
         std::ofstream out(filename.toAscii());
 
         convergence_history.write_text(out);
     }
 
     {
         std::ofstream out("phi_out_coarse.dat");
         phi.print_gnu_plot(out);
     }
 }

  
 template<typename T>
 void step12::CUDADriver<T>::coarse_CG_solver()
 {
     int n_intervals_per_dim = MESH_DIM-1;
     int n_points_per_dim = n_intervals_per_dim+1;
     int n_points = n_points_per_dim * n_points_per_dim * n_points_per_dim;
 
 
     T L = 1.;
 
     T R = .3;
 
     T h = L/n_intervals_per_dim;
 
 
     phi.reinit(n_points);
     {
         std::vector<T> tmp(n_points, 0.);
 
         typename Potential::Base & ref = phi;
         ref = tmp;
     }
 
 
     T tolerance = cg_tol;
 
     typename Potential::Base residual(7*coarse_cg_max_iter+2);
     {
         std::vector<T> tmp(residual.size(), 0.);
         residual = tmp;
     }
 
     coarse_grid_CG_solve(phi.array().val(), n_points_per_dim, tolerance,
                          R, h,
                          coarse_cg_max_iter,
                          residual.array().val());
 
     std::ofstream out("phi_out_coarse.dat");
     phi.print_gnu_plot(out);
 }

  
 template<typename T>
 void step12::CUDAUnitTestDriver<T>::test_gauss_seidel()
 {
     int n_intervals_per_dim = MESH_DIM-1;
     int n_points_per_dim = n_intervals_per_dim+1;
     int n_points = n_points_per_dim * n_points_per_dim * n_points_per_dim;
 
 
     static const bool  print_sols = false;
     static const int max_iter = 50;
     static const double tol = 1e-12;
 
     T L = 1.;
 
     T R = .25;
 
     T h = L/n_intervals_per_dim;
 
     Potential reference_solution, sol_diff;
 
     ::ConvergenceTable convergence_history;
 
     std::vector<T> sol_ref_host(n_points);
     phi.reinit(n_points);
     e_H.reinit(n_points);
     {
         std::vector<T> tmp(n_points);
 
         for (int k = 0; k < n_points; k++)
         {
             sol_ref_host[k] = 1 + std::sin(k);
             tmp[k] =  sol_ref_host[k];
         }
         typename Potential::Base & rs_ref = reference_solution;
         rs_ref = sol_ref_host;
 
         int x, y, z;
 
         for (int i = 0; i < n_points; i++)
         {
             x = i%n_points_per_dim;
             y = (i%(n_points_per_dim*n_points_per_dim))/n_points_per_dim;
             z = i/(n_points_per_dim * n_points_per_dim);
 
             bool boundary =    (x == 0) || (x == n_intervals_per_dim)
                                || (y == 0) || (y == n_intervals_per_dim)
                                || (z == 0) || (z == n_intervals_per_dim);
 
             if (!boundary)
                 tmp[i] = 0;
         }
 
         typename Potential::Base & ref = phi;
         ref = tmp;
     }
 
     std::cout
             << "||Phi_ref||_2 : " << reference_solution.l2_norm()
             << std::endl;
 
     if(print_sols) {
         std::cout
                 << "Phi_ref : " << std::endl;
         reference_solution.print(std::cout);
     }
 
     std::cout
             << "||Phi_0||_2 : " << phi.l2_norm()
             << std::endl;
     std::cout << "Phi_0: \n\n";
 
     if(print_sols)
         phi.print(std::cout);
 
     T tolerance = tol;
     typename Potential::Base residual(7*coarse_cg_max_iter+2);
     {
         std::vector<T> tmp(residual.size(), 0.);
         residual = tmp;
     }
     double l2_abs_error; double l2_rel_error;
 
     CUDATimer gaus_seidel_timer;
     for (int iter = 0; iter < max_iter; iter++)
     {
         gauss_seidel_unit_test(phi.array().val(),
                                n_intervals_per_dim,
                                R,
                                h
                                );
         typename Potential::Base & sol_diff_ref = sol_diff;
         sol_diff_ref = sol_ref_host;
 
         / *sol_diff = phi;* /
         sol_diff -= phi; // reference_solution;
 
         l2_abs_error = sol_diff.l2_norm();
 
         l2_rel_error  = l2_abs_error / reference_solution.l2_norm();
 
         convergence_history.add_value("# iter", iter);
 
         convergence_history.add_value("||u - u_h||_2", double(l2_abs_error) );
         convergence_history.set_precision      ("||u - u_h||_2", 16);
         convergence_history.add_value("||u - u_h||_2/||u||_2", double(l2_rel_error) );
         convergence_history.set_precision      ("||u - u_h||_2/||u||_2", 16);
     }
 
     MG_reference_solution(e_H.array().val(),phi.array().val(),
                           n_intervals_per_dim,
                           h,
                           0.25,
                           true);
 
     gaus_seidel_timer.print_elapsed("Time spent in seidel grid solve : ");
 
     {
         std::ofstream out("phi_out_seidel.dat");
         phi.print_gnu_plot(out);
     }
 
     {
         std::ofstream out("phi_out_seidel_reference.dat");
         e_H.print_gnu_plot(out);
     }
 
     std::cout<<  "||Phi_final||_2 : " << phi.l2_norm()<<std::endl;
 
     std::cout
             << "N Threads : " << N_COARSE_GRID_THREADS
             << ", N elements : " << phi.size();
 
 
 
     std::cout << "Phi: \n\n";
 
     if(print_sols)
         phi.print(std::cout);
 
 
 
     phi -= reference_solution;
 
     std::cout << "Phi_final - Phi_ref: \n\n";
 
     if(print_sols)
         phi.print(std::cout);
 
 
 
 
     std::cout<<  "||Phi_final - Phi_ref||_2 : " << std::setprecision(10)
              << l2_abs_error
              << "\n"
              << "||Phi_final - Phi_ref||_2 / ||Phi_ref||_2 : "
              << l2_rel_error
              << std::endl;
 
     {
 
         QString filename = "unit_test_gauss_seidel_";
 
         int np = N_POINTS_PHI;
         filename += QString::number(np);
         filename += "_points.dat";
         std::ofstream out(filename.toAscii());
 
         convergence_history.write_text(out);
     }
 
 
      std::cout<<  "||Error_final||_2 : " << e_H.l2_norm()<<std::endl;
 
 
 }

  
 template<typename T>
 void step12::CUDAUnitTestDriver<T>::test_Multigrid()
 {
 
     int ncycle = 1;
     int max_level = 1;
 
     int max_iter = 50;
 
     int n_intervals_per_dim;
     int  back;
     bool prolongation;
     int n_points = MESH_DIM * MESH_DIM * MESH_DIM;
     int start_n_points = n_points;
     T tolerance = cg_tol;
     int start_intervals_per_dim = MESH_DIM-1;
     int max_intervals_per_dim = start_intervals_per_dim;
     int last_interval = start_intervals_per_dim;
     int max_n_points = n_points;
 
     for(int i = 0; i<max_level; i++)
     {
         last_interval = last_interval * 2;
         max_intervals_per_dim =last_interval;
         max_n_points += (max_intervals_per_dim+1)
                         *(max_intervals_per_dim+1)
                         *(max_intervals_per_dim+1);
     }
 
 
 
     T * u_h;
     T * u_H;
     T * diff;
     T * e_h;
 
 
 
     T L = 1.;
 
     T sigma = .25;
     T R = .25;
 
     T h = L/start_intervals_per_dim;
 
     printf("whole phi -->  %d\n",max_n_points);
 
     phi.reinit(max_n_points);
     e_H.reinit(max_n_points);
 
     phi *= 0;
     cudaThreadSynchronize();
 
     typename Potential::Base residual(7*coarse_cg_max_iter+2);
     {
         std::vector<T> tmp(residual.size(), 0.);
         residual = tmp;
     }
     u_h = phi.array().val();
     u_H = phi.array().val();
     diff= phi.array().val();
     e_h = e_H.array().val();
 
     n_intervals_per_dim = start_intervals_per_dim;
 
 
     for (int level = 0; level <=max_level; level++)
     {
         for(int n_cycle = ncycle; n_cycle > 0; n_cycle--)
         {
             u_h = phi.array().val();
             u_H = phi.array().val();
             n_points = start_n_points;
 
             for(int up = 1; up <=level; up++)
             {
                 prolongation = true;
 
                 u_H = u_h;
                 u_h +=n_points;
 
 
                 n_intervals_per_dim *= 2 ;
                 h = L/n_intervals_per_dim;
 
                 grid_transfer(u_H, u_h, n_intervals_per_dim, prolongation);
 
                 n_points = (n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1);
 
                 for(int g = 0; g<max_iter; g++)
                     gauss_seidel(u_h, n_intervals_per_dim,h,sigma);
 
                 printf("UPgauss(%d) ", n_points);
                 printf("--> Pro  u_H --> %d , u_h --> %d  \n", u_H-diff, u_h - diff);
 
             }
             for(int down = level; down >0 ; down--)
             {
                 prolongation = false;
 
                 n_intervals_per_dim /= 2 ;
                 back = n_intervals_per_dim /2;
                 h = L/n_intervals_per_dim;
 
                 grid_transfer(u_H, u_h, n_intervals_per_dim, prolongation);
 
                 n_points = (n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1);
 
 
                 if(down == 1){
                     printf("\ncg(%d)-->", n_points);
                     printf("Restr  u_H --> %d , u_h --> %d\n", u_H-diff, u_h-diff);
 
 
 
                     coarse_grid_CG_solve(phi.array().val(), MESH_DIM, tolerance, sigma, h,
                                          coarse_cg_max_iter,
                                          residual.array().val());
 
                 }
                 else{
                     printf("DOWNgauss(%d) --> ", n_points);
                     printf("Restr  u_H --> %d , u_h --> %d\n", u_H-diff, u_h-diff);
 
                     for(int g = 0; g<max_iter; g++)
                         gauss_seidel(u_H, n_intervals_per_dim,h,sigma);
                 }
 
                 u_h = u_H;
                 u_H -=((back+1)*(back+1)*(back+1)) ;
 
             }
 
             if(level == 0 && !(level == 0 && n_cycle != ncycle)){
 
                  coarse_grid_CG_solve(phi.array().val(), MESH_DIM, tolerance, sigma, h,
                                      coarse_cg_max_iter,
                                      residual.array().val());
 
                 printf("cg(%d) ", n_points);
                 printf("First u_H --> %d , u_h --> %d\n", u_H-diff, u_h-diff);
             }
 
             printf("\n");
         }
 
     }
     n_points = start_n_points;
     u_h = phi.array().val();
     n_intervals_per_dim=start_intervals_per_dim;
 
     for(int level = 1; level <=max_level; level++)
     {
         u_H = u_h;
         prolongation = true;
         n_intervals_per_dim *= 2 ;
         h = L/n_intervals_per_dim;
         grid_transfer(u_h, u_H, n_intervals_per_dim, prolongation);
 
 
         u_h +=n_points;
         e_h +=n_points;
 
         n_points = (n_intervals_per_dim+1)
                    *(n_intervals_per_dim+1)
                    *(n_intervals_per_dim+1);
 
         printf("end_gauss(%d) ", n_points);
         printf("--> Pro  U_H --> %d , U_h --> %d \n", u_H-diff, u_h-diff);
 
         for(int g = 0; g<max_iter; g++)
             gauss_seidel(u_h, n_intervals_per_dim,h,sigma);
     }
     printf("\n");
 
     bool reference_or_error;
     reference_or_error = true;
 
     MG_reference_solution(e_h,u_h,n_intervals_per_dim,h,sigma,reference_or_error);
 
     / *std::cout<<phi.l2_norm()<<std::endl;* /
 
 
     std::ofstream out("phi_multi_out.dat");
     phi.print_multigrid_gnu(out, MESH_DIM, max_level);
 
     if(reference_or_error)
     {
         std::ofstream out2("phi_multi_out_reference.dat");
         e_H.print_multigrid_gnu(out2, MESH_DIM, max_level);
 
     }else
     {
         std::ofstream out2("phi_multi_out_error.dat");
         e_H.print_multigrid_gnu(out2, MESH_DIM, max_level);
 
         std::cout<<  "||Final_Error||_2 : " << e_H.l2_norm()<<std::endl;
 
     }
 
 
 
 
 
 }

  
 template<typename T>
 void step12::CUDAUnitTestDriver<T>::test_grid_transfer()
 {
     if (this->__params->transfer_tests.empty())
     {
         std::cout << __FUNCTION__ << ": nothing to be done.\n";
         return;
     }
 
     std::map<QString, Selectors::TransferTestfunction>::const_iterator tf=this->__params->transfer_tests.begin();
 
     for(; tf!=this->__params->transfer_tests.end(); ++tf)
     {
         std::cout << "Testing function : " << tf->first.toStdString() << std::endl;
         this->test_grid_transfer_implementation(tf->second);
     }
 }

  
 template<typename T>
 void  step12::CUDAUnitTestDriver<T>::test_grid_transfer_implementation(Selectors::TransferTestfunction test_function)
 {
 
     int ncycle = 1;
     if(this->__params->n_cycle == "v")
         ncycle = 1;
     else if(this->__params->n_cycle == "w")
         ncycle = 2;
 
     int max_level = this->__params->max_level+1;
 
     int n_intervals_per_dim;
     int  back;
     bool prolongation;
     int n_points = MESH_DIM * MESH_DIM * MESH_DIM;
     int start_n_points = n_points;
     int start_intervals_per_dim = MESH_DIM-1;
     int max_intervals_per_dim = start_intervals_per_dim;
     int last_interval = start_intervals_per_dim;
     int max_n_points = n_points;
     int restriction_first_n_points,first_n_intervals_per_dim;
 
 
     for(int i = 0; i<max_level; i++)
     {
 
         last_interval = last_interval * 2;
         max_intervals_per_dim =last_interval;
         max_n_points += (max_intervals_per_dim+1)
                         *(max_intervals_per_dim+1)
                         *(max_intervals_per_dim+1);
     }
 
     if(this->__params->disp_mem_consumption)
         std::cout << "Estimated memory consumption of all solutions : " << max_n_points * sizeof(T)/(1024*1024*1024.) << " GByte" << std::endl;
 
     T * u_h;
     T * u_H;
     T * diff;
     T L = 1.;
 
 
 
     T H = L/start_intervals_per_dim;
     if(this->__params->disp_phi_max_size)
         printf("whole phi -->  %d\n\n",max_n_points);
 
     phi.reinit(max_n_points);
 
     phi *= 0;
     cudaThreadSynchronize();
 
     u_h = phi.array().val();
     u_H = phi.array().val();
     diff= phi.array().val();
     n_intervals_per_dim = start_intervals_per_dim;
 
     for (int level = 0; level <max_level; level++)
     {
         if(this->__params->disp_current_level)
             printf("current level ---> %d\n", level);
 
 
         for(int n_cycle = ncycle; n_cycle > 0; n_cycle--)
         {
             u_h = phi.array().val();
             u_H = phi.array().val();
 
             n_points = start_n_points;
             n_intervals_per_dim = start_intervals_per_dim;
 
             int current_level = 0; // coarsest level
 
             ::Timer prolongation_timer;
 
             for(int up = 1; up <=level; up++, current_level++)
             {
                 prolongation = true;
 
                 u_H = u_h;
                 u_h +=n_points;
 
                 e_H.reinit(n_points);
 
                 std::vector<T> tmp(n_points,0.);
 
                 typename Potential::Base & e_ref = e_H;
                 e_ref = tmp;
 
                 n_intervals_per_dim *= 2 ;
 
                 T h = H/2;
 
                 prolongation_unit_test(u_H, u_h, e_H.array().val(),
                                        n_intervals_per_dim, h, current_level, test_function);
                 cudaThreadSynchronize();
 
                 if(this->__params->disp_error_matrix)
                     e_H.print(std::cout);
 
                 if(this->__params->disp_pointer)
                     printf("\nPro  u_H --> %d,  u_h --> %d  \n", u_H-diff, u_h - diff);
 
                 if(this->__params->disp_transfer_error)
                     printf("prolongation_error %e \n", e_H.l2_norm() / std::sqrt(e_H.size() ) );
 
                 if(this->__params->disp_transfer_dimension_resize_info)
                     printf("UPtransfer( %d to ", n_points);
 
                 n_points = (n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1);
                 H/=2;
                 if(this->__params->disp_transfer_dimension_resize_info)
                     printf("%d )\n", n_points);
             }
 
 
             if(this->__params->disp_transfer_time)
                 std::cout << "Time elapsed in one prolongation from coarsest to finest grid : "<< prolongation_timer() << "sec." << std::endl;
 
             ::Timer restriction_timer;
             current_level = 0;
             for(int down = level; down >0 ; down--, current_level++)
             {
 
 
                 first_n_intervals_per_dim = n_intervals_per_dim /2;
                 restriction_first_n_points = (first_n_intervals_per_dim+1)
                                              *(first_n_intervals_per_dim+1)
                                              *(first_n_intervals_per_dim+1);
                 e_H.reinit(restriction_first_n_points);
 
                 std::vector<T> tmp(restriction_first_n_points,0.);
 
                 typename Potential::Base & e_ref = e_H;
                 e_ref = tmp;
 
 
                 prolongation = false;
 
                 T h = H;
 
                 restriction_unit_test(u_H, u_h, e_H.array().val(),
                                       n_intervals_per_dim, h, current_level, test_function);
 
 
                 cudaThreadSynchronize();
                 if(this->__params->disp_error_matrix)
                     e_H.print(std::cout);
 
                 if(this->__params->disp_pointer)
                     printf("\nRestr  u_H --> %d,  u_h --> %d  \n", u_H-diff, u_h-diff);
 
                 if(this->__params->disp_transfer_error)
                     printf("restriction_error %e \n", e_H.l2_norm() / std::sqrt(e_H.size() ) );
 
                 if(this->__params->disp_transfer_dimension_resize_info)
                     printf("Downtransfer( %d to ", n_points);
 
                 n_intervals_per_dim /= 2 ;
                 n_points = (n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1)
                            *(n_intervals_per_dim+1);
                 H*=2;
                 if(this->__params->disp_transfer_dimension_resize_info)
                     printf("%d )\n", n_points);
 
 
                 u_h = u_H;
                 back = n_intervals_per_dim /2;
                 u_H -=((back+1)*(back+1)*(back+1));
 
 
 
             }
 
 
             if(this->__params->disp_transfer_time)
                 std::cout << "Time elapsed in one restriction from finest to coarsest grid : "<< restriction_timer() << "sec." << std::endl;
         }
 
     }
     printf("\n");
     if(this->__params->disp_data_matrix)
         phi.print_transfer(std::cout, MESH_DIM, max_level-1 );
 
 
     / *std::cout<<phi.l2_norm()<<std::endl;* /
     / *phi.print(std::cout);* /
 
 }
 
 
 
 
 #endif
 
 
 
 #include <iostream>
 #include <vector>
 #include <QString>
 #include <QStringList>
 #include <map>
 
 #include "cuda_driver_step-12.h"
 
 #include <base/parameter_handler.h>
 
 #include "cuda_driver_step-12.hh"
 
 namespace step12 {

  
     class MyFancySimulation {
 
     public:
 
         MyFancySimulation();
 
         void run_unit_tests();
 
         void run();
 
 
     private:
 
     };
 
 
 }

  
 step12::MyFancySimulation::MyFancySimulation()
 {
 
 }

  
 void step12::MyFancySimulation::run_unit_tests()
 {
 
     std::string prm_filename = "unit_tests.prm";
 
     ::ParameterHandler prm_handler;
 
     SimParam::declare(prm_handler);
 
     prm_handler.read_input (prm_filename);
 
     SimParam params;
 
     params.get(prm_handler);
 
     std::ostringstream logfile_name;
 
     logfile_name << prm_filename << ".log";
 
     std::ofstream out(logfile_name.str().c_str());
 
     prm_handler.print_parameters(out, ::ParameterHandler::Text );
 
 #ifdef USE_SINGLE_PRECISION
     step12::CUDAUnitTestDriver<float>  mg_unit_test(params);
 #else
     step12::CUDAUnitTestDriver<double> mg_unit_test(params);
 #endif
 
 
 
 
 
 
      mg_unit_test.test_Multigrid();
 
     std::cout << "==============   Unit tests Done.   ==============\n\n" << std::endl;
 
 }

  
 void step12::MyFancySimulation::run()
 {
 
 #ifdef USE_SINGLE_PRECISION
     / *step12::CUDADriver<float>  mg_solver(params);* /
 #else
     / *step12::CUDADriver<double> mg_solver(params);* /
 #endif
 
     std::cout << "Fertig.!!!!!!!!!!!!!!!!!!!!" << std::endl;
 }

  
 int main(int / *argc* /, char * / *argv* /[])
 {
     cudaSetDevice(1);
 
     using namespace step12;
     MyFancySimulation machma;
 
     machma.run_unit_tests();
 
     / *machma.run();* /
 }

 



blanc++ documentation generated on Mon Jul 18 12:05:08 2011 by 
doxygen
 1.5.7