Max Wardetzky

I have the pleasure of heading the Discrete Differential Geometry Lab at the University of Goettingen.

Research interests

Applied Geometry, Discrete Differential Geometry, Numerical Analysis, Geometry Processing, Physical Simulation, Computer Graphics.

Contact

Institute of Num. and Appl. Math University of Göttingen Lotzestr. 16-18 37083 Göttingen, Germany

Vox: +49 (0)551 39-26778 Fax: +49 (0)551 39-23944 Net: lastname (at) math.uni-goettingen.de

Publications

Preprints

	Sub-Riemannian Random Walks: From Connections to Retractions Michael Herrmann, Pit Neumann, Simon Schwarz, Anja Sturm, and Max Wardetzky. Abstract: We study random walks on sub-Riemannian manifolds using the framework of retractions, i.e., approximations of normal geodesics. We show that such walks converge to the correct horizontal Brownian motion if normal geodesics are approximated to at least second order. In particular, we (i) provide conditions for convergence of geodesic random walks defined with respect to normal, compatible, and partial connections and (ii) provide examples of computationally efficient retractions, e.g., for simulating anisotropic Brownian motion on Riemannian manifolds. [arXiv]
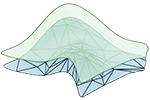
	Generelazing Riemann curvature to Regge metrics Jay Gopalakrishnan, Michael Neunteufel, Joachim Schöberl, and Max Wardetzky. Abstract: In this paper we propose a generalization of the Riemann curvature tensor on manifolds (of dimension two or higher) endowed with a Regge metric. Specifically, while all components of the metric tensor are assumed to be smooth within elements of a triangulation of the manifold, they need not be smooth across element interfaces, where only continuity of the tangential components are assumed. While linear derivatives of the metric can be generalized as Schwartz distributions, similarly generalizing the classical Riemann curvature tensor, a nonlinear second-order derivative of the metric, requires more care. We propose a generalization combining the classical angle defect and jumps of the second fundamental form across element interfaces, and rigorously prove correctness of this generalization. Specifically, if a piecewise smooth metric approximates a globally smooth metric, our generalized Riemann curvature tensor approximates the classical Riemann curvature tensor arising from a globally smooth metric. Moreover, we show that if the metric approximation converges at some rate in a piecewise norm that scales like the L^2-norm, then the curvature approximation converges in the H^{-2}-norm at the same rate, under additional assumptions. By appropriate contractions of the generalized Riemann curvature tensor, this work also provides generalizations of scalar curvature [arXiv]
	A mixed finite element method with piecewise linear elements for the biharmonic equation on surfaces Oded Stein, Eitan Grinspun, Alec Jacobson, and Max Wardetzky. Abstract: The biharmonic equation with Dirichlet and Neumann boundary conditions discretized using the mixed finite element method and piecewise linear functions on triangular elements has been well-studied for domains in R2. Here we study the analogous problem on polyhedral surfaces. In particular, we provide a convergence proof of discrete solutions to the corresponding smooth solution of the biharmonic equation. We obtain convergence rates that are identical to the ones known for the planar setting. Our proof relies on a novel bound for the Linf error of the linear FEM for the Poisson equation on curved surfaces, as well as inverse discrete Laplacians to bound the error between discrete solutions on the surface and the polyhedral mesh approximating it. [arXiv]

Refereed Articles

	Heat kernel asymptotics for scaling limits of isoradial graphs Simon Schwarz, Anja Sturm, and Max Wardetzky. Potential Analysis, 2024. Abstract: We consider the asymptotics of the discrete heat kernel on isoradial graphs for the case where the time and the edge lengths tend to zero simultaneously. Depending on the asymptotic ratio between time and edge lengths, we show that two different regimes arise, corresponding to the short-time asymptotics of the heat kernel on (i) Euclidean spaces and (ii) on graphs. [arXiv] [doi]
	On the improved convergence of lifted distributional Gauss curvature from Regge elements Jay Gopalakrishnan, Michael Neunteufel, Joachim Schöberl, and Max Wardetzky. Results in Applied Mathematics, Vol. 24, pp. 100511, 2024. Abstract: Although Regge finite element functions are not continuous, useful generalizations of nonlinear derivatives like the curvature, can be defined using them. This paper is devoted to studying the convergence of the finite element lifting of a generalized (distributional) Gauss curvature defined using a metric tensor in the Regge finite element space. Specifically, we investigate the interplay between the polynomial degree of the curvature lifting by Lagrange elements and the degree of the metric tensor in the Regge finite element space. Previously, a superconvergence result, where convergence rate of one order higher than expected, was obtained when the metric is the canonical Regge interpolant of the exact metric. In this work, we show that an even higher order can be obtained if the degree of the curvature lifting is reduced by one polynomial degre and if at least linear Regge elements are used. These improved convergence rates are confirmed by numerical examples. [arXiv] [doi]
	Efficient Random Walks on Riemannian Manifolds Michael Herrmann, Simon Schwarz, Anja Sturm, and Max Wardetzky. Foundations of Computational Mathematics, 2023. Abstract: According to a version of Donsker's theorem, geodesic random walks on Riemannian manifolds converge to the respective Brownian motion. From a computational perspective, however, evaluating geodesics can be quite costly. We therefore introduce approximate geodesic random walks based on the concept of retractions. We show that these approximate walks converge to the correct Brownian motion in the Skorokhod topology as long as the geodesic equation is approximated up to second order. As a result we obtain an efficient algorithm for sampling Brownian motion on compact Riemannian manifolds. [arXiv] [doi]
	Analysis of curvature approximations via covariant curl and incompatibility for Regge metrics Jay Gopalakrishnan, Michael Neunteufel, Joachim Schöberl, and Max Wardetzky. SMAI Journal of Computational Mathematics, Vol. 9, pp. 151–195, 2023. Abstract: The metric tensor of a Riemannian manifold can be approximated using Regge finite elements and such approximations can be used to compute approximations to the Gauss curvature and the Levi-Civita connection of the manifold. It is shown that certain Regge approximations yield curvature and connection approximations that converge at a higher rate than previously known. The analysis is based on covariant (distributional) curl and incompatibility operators which can be applied to piecewise smooth matrix fields whose tangential-tangential component is continuous across element interfaces. Using the properties of the canonical interpolant of the Regge space, we obtain superconvergence of approximations of these covariant operators. Numerical experiments further illustrate the results from the error analysis. [arXiv] [doi]
	Variational Convergence of Discrete Elasticae Sebastian Scholtes, Henrik Schumacher, and Max Wardetzky. IMA Journal of Numerical Analysis, Volume 42, Issue 1, pp. 300–332, 2022. Abstract: We discuss a discretization by polygonal lines of the Euler-Bernoulli bending energy and of Euler elasticae under clamped boundary conditions. We show Hausdorff convergence of the set of almost minimizers of the discrete bending energy to the set of smooth Euler elasticae under mesh refinement in (i) the W^{1,∞}-topology for piecewise-linear interpolation and in (ii) the W^{2,p}-topology, p∈[2,∞[, using a suitable smoothing operator to create W^{2,p}-curves from polygons. [arXiv] [doi]
	A Simple Discretization of the Vector Dirichlet Energy Oded Stein, Max Wardetzky, Alec Jacobson, and Eitan Grinspun. Computer Graphics Forum 39(5), pp. 81–92, 2020. Abstract: We present a simple and concise discretization of the covariant derivative vector Dirichlet energy for triangle meshes in 3D using Crouzeix-Raviart finite elements. The discretization is based on linear discontinuous Galerkin elements, and is simple to implement, without compromising on quality: there are two degrees of freedom for each mesh edge, and the sparse Dirichlet energy matrix can be constructed in a single pass over all triangles using a short formula that only depends on the edge lengths, reminiscent of the scalar cotangent Laplacian. Our vector Dirichlet energy discretization can be used in a variety of applications, such as the calculation of Killing fields, parallel transport of vectors, and smooth vector field design. Experiments suggest convergence and suitability for applications similar to other discretizations of the vector Dirichlet energy. [pdf] [doi]
	A Smoothness Energy without Boundary Distortion for Curved Surfaces Oded Stein, Alec Jacobson, Max Wardetzky, and Eitan Grinspun. ACM Transactions on Graphics 39:3, pp. 18:1–18:17, 2020. Abstract: Current quadratic smoothness energies for curved surfaces either exhibit distortions near the boundary due to zero Neumann boundary conditions, or they do not correctly account for intrinsic curvature, which leads to unnatural-looking behavior away from the boundary. This leads to an unfortunate trade-off: one can either have natural behavior in the interior, or a distortion-free result at the boundary, but not both. We introduce a generalized Hessian energy for curved surfaces. This energy features the curved Hessian of functions on manifolds as well as an additional curvature term which results from applying the Weitzenbock identity. Its minimizers solve the Laplace-Beltrami biharmonic equation, correctly accounting for intrinsic curvature, leading to natural-looking isolines. On the boundary, minimizers are as-linear-as-possible, which reduces the distortion of isolines at the boundary. We also provide an implementation that enables the use of the Hessian energy for applications on curved surfaces for which current quadratic smoothness energies do not produce satisfying results, and observe convergence in our experiments. [arXiv] [doi]
	Variational Methods for Discrete Geometric Functionals Henrik Schumacher and Max Wardetzky. In: Handbook of Variational Methods for Nonlinear Geometric Data, edited by Philipp Grohs, Martin Holler, and Andreas Weinmann, Springer, pp. 153–172, 2020. Abstract: While consistent discrete notions of curvatures and differential operators have been widely studied, the question of whether the resulting minimizers converge to their smooth counterparts still remains open for various geometric functionals. Building on tools from variational analysis, and in particular using the notion of Kuratowski convergence, we offer a general framework for treating convergence of minimizers of (discrete) geometric functionals. We show how to apply the resulting machinery to minimal surfaces and Euler elasticae. [doi]
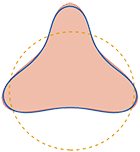
	Discrete Riemannian Calculus on Shell Space Behrend Heeren, Martin Rumpf, Max Wardetzky, and Benedikt Wirth. In: Geometric Partial Differential Equations - Part I, Volume 21 of Handbook of Numerical Analysis, edited by Andrea Bonito Ricardo Nochetto, Elsevier, pp. 621–679, 2020. Abstract: This article discusses a Riemmanian calculus on the space of discrete shells, represented by triangular meshes, and an effective as well as efficient discretization thereof. This calculus comprises shape morphing via geodesic curves, shape extrapolation via the Riemannian exponential map, the transfer of geometric detail via Riemmanian parallel transport, and smooth interpolation of multiple key frames using Riemannian splines. The underlying Riemannian structure is derived from the Hessian of an elastic deformation energy. The discretization is based on an approximation of the Riemmanian path energy via a sum of deformation energies defined on pairs of triangular shapes along a finite sequence of discrete shells. Furthermore, convergence results of all components of the discrete calculus to their continuous counterparts are provided, and a variety of surface processing applications are discussed. [doi]
	Elastic energy regularization for inverse obstacle scattering problems Julian Eckhardt, Ralf Hiptmair, Thorsten Hohage, Henrik Schumacher, and Max Wardetzky. Inverse Problems, Volume 35, Number 10, 104009 (20pp), 2019. Abstract: This paper is motivated by inverse problems in which the boundary curve of a smooth bounded domain has to be reconstructed from indirect measurements. As a classical example we study acoustic inverse obstacle scattering problems for cylindrical sound-soft scatterers using far-field measurements of scattered time-harmonic waves. By introducing a shape manifold as a solution set we allow the reconstruction of general, not necessarily star-shaped, curves. The bending energy is used as a stabilizing term in Tikhonov regularization to gain independence of the parametrization. Moreover, we discuss how self-intersections can be avoided by penalization with the Möbius energy and prove the regularizing property of our approach as well as convergence rates under variational source conditions. In a second part of the paper a discrete setting is introduced, and we describe a numerical method for finding the minimizer of the Tikhonov functional on the shape-manifold. Numerical examples demonstrate that our method can reconstruct non-star-shaped obstacles. [pdf online] [doi]
	Variational Convergence of Discrete Minimal Surfaces Henrik Schumacher and Max Wardetzky. Numerische Mathematik Volume 141, Issue 1, pp. 173–213, 2019. Abstract: Building on and extending tools from variational analysis, we prove Kuratowski convergence of sets of simplicial area minimizers to minimizers of the smooth Douglas-Plateau problem under simplicial refinement. This convergence is with respect to a topology that is stronger than uniform convergence of both positions and surface normals. [pdf online] [arXiv] [doi]
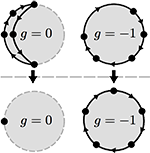
	Natural Boundary Conditions for Smoothing in Geometry Processing Oded Stein, Eitan Grinspun, Max Wardetzky, and Alec Jacobson. ACM Transactions on Graphics 37:2, pp. 23:1–23:13, 2018. Abstract: In geometry processing, smoothness energies are commonly used to model scattered data interpolation, dense data denoising, and regularization during shape optimization. The squared Laplacian energy is a popular choice of energy and has a corresponding standard implementation: squaring the discrete Laplacian matrix. For compact domains, when values along the boundary are not known in advance, this construction bakes in low-order boundary conditions. This causes the geometric shape of the boundary to strongly bias the solution. For many applications, this is undesirable. Instead, we propose using the squared Frobenius norm of the Hessian as a smoothness energy. Unlike the squared Laplacian energy, this energy?s natural boundary conditions (those that best minimize the energy) correspond to meaningful high-order boundary conditions. These boundary conditions model free boundaries where the shape of the boundary should not bias the solution locally. Our analysis begins in the smooth setting and concludes with discretizations using finite diffrences on 2D grids or mixed nite elements for triangle meshes. We demonstrate the core behavior of the squared Hessian as a smoothness energy for various tasks. [pdf] [doi]
	Topology counts: force distributions in circular spring networks Knut M. Heidemann, Andrew O. Sageman-Furnas, Abhinav Sharma, Florian Rehfeldt, Christoph F. Schmidt, and Max Wardetzky. Phys. Rev. Lett. 120, 068001, 2018. Abstract: Filamentous polymer networks govern the mechanical properties of many biological materials. Force distributions within these networks are typically highly inhomogeneous, and, although the importance of force distributions for structural properties is well recognized, they are far from being understood quantitatively. Using a combination of probabilistic and graph-theoretical techniques, we derive force distributions in a model system consisting of ensembles of random linear spring networks on a circle. We show that characteristic quantities, such as the mean and variance of the force supported by individual springs, can be derived explicitly in terms of only two parameters: (i) average connectivity and (ii) number of nodes. Our analysis shows that a classical mean-field approach fails to capture these characteristic quantities correctly. In contrast, we demonstrate that network topology is a crucial determinant of force distributions in an elastic spring network. Our results for 1D linear spring networks readily generalize to arbitrary dimensions. [PRL]
	Topology determines force distributions in one-dimensional random spring networks Knut M. Heidemann, Andrew O. Sageman-Furnas, Abhinav Sharma, Florian Rehfeldt, Christoph F. Schmidt, and Max Wardetzky. Phys. Rev. E, Vol. 97 No. 2, pp. 022306, 2018. Abstract: Networks of elastic fibers are ubiquitous in biological systems and often provide mechanical stability to cells and tissues. Fiber reinforced materials are also common in technology. An important characteristic of such materials is their resistance to failure under load. Rupture occurs when fibers break under excessive force and when that failure propagates. Therefore it is crucial to understand force distributions. Force distributions within such networks are typically highly inhomogeneous and are not well understood. Here we construct a simple one-dimensional model system with periodic boundary conditions by randomly placing linear springs on a circle. We consider ensembles of such networks that consist of N nodes and have an average degree of connectivity z, but vary in topology. Using a graph-theoretical approach that accounts for the full topology of each network in the ensemble, we show that, surprisingly, the force distributions can be fully characterized in terms of the parameters (N,z). Despite the universal properties of such (N,z)-ensembles, our analysis further reveals that a classical mean-field approach fails to capture force distributions correctly. We demonstrate that \emph{network topology} is a crucial determinant of force distributions in elastic spring networks. [arXiv] [doi]
	A Glimpse Into Discrete Differential Geometry Keenan Crane and Max Wardetzky. Notices of the American Mathematical Society, Vol. 64 No. 10, pp. 1153–1159, 2017. Abstract: The emerging field of discrete differential geometry (DDG) studies discrete analogues of smooth geometric objects, providing an essential link between analytical descriptions and computation. In recent years it has unearthed a rich variety of new perspectives on applied problems in computational anatomy/biology, computational mechanics, industrial design, computational architecture, and digital geometry processing at large. The basic philosophy of discrete differential geometry is that a discrete object like a polyhedron is not merely an approximation of a smooth one, but rather a differential geometric object in its own right. In contrast to traditional numerical analysis which focuses on eliminating approximation error in the limit of refinement (e.g., by taking smaller and smaller finite differences), DDG places an emphasis on the so-called “mimetic” viewpoint, where key properties of a system are preserved exactly, independent of how large or small the elements of a mesh might be. Just as algorithms for simulating mechanical systems might seek to exactly preserve physical invariants such as total energy or momentum, structure-preserving models of discrete geometry seek to exactly preserve global geometric invariants such as total curvature. More broadly, DDG focuses on the discretization of objects that do not naturally fall under the umbrella of traditional numerical analysis. This article provides an overview of some of the themes in DDG. [pdf]
	ACM Research Highlight: The Heat Method for Distance Computation Keenan Crane, Clarisse Weischedel, and Max Wardetzky. Communications of the ACM, Vol. 60 No. 11, pp. 90–99, doi: 10.1145/3131280, 2017. Abstract: We introduce the heat method for solving the single- or multiple-source shortest path problem on both flat and curved domains. A key insight is that distance computation can be split into two stages: first find the direction along which distance is increasing, then compute the distance itself. The heat method is robust, efficient, and simple to implement since it is based on solving a pair of standard sparse linear systems. These systems can be factored once and subsequently solved in near-linear time, substantially reducing amortized cost. Real-world performance is an order of magnitude faster than state-of-the-art methods, while maintaining a comparable level of accuracy. The method can be applied in any dimension, and on any domain that admits a gradient and inner production - including regular grids, triangle meshes, and point clouds. Numerical evidence indicates that the method converges to the exact distance in the limit of refinement; we also explore smoothed approximations of distance suitable for applications where greater regularity is desired. [pdf]
	A primer on Laplacians Max Wardetzky. Chapter 5 in: Generalized Barycentric Coordinates in Computer Graphics and Computational Mechanics, K. Horman and N. Sukumar (editors), pp. 77–94, CRC Press, 2017. Abstract: In this chapter we review some important properties of Laplacians, smooth and discrete. We place special emphasis on a unified framework for treating smooth Laplacians on Riemannian manifolds alongside discrete Laplacians on graphs and simplicial manifolds. We cast this framework into the language of linear algebra, with the intent to make this topic as accessible as possible. We combine perspectives from smooth geometry, discrete geometry, spectral analysis, machine learning, numerical analysis, and geometry processing within this unified framework. The connection to generalized barycentric coordinates is established through harmonic functions that interpolate given boundary conditions. [pdf]
	A discrete parametrized surface theory in R^3 Tim Hoffmann, Andrew O. Sageman-Furnas, and Max Wardetzky. International Math Research Notices, Volume 2017, Issue 14, pp. 4217–4258, 2017. Abstract: We propose a discrete surface theory in R^3 that unites the most prevalent versions of discrete special parametrizations. This theory encapsulates a large class of discrete surfaces given by a Lax representation and, in particular, the one-parameter associated families of constant curvature surfaces. The theory is not restricted to integrable geometries, but extends to a general surface theory. [arXiv] [doi]
	Functional Thin Films on Surfaces (Journal verrsion) Orestis Vantzos, Omri Azencot, Max Wardetzky, Martin Rumpf, and Mirela Ben-Chen. IEEE Trans. on Vis. and Comp. Graph. 32(3), pp. 1179–1192, 2017. Abstract: The motion of a thin viscous film of fluid on a curved surface exhibits many intricate visual phenomena, which are challenging to simulate using existing techniques. A possible alternative is to use a reduced model, involving only the temporal evolution of the mass density of the film on the surface. However, in this model, the motion is governed by a fourth-order nonlinear PDE, which involves geometric quantities such as the curvature of the underlying surface, and is therefore difficult to discretize. Inspired by a recent variational formulation for this problem on smooth surfaces, we present a corresponding model for triangle meshes. We provide a discretization for the curvature and advection operators which leads to an efficient and stable numerical scheme, requires a single sparse linear solve per time step, and exactly preserves the total volume of the fluid. We validate our method by qualitatively comparing to known results from the literature, and demonstrate various intricate effects achievable by our method, such as droplet formation, evaporation, droplets interaction and viscous fingering. Finally, we extend our method to incorporate non-linear van der Waals forcing terms which stabilize the motion of the film and allow additional effects such as pearling. [pdf] [supplement]
	Persistence Barcodes versus Kolmogorov Signatures: Detecting Modes of One-Dimensional Signals Ulrich Bauer, Axel Munk, Hannes Sieling, and Max Wardetzky. Found Comput Math. 17:1, pp. 1–33, 2017. Abstract: We investigate the problem of estimating the number of modes (i.e., local maxima) - a well known question in statistical inference - and we show how to do so without presmoothing the data. To this end, we modify the ideas of persistence barcodes by first relating persistence values in dimension one to distances (with respect to the supremum norm) to the sets of functions with a given number of modes, and subsequently working with norms different from the supremum norm. As a particular case we investigate the Kolmogorov norm. We argue that this modification has certain statistical advantages. We offer confidence bands for the attendant Kolmogorov signatures, thereby allowing for the selection of relevant signatures with a statistically controllable error. As a result of independent interest, we show that taut strings minimize the number of critical points for a very general class of functions. We illustrate our results by several numerical examples. [pdf]
	On the incompressibility of cylindrical origami patterns Friedrich Bös, Etienne Vouga, Omer Gottesman, and Max Wardetzky. ASME. J. Mech. Des. 2016, 139(2), pp. 021404–021404-9, 2016. Abstract: The art and science of folding intricate three-dimensional structures out of paper has occupied artists, designers, engineers, and mathematicians for decades, culminating in the design of deployable structures and mechanical metamaterials. Here we investigate the axial compressibility of origami cylinders, i.e., cylindrical structures folded from rectangular sheets of paper. We prove, using geometric arguments, that a general fold pattern only allows for a finite number of isometric cylindrical embeddings. Therefore, compressibility of such structures requires either stretching the material or deforming the folds. Our result considerably restricts the space of constructions that must be searched when designing new types of origami-based rigid-foldable deployable structures and metamaterials. [arXiv] [doi]
	Splines in the Space of Shells Behrend Heeren, Martin Rumpf, Peter Schröder, Max Wardetzky, and Benedikt Wirth. Computer Graphics Forum 35(5), pp. 111–120, 2016. Abstract: Cubic splines in Euclidean space minimize the mean squared acceleration among all curves interpolating a given set of data points. We extend this observation to the Riemannian manifold of discrete shells in which the associated metric measures both bending and membrane distortion. Our generalization replaces the acceleration with the covariant derivative of the velocity. We introduce an effective time-discretization for this novel paradigm for navigating shell space. Further transferring this concept to the space of triangular surface descriptors - edge lengths, dihedral angles, and triangle areas - results in a simplified interpolation method with high computational efficiency. [pdf]
	Functional Thin Films on Surfaces Omri Azencot, Orestis Vantzos, Max Wardetzky, Martin Rumpf, and Mirela Ben-Chen. Proceedings of the ACM Symposium on Computer Animation, Los Angeles, 2015. Best Paper Award (one of three) Abstract: The motion of a thin viscous film of fluid on a curved surface exhibits many intricate visual phenomena, which are challenging to simulate using existing techniques. A possible alternative is to use a reduced model, involving only the temporal evolution of the mass density of the film on the surface. However, in this model, the motion is governed by a fourth-order nonlinear PDE, which involves geometric quantities such as the curvature of the underlying surface, and is therefore difficult to discretize. Inspired by a recent variational formulation for this problem on smooth surfaces, we present a corresponding model for triangle meshes. We provide a discretization for the curvature and advection operators which leads to an efficient and stable numerical scheme, requires a single sparse linear solve per time step, and exactly preserves the total volume of the fluid. We validate our method by qualitatively comparing to known results from the literature, and demonstrate various intricate effects achievable by our method, such as droplet formation, evaporation, droplets interaction and viscous fingering. [pdf] [Video]
	Elasticity of 3D networks with rigid filaments and compliant crosslinks Knut M. Heidemann, Abhinav Sharma, Florian Rehfeldt, Christoph F. Schmidt, and Max Wardetzky. Soft Matter, 11(2), pp. 343–354, 2015. Abstract: Disordered filamentous networks with compliant crosslinks exhibit a low linear elastic shear modulus at small strains, but stiffen dramatically at high strains. Experiments have shown that the elastic modulus can increase by up to three orders of magnitude while the networks withstand relatively large stresses without rupturing. Here, we perform an analytical and numerical study on model networks in three dimensions. Our model consists of a collection of randomly oriented rigid filaments connected by flexible crosslinks that are modeled as wormlike chains. Due to zero probability of filament intersection in three dimensions, our model networks are by construction prestressed in terms of initial tension in the crosslinks. We demonstrate how the linear elastic modulus can be related to the prestress in these networks. Under the assumption of affine deformations in the limit of infinite crosslink density, we show analytically that the nonlinear elastic regime in 1- and 2-dimensional networks is characterized by power-law scaling of the elastic modulus with the stress. In contrast, 3-dimensional networks show an exponential dependence of the modulus on stress. Independent of dimensionality, if the crosslink density is finite, we show that the only persistent scaling exponent is that of the single wormlike chain. We further show that there is no qualitative change in the stiffening behavior of filamentous networks even if the filaments are bending-compliant. Consequently, unlike suggested in prior work, the model system studied here cannot provide an explanation for the experimentally observed linear scaling of the modulus with the stress in filamentous networks. [pdf]
	Geometry Processing from an Elastic Perspective Martin Rumpf and Max Wardetzky. GAMM-Mitt. 37, No. 2, 184–216, 2014. Abstract: Triggered by the development of new hardware, such as laser range scanners for high resolution acquisition of complex geometric objects, new graphics processors for realtime rendering and animation of extremely detailed geometric structures, and novel rapid prototyping equipment, such as 3D printers, the processing of highly resolved complex geometries has established itself as an important area of both fundamental research and impressive applications. Concepts from image processing have been picked up and carried over to curved surfaces, physically based modeling plays a central role, and aspects of computer aided geometry design have been incorporated. This paper aims at highlighting some of these developments, with a particular focus on methods related to the mechanics of thin elastic surfaces. We provide an overview of different geometric representations ranging from polyhedral surfaces over level sets to subdivision surfaces. Furthermore, with an eye on differential-geometric concepts underlying continuum mechanics, we discuss fundamental computational tasks, such as surface flows and fairing, surface deformation and matching, physical simulations, as well as spectral and modal methods in geometry processing. Finally, beyond focusing on single shapes, we describe how spaces of shapes can be investigated using concepts from Riemannian geometry. [pdf]
	Wire Mesh Design Akash Garg, Andrew Sageman-Furnas, Bailin Deng, Yonghao Yue, Eitan Grinspun, Mark Pauly, and Max Wardetzky. ACM Transactions on Graphics 33:4, pp. 66:1–66:12, 2014. Abstract: We present a computational approach for designing wire meshes, i.e., freeform surfaces composed of woven wires arranged in a regular grid. To facilitate shape exploration, we map material properties of wire meshes to the geometric model of Chebyshev nets. This abstraction is exploited to build an efficient optimization scheme. While the theory of Chebyshev nets suggests a highly constrained design space, we show that allowing controlled deviations from the underlying surface provides a rich shape space for design exploration. Our algorithm balances globally coupled material constraints with aesthetic and geometric design objectives that can be specified by the user in an interactive design session. In addition to sculptural art, wire meshes represent an innovative medium for industrial applications including composite materials and architectural faÁades. We demonstrate the effectiveness of our approach using a variety of digital and physical prototypes with a level of shape complexity unobtainable using previous methods. [low-res pdf] [high-res pdf] [Video]
	Exploring the Geometry of the Space of Shells Behrend Heeren, Martin Rumpf, Peter Schröder, Max Wardetzky, and Benedikt Wirth. Computer Graphics Forum 33(5):247–256, 2014. Abstract: We prove both in the smooth and discrete setting that the Hessian of an elastic deformation energy results in a proper Riemannian metric on the space of shells (modulo rigid body motions). Based on this foundation we develop a time- and space-discrete geodesic calculus. In particular we show how to shoot geodesics with prescribed initial data, and we give a construction for parallel transport in shell space. This enables, for example, natural extrapolation of paths in shell space and transfer of large nonlinear deformations from one shell to another with applications in animation, geometric, and physical modeling. Finally, we examine some aspects of curvature on shell space. [pdf]
	Functional Fluids on Surfaces Omri Azencot, Steffen Weiflmann, Maks Ovsjanikov, Max Wardetzky, and Mirela Ben-Chen. Computer Graphics Forum 33(5), pp. 237–246, 2014. Abstract: Fluid simulation plays a key role in various domains of science including computer graphics. While most existing work addresses fluids on bounded Euclidean domains, we consider the problem of simulating the behavior of an incompressible fluid on a curved surface represented as an unstructured triangle mesh. Unlike the commonly used Eulerian description of the fluid using its time-varying velocity field, we propose to model fluids using their vorticity, i.e., by a (time varying) scalar function on the surface. During each time step, we advance scalar vorticity along two consecutive, stationary velocity fields. This approach leads to a variational integrator in the space continuous setting. In addition, using this approach, the update rule amounts to manipulating functions on the surface using linear operators, which can be discretized efficiently using the recently introduced functional approach to vector fields. Combining these time and space discretizations leads to a conceptually and algorithmically simple approach, which is efficient, time-reversible and conserves vorticity by construction. We further demonstrate that our method exhibits no numerical dissipation and is able to reproduce intricate phenomena such as vortex shedding from boundaries. [pdf] [Video]
	Geodesics in Heat: A New Approach to Computing Distance Based on Heat Flow Keenan Crane, Clarisse Weischedel, and Max Wardetzky. ACM Transaction on Graphics 32:5, pp. 152:1–152:11, 2013. Abstract: We introduce the heat method for computing the geodesic distance to a specified subset (e.g., point or curve) of a given domain. The heat method is robust, efficient, and simple to implement since it is based on solving a pair of standard linear elliptic problems. The resulting systems can be prefactored once and subsequently solved in near-linear time. In practice, distance is updated an order of magnitude faster than with state-of-the-art methods, while maintaining a comparable level of accuracy. The method requires only standard differential operators and can hence be applied on a wide variety of domains (grids, triangle meshes, point clouds, etc.). We provide numerical evidence that the method converges to the exact distance in the limit of refinement; we also explore smoothed approximations of distance suitable for applications where greater regularity is required. [pdf]
	A discrete geometric approach for simulating the dynamics of thin viscous threads Basile Audoly, Nicolas Clauvelin, Pierre-Thomas Brun, Miklos Bergou, Eitan Grinspun, Max Wardetzky. Journal of Computational Physics, volume 253, pp. 18–49, 2013. Abstract: We present a numerical model for the dynamics of thin viscous threads based on a discrete, Lagrangian formulation of the smooth equations. The model makes use of a condensed set of coordinates, called the centerline/spin representation: the kinematic constraints linking the centerline?s tangent to the orientation of the material frame is used to eliminate two out of three degrees of freedom associated with rotations. Based on a description of twist inspired from discrete differential geometry and from variational principles, we build a full-fledged discrete viscous thread model, which includes in particular a discrete representation of the internal viscous stress. Consistency of the discrete model with the classical, smooth equations for thin threads is established formally. Our numerical method is validated against reference solutions for steady coiling. The method makes it possible to simulate the unsteady behavior of thin viscous threads in a robust and efficient way, including the combined effects of inertia, stretching, bending, twisting, large rotations and surface tension. [pdf]
	Time-Discrete Geodesics in the Space of Shells Behrend Heeren, Martin Rumpf, Max Wardetzky and Benedikt Wirth. Computer Graphics Forum 31(5), pp. 1755–1764, 2012. Abstract: Building on concepts from continuum mechanics, we offer a computational model for geodesics in the space of thin shells, with a metric that reflects viscous dissipation required to physically deform a thin shell. Different from previous work, we incorporate bending contributions into our deformation energy on top of membrane distortion terms in order to obtain a physically sound notion of distance between shells, which does not require additional smoothing. Our bending energy formulation depends on the so-called relative Weingarten map, for which we provide a discrete analogue based on principles of discrete differential geometry. Our computational results emphasize the strong impact of physical parameters on the evolution of a shell shape along a geodesic path. [pdf]
	Flexible Developable Surfaces Justin Solomon, Etienne Vouga, Max Wardetzky, Eitan Grinspun. Computer Graphics Forum 31(5), pp. 1567–1576, 2012. Abstract: We introduce a discrete paradigm for developable surface modeling. Unlike previous attempts at interactive developable surface modeling, our system is able to enforce exact developability at every step, ensuring that users do not inadvertently suggest configurations that leave the manifold of admissible folds of a flat two-dimensional sheet. With methods for navigation of this highly nonlinear constraint space in place, we show how to formulate a discrete mean curvature bending energy measuring how far a given discrete developable surface is from being flat. This energy enables relaxation of user-generated configurations and suggests a straightforward subdivision scheme that produces admissible smoothed versions of bent regions of our discrete developable surfaces. [pdf]
	Optimal topological simplification of discrete functions on surfaces Ulrich Bauer, Carsten Lange, and Max Wardetzky. Discrete and Computational Geometry 47:2 (2012), 347–377. Abstract: Given a function f on a surface and a tolerance δ > 0, we construct a function fδ subject to ‖fδ - f‖∞ ≤ δ such that fδ has a minimum number of critical points. Our construction relies on a connection between discrete Morse theory and persistent homology and completely removes homological noise with persistence ≤ 2δ from the input function f. The number of critical points of the resulting simplified function fδ achieves the lower bound dictated by the stability theorem of persistent homology. We show that the simplified function can be computed in linear time after persistence pairs have been computed. [pdf] [doi]
	Discrete Laplacians on General Polygonal Meshes Marc Alexa and Max Wardetzky, ACM Transaction on Graphics 30:4 (SIGGRAPH), pp. 102:1–102:10, 2011. Abstract: While the theory and applications of discrete Laplacians on triangulated surfaces are well developed, far less is known about the general polygonal case. We present here a principled approach for constructing geometric discrete Laplacians on surfaces with arbitrary polygonal faces, encompassing non-planar and non-convex polygons. Our construction is guided by closely mimicking structural properties of the smooth Laplace-Beltrami operator. Among other features, our construction leads to an extension of the widely employed cotan formula from triangles to polygons. Besides carefully laying out theoretical aspects, we demonstrate the versatility of our approach for a variety of geometry processing applications, embarking on situations that would have been more difficult to achieve based on geometric Laplacians for simplicial meshes or purely combinatorial Laplacians for general meshes. [pdf] [code]
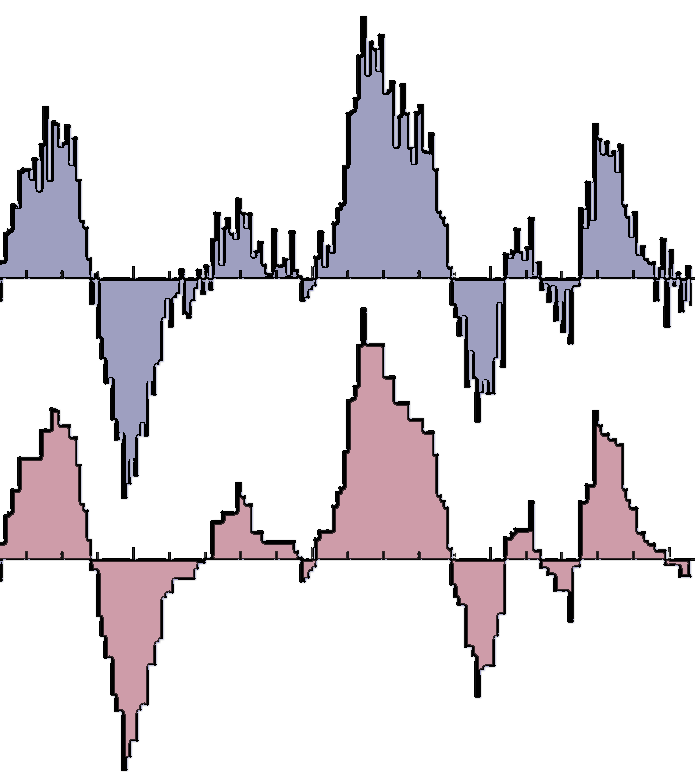
	Total Variation Meets Topological Persistence: A First Encounter Ulrich Bauer, Carola-Bibiane Schönlieb, and Max Wardetzky. Proceedings of ICNAAM 2010, pp. 1022–1026. Abstract: We present first insights into the relation between two popular yet apparently dissimilar approaches to denoising of one dimensional signals, based on (i) total variation (TV) minimization and (ii) ideas from topological persistence. While a close relation between (i) and (ii) might phenomenologically not be unexpected, our work appears to be the first to make this connection precise for one dimensional signals. We provide a link between (i) and (ii) that builds on the equivalence between TV-L2 regularization and taut strings and leads to a novel and efficient denoising algorithm that is contrast preserving and operates in O(nlogn) time, where n is the size of the input. [pdf]
	Discrete Viscous Threads Miklos Bergou, Basile Audoly, Etienne Vouga, Max Wardetzky, Eitan Grinspun, ACM Transaction on Graphics 29:4 (SIGGRAPH), pp. 116:1–116:10, 2010. Abstract: We present a continuum-based discrete model for thin threads of viscous fluid by drawing upon the Rayleigh analogy to elastic rods, demonstrating canonical coiling, folding, and breakup in dynamic simulations. Our derivation emphasizes space-time symmetry, which sheds light on the role of time-parallel transport in eliminating - without approximation - all but an O(n) band of entries of the physical system's energy Hessian. The result is a fast, unified, implicit treatment of viscous threads and elastic rods that closely reproduces a variety of fascinating physical phenomena, including hysteretic transitions between coiling regimes, competition between surface tension and gravity, and the first numerical fluidmechanical sewing machine. The novel implicit treatment also yields an order of magnitude speedup in our elastic rod dynamics. [pdf] [Video]
	Uniform Convergence of Discrete Curvatures from Nets of Curvature Lines Ulrich Bauer, Konrad Polthier, Max Wardetzky, Discrete and Computational Geometry 43:4, 798–823, 2010. Abstract: We study “Steiner-type” discrete curvatures computed from nets of curvature lines on a given smooth surface, and prove their uniform pointwise convergence to smooth principal curvatures. We provide explicit error bounds, with constants depending only on the limit surface and the shape regularity of the discrete net. [pdf] [doi]
	Discrete Elastic Rods Miklos Bergou, Max Wardetzky, Stephen Robinson, Basile Audoly, Eitan Grinspun, ACM Transaction on Graphics 27:3 (SIGGRAPH), pp. 63:1–63:12, 2008. Abstract: We present a discrete treatment of adapted framed curves, parallel transport, and holonomy, thus establishing the language for a discrete geometric model of thin flexible rods with arbitrary cross section and undeformed configuration. Our approach differs from existing simulation techniques in the graphics and mechanics literature both in the kinematic description - we represent the material frame by its angular deviation from the natural Bishop frame - as well as in the dynamical treatment - we treat the centerline as dynamic and the material frame as quasistatic. Additionally, we describe a manifold projection method for coupling rods to rigid-bodies and simultaneously enforcing rod inextensibility. The use of quasistatics and constraints provides an efficient treatment for stiff twisting and stretching modes; at the same time, we retain the dynamic bending of the centerline and accurately reproduce the coupling between bending and twisting modes. We validate the discrete rod model via quantitative buckling, stability, and coupled-mode experiments, and via qualitative knot-tying comparisons. [pdf] [Video]
	Convergence of the Cotangent Formula: An Overview Max Wardetzky, in "Discrete Differential Geometry" (A. I. Bobenko, John M. Sullivan, Peter Schröder, Günter Ziegler, eds.), Birkhäuser Basel, 2008. Abstract: The cotangent formula constitutes an intrinsic discretization of the Laplace- Beltrami operator on polyhedral surfaces in a finite element sense. This note gives an overview of approximation and convergence properties of discrete Laplacians and mean curvature vectors for polyhedral surfaces located in the vicinity of a smooth surface in Euclidean 3-space. In particular, we show that mean curvature vectors converge in the sense of distributions, but fail to converge in L^2. [pdf]
	TRACKS: Toward Directable Thin Shells Miklos Bergou, Saurabh Mathur, Max Wardetzky, Eitan Grinspun, ACM Transaction on Graphics 26:3 (SIGGRAPH), pp. 50:1–50:10, 2007. Abstract: We combine the often opposing forces of artistic freedom and mathematical determinism to enrich a given animation or simulation of a surface with physically based detail. We present a process called tracking, which takes as input a rough animation or simulation and enhances it with physically simulated detail. Building on the foundation of constrained Lagrangian mechanics, we propose weak-form constraints for tracking the input motion. This method allows the artist to choose where to add details such as characteristic wrinkles and folds of various thin shell materials and dynamical effects of physical forces. We demonstrate multiple applications ranging from enhancing an artist's animated character to guiding a simulated inanimate object. [pdf] [Video]
	Discrete Quadratic Curvature Energies Max Wardetzky, Miklos Bergou, David Harmon, Denis Zorin, Eitan Grinspun, Computer Aided Geometric Design (CAGD) 24, 2007, pp. 499–518. Abstract: We present a family of discrete isometric bending models (IBMs) for triangulated surfaces in 3-space. These models are derived from an axiomatic treatment of discrete Laplace operators, using these operators to obtain linear models for discrete mean curvature from which bending energies are assembled. Under the assumption of isometric surface deformations we show that these energies are quadratic in surface positions. The corresponding linear energy gradients and constant energy Hessians constitute an efficient model for computing bending forces and their derivatives, enabling fast time-integration of cloth dynamics with a two- to three-fold net speedup over existing nonlinear methods, and near-interactive rates for Willmore smoothing of large meshes. [pdf] [Video]
	Discrete Laplace operators: No free lunch Max Wardetzky, Saurabh Mathur, Felix Kälberer, Eitan Grinspun, Symposium on Geometry Processing, 2007, pp. 33–37. Abstract: Discrete Laplace operators are ubiquitous in applications spanning geometric modeling to simulation. For robustness and efficiency, many applications require discrete operators that retain key structural properties inherent to the continuous setting. Building on the smooth setting, we present a set of natural properties for discrete Laplace operators for triangular surface meshes. We prove an important theoretical limitation: discrete Laplacians cannot satisfy all natural properties; retroactively, this explains the diversity of existing discrete Laplace operators. Finally, we present a family of operators that includes and extends well-known and widely-used operators. [pdf]
	Cubic Shells Akah Garg, Eitan Grinspun, Max Wardetzky, Denis Zorin, Symposium on Computer Animation, 2007, pp. 91–98. Abstract: Hinge-based bending models are widely used in the physically-based animation of cloth, thin plates and shells. We propose a hinge-based model that is simpler to implement, more efficient to compute, and offers a greater number of effective material parameters than existing models. Our formulation builds on two mathematical observations: (a) the bending energy of curved flexible surfaces can be expressed as a cubic polynomial if the surface does not stretch; (b) a general class of anisotropic materials - those that are orthotropic - is captured by appropriate choice of a single stiffness per hinge. Our contribution impacts a general range of surface animation applications, from isotropic cloth and thin plates to orthotropic fracturing thin shells. [pdf] [Video]
	On the Convergence of Metric and Geometric Properties of Polyhedral Surfaces Klaus Hildebrandt, Konrad Polthier, Max Wardetzky, in Geometriae Dedicata 123, 2006, pp. 89–112. Abstract: We provide conditions for convergence of polyhedral surfaces and their discrete geometric properties to smooth surfaces embedded in Euclidean 3-space. Under the assumption of convergence of surfaces in Hausdorff distance, we show that convergence of the following properties are equivalent: surface normals, surface area, metric tensors, and Laplace-Beltrami operators. Additionally, we derive convergence of minimizing geodesics, mean curvature vectors, and solutions to the Dirichlet problem. [pdf]
	A Quadratic Bending Model for Inextensible Surfaces Miklos Bergou, Max Wardetzky, David Harmon, Denis Zorin, Eitan Grinspun, Symposium on Geometry Processing, 2006, pp. 227–230. Abstract: Efficient computation of curvature-based energies is important for practical implementations of geometric modeling and physical simulation applications. Building on a simple geometric observation, we provide a version of a curvature-based energy expressed in terms of the Laplace operator acting on the embedding of the surface. The corresponding energy, being quadratic in positions, gives rise to a constant Hessian in the context of isometric deformations. The resulting isometric bending model is shown to significantly speed up common cloth solvers, and when applied to geometric modeling situations built on Willmore flow to provide runtimes which are close to interactive rates. [pdf] [Video]
	FreeLence - Coding with free Valences Felix Kälberer, Konrad Polthier, Ulrich Reitebuch, Max Wardetzky, Eurographics (Computer Graphics Forum), 2005, pp. 469–478. Abstract: We introduce FreeLence, a novel and simple single-rate compression coder for triangle manifold meshes. Our method uses free valences and exploits geometric information for connectivity encoding. Furthermore, we introduce a novel linear prediction scheme for geometry compression of 3D meshes. Together, these approaches yield a significant entropy reduction for mesh encoding with an average of 20-30% over leading single-rate region-growing coders, both for connectivity and geometry. [pdf]
	Smooth Feature Lines on Surface Meshes Klaus Hildebrandt, Konrad Polthier, Max Wardetzky, Symposium on Geometry Processing, 2005, pp. 85–90. Abstract: Feature lines are salient surface characteristics. Their definition involves third and fourth order surface derivatives. This often yields to unpleasantly rough and squiggly feature lines since third order derivatives are highly sensitive against unwanted surface noise. The present work proposes two novel concepts for a more stable algorithm producing visually more pleasing feature lines: First, a new computation scheme based on discrete differential geometry is presented, avoiding costly computations of higher order approximating surfaces. Secondly, this scheme is augmented by a filtering method for higher order surface derivatives to improve both the stability of the extraction of feature lines and the smoothness of their appearance. [pdf]

Research Reports and Course Notes

	Variational Convergence of Discrete Minimal Surfaces Max Wardetzky (joint work with Henrik Schumacher), Oberwolfach Reports No. 20/2018. Abstract: Building on and extending tools from variational analysis, we prove Kuratowski convergence of sets of simplicial area minimizers to minimizers of the smooth Douglas-Plateau problem under simplicial refinement. This convergence is with respect to a topology that is stronger than uniform convergence of both positions and surface normals. [pdf]
	Towards a curvature theory for general quad meshes A.O. Sageman-Furnas, Tim Hoffmann, and Max Wardetzky, Oberwolfach Reports No. 13/2015. Abstract: We present a curvature theory for general nonplanar quad meshes (a discrete analogue of smooth parametrized surfaces). As in the smooth setting, the resulting curvatures can be understood both in terms of a Steiner-type offset formula (extending the curvature theory for quad meshes with planar quadrilaterals) and in terms of the first and second fundamental forms. Our curvature theory equips the nonplanar quad meshes that correspond to discrete analogues of surfaces of constant curvature (constructed purely by algebraic means) with the appropriate curvatures. [pdf]
	Convergence of Discrete Elastica Henrik Schumacher, Sebastian Scholtes, Max Wardetzky, Oberwolfach Reports No. 34/2012. Abstract: Using techniques related to the notions of epigraph distance and Attouch-Wets-convergence, we show that under appropriate boundary conditions discrete elastica (i.e., polygonal curves of some fixed length that minimize a certain discrete bending energy) converge to smooth elastica (i.e., smooth curves of some given length that minimize smooth bending energy). [pdf]
	Persistence Simplifiation of Discrete Morse Functions on Surfaces Ulrich Bauer, Carsten Lange, Max Wardetzky, Oberwolfach Reports, Volume 6, Issue 1, 2009. Abstract: We combine the concept of persistent homology with Forman's discrete Morse theory on regular 2-manifold CW complexes to solve the problem of minimizing the number of critical points among all functions within a prescribed distance from a given input function. We give a constructive proof of the tightness of the lower bound on the number of critical points provided by the Stability Theorem of persistent homology. [pdf]
	Geometric Aspects of Discrete Elastic Rods Max Wardetzky, Miklos Bergou, Stephen Robinson, Basile Audoly, Eitan Grinspun, Oberwolfach Reports, Volume 6, Issue 1, 2009. Abstract: Elastic rods are curve-like elastic bodies that have one dimension (length) much larger than the others (cross-section). Their elastic energy breaks down into three contributions: stretching, bending, and twisting. Stretching and bending are captured by the deformation of a space curve called the centerline, while twisting is captured by the rotation of a material frame associated to each point on the centerline. Building on the notions of framed curves, parallel transport, and holonomy, we present a smooth and a corresponding discrete theory that establishes an efficient model for simulating thin flexible rods with arbitrary cross section and undeformed configuration. [pdf]
	Algebraic Topology on Polyhedral Surfaces from Finite Elements Max Wardetzky, Klaus Hildebrandt, Konrad Polthier, Oberwolfach Reports 12/2006. Abstract: We report on a development using piecewise constant vector fields (or one-forms) on compact polyhedral surfaces. The function spaces corresponding to a discrete Hodge decomposition then turn out to be a mixture of conforming and nonconforming linear finite elements. For sequences of polyhedral surfaces whose positions and normals converge to the positions and normals of an embedded compact smooth surface, we report on a convergence result for the corresponding discrete Hodge decompositions and Hodge star operators. [pdf]
	SIGGRAPH ASIA 2008 COURSE NOTES on Discrete Differential Geometry Course Organizors: Eitan Grinspun and Max Wardetzky Abstract: This volume documents the full day course Discrete Differential Geometry: An Applied Introduction at SIGGRAPH Asia 2008 in Singapore on 12 December 2008. These notes supplement the lectures given by Mathieu Desbrun, Peter Schröder, and Max Wardetzky. These notes include contributions by Miklos Bergou, Mathieu Desbrun, Sharif Elcott, Akash Garg, Eitan Grinspun, David Harmon, Eva Kanso, Felix Kälberer, Saurabh Mathur, Ulrich Pinkall, Peter Schröder, Adrian Secord, Boris Springborn, Ari Stern, John M. Sullivan, Yiying Tong, Max Wardetzky, and Denis Zorin, and build on the ideas of many others. [pdf]

Thesis

Discrete Differential Operators on Polyhedral Surfaces - Convergence and Approximation, Max Wardetzky, Dissertation, Freie Universität Berlin, 2006. [dissertation online]

Miscellaneous

Kepler, oranges and shadows from the fourth dimension. ... a site for mathematical entertainment about densest ball packings, disk packings, and their connection to shadows from the 4th dimension. Prepared for the "Beliner Tag der Mathematik 2005" - a day for mathematically interested high-school students.

Blind Dates für die Wissenschaft Brigitte Lutz-Westphal und Max Wardetzky, Mitteilungen der DMV, 2008. Abstract: Wissenschaftlicher Austausch ist eine wichtige Basis für erfolgreiche und innovative Forschung. Das klassische Format von Tagungen und Workshops im Wissenschaftsbetrieb stößt hier immer wieder an seine Grenzen. Insbesondere ist es für den wissenschaftlichen Nachwuchs häufig schwierig, von Vorträgen aus anderen Fachgebieten zu profitieren und so in einen sinnvollen Austausch mit Kolleginnen und Kollegen treten zu können. Für das Berliner DFG-Forschungszentrum MATHEON entwickelten wir ein neues Konzept, um einen vertieften wissenschaftlichen Austausch besser zu fördern. [pdf]