Das Logo zum "Tag der Mathematik 2005" -
Kepler, Apfelsinen und Schatten aus der vierten Dimension
Der Mathematiker und Astronom Johannes Kepler (1571-1630) fragte nach der dichtesten Packung unendlich vieler Kugeln gleicher Größe im Raum. Anders gesagt, wie stapelt man die Kugeln so, dass möglichst wenig Luft zwischen ihnen bleibt?

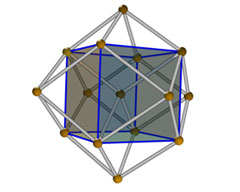
Jeder Obsthändler auf der Straße weiß die dichteste Packung von Kugeln zu sagen: "So wie man Orangen stapelt." Zunächst legt man eine Reihe parallel neben die nächste, so daß jede Orange genau vier weitere berührt. Die Orangen der nächst höheren Schicht werden in die entstehenden Vertiefungen der ersten Schicht gelegt. Diese zweite Schicht hat dann das gleiche Muster wie die erste: jede Orange hat in ihrer Schicht genau vier berührende Nachbarn. Und so fährt man fort.

Kepler Vermutung: Es gibt keine dichtere Packung von Bällen als die des Obsthändlers.

Der Beweis der Kepler Vermutung blieb über Jahrhunderte offen. 1998 legte der Mathematiker Thomas Hales einen 250-seitigen Beweis vor. Dieser baut auf zahlreiche computergestützte Rechnungen auf - und obwohl niemand die Richtigkeit wirklich in Frage stellt - gilt er dennoch bis heute nicht als 100% verifiziert. Wir können hier nicht auf diesen Beweis eingehen - werden aber einige erstaunliche Phänomene besprechen, die mit der Kepler Vermutung in Verbindung stehen.

Das zweidimensionale Problem

Was ist die dichteste Packung kongruenter Kreise in der Ebene? (Überschneidungen sind natürlich nicht erlaubt!)

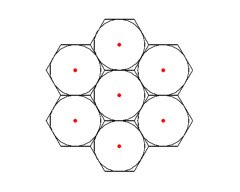Die dichteste Packung kongruenter Kreise in der Ebene ist als Sechseckpackung bekannt. Einen eleganten aber elementaren Beweis dafür erbrachte 1910 der norwegische Mathematiker Axel Thue. Der Name Sechseckpackung rührt daher, daß man um jeden Kreis dieser Packung ein reguläres Sechseck legen kann - derart, daß die gesamte Ebene von solchen Sechsecken lückenlos gepflastert wird.

Die umschreibenden Sechsecke dieser Packung können nun aber auch anders charakterisiert werden: Jedes Sechseck ist die Menge der Punkte, die einen kleineren Abstand zum Mittelpunkt eines jeweiligen Kreises haben, als zu jedem andern Kreismittelpunkt. Allgemeiner, gegeben sei eine Menge isolierter Punkte (P1, P2...) in der Ebene (oder im Raum). Sei P einer dieser Punkte. Dann nennt man die Menge aller der Punkte der Ebene (des Raumes), die einen kleineren Abstand zu P als zu jedem anderen Punkt aus (P1, P2,...) haben, die Voronoi-Zelle von P. Also:

Die Voronoi-Zellen der dichtesten Kreispackung der Ebene sind reguläre Sechsecke.

Reguläre Sechsecke haben noch eine weitere Eigenschaft. Angenommen, man steht in der brennenden Sonne und hat als Schattenspender einzig und allein einen Würfel zur Hand. Wie muss man den Würfel drehen, damit er möglichst viel Schatten spendet? Anders ausgedrückt: Was ist der größte parallele Schatten eines 3-Würfels in der Ebene? Der kleinste Schatten ist sicherlich das Quadrat - und der größte Schatten ist das reguläre Sechseck!

Die Voronoi-Zellen der dichtesten Kreispackung der Ebene sind die größten parallelen Schatten des 3-Würfels.

Das dreidimensionale Problem

Kehren wir zum Kepler Problem zurück. Zunächst beachte man, daß die Sechseckpackung in der Ebene nicht der ersten Schicht der Stapelung von Apfelsinen entspricht. Die Phänomene in Dimension 2 und 3 scheinen also erst einmal verschieden.

Ein Schlüssel zur Gemeinsamkeit der dichtesten Packungen in Dimension 2 und 3 liegt in ihren Voronoi-Zellen. In der Orangenpackung des Obsthändlers hat jede Orange genau 12 berührende Nachbarn im Raum. Die entsprechenden Voronoi-Zellen (mittleres Bild) werden von rhombischen Dodekaedern gebildet. Und analog zu Dimension 2 sind rhombische Dodekaeder die größten parallelen Schatten des 4-Würfels, projiziert in den dreidimensionalen Raum (linkes Bild) - der kleinste Schatten ist natürlich der reguläre 3-Würfel (blau im rechten Bild). Der 4-Würfel ist dabei die Menge aller der Punkte im 4-dimensionalen Raum, deren Koordinaten (x,y,z,w) sämtlich zwischen 0 und 1 liegen.
Die Voronoi-Zellen der dichtesten Kugelpackung des Raumes sind die größten parallelen Schatten des 4-Würfels.

Wie sieht es nun in höheren Dimensionen aus? Gilt dort immer noch, daß die größten Schatten der (n+1)-Würfel, projiziert in den n-dimensionalen Raum, die Voronoi Zellen der dichtesten Packung von n-Kugeln liefern? Die Antwort fällt negativ aus. Schon für n=4 ist das nicht mehr so. Zu weiterführenden Betrachtungen in höheren Dimensionen schaue man beispielsweise auf die Seiten von Gabriele Nebe und Neil Sloane.

Die Bilder auf dieser Seite, sofern synthetisch, wurden mit der 3D Software JavaView erzeugt.

Copyright 2005 Max Wardetzky