The step-4 tutorial program
| Table of contents | |
|---|---|
|
|
Introduction
This example program demonstrates the different features of the BLAS wrappers which are to be used in our CUDA Lab course using a performance evaluation of the QR-factorization as example.
The main purpose of the wrappers is to hide BLAS' API behind some expression templates operating on some taylor-made matrix and vector classes so that, for instance, matrix-vector multiplications can be written in an operator-based form.
BLAS itself is a proposal for a standard API for basic linear algebra operations and started around 1979. In contrast to programming languages like C, C++ or FORTRAN there has never been published an official standard.
The BLAS API basically groups operations according to their run-time complexity into three levels (vector-vector, matrix-vector and matrix-matrix operations) and requires a separate implementation for each precision.
-
Level 1 : vector-vector operations like
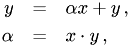
where
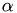is a floating point number and 
, 
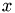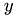are vectors. -
Level 2 : matrix-vector operations like
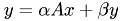
where
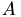is a matrix, , 
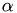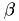are numbers and 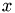, 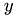are vectors. -
Level 3 : matrix-matrix operations, most notably the ubiquitous generalized matrix-matrix product
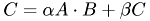
where
, 
, 
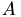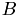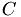are matrices and 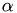, 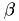are numbers.
It is commonly accepted, that object-oriented programming (OOP) can drastically increase the reusability of solutions of non-trivial subproblems of simulating complex models. Due to the ever growing size and complexity of scientific applications it becomes more and more challenging to ensure software quality, robustness and performance.
Although QR-factorization itself is not really a complex scientific application it is a well-suited example for demonstrating how C++' OOP and template metaprogramming capabilities allow for converting a textbook-style description of an algorithm in an efficient implementation with only a few lines of code. The key point is, that numerical work is delegated to a highly optimized FORTRAN, C or Assembly implementation of the time-critical parts, i.e. the BLAS routines, while OO techniques are used to provide a high-level mathematical description of the algorithm.
The commented program
#ifndef STEP_4_HH #define STEP_4_HH #include <cublas.h> #include <iostream> #include <fstream>
STL header
#include <iostream> #include <vector> #include <numeric>
deal.II
#include <base/convergence_table.h> #include <base/parameter_handler.h> #include <lac/full_matrix.h>
QT
#include <QString> #include <QStringList> #include <QFile> #include <QTextStream>
Driver for GPU part of the program
#include "cuda_driver_step-4.h" #include "cuda_driver_step-4.hh" #include <base/CUDATimer.h> #include <lac/MatrixCreator.h>
cublas++
#include <lac/blas++.h> #include <cmath>
We start the commenting walk through the code of this program by some structures needed for retrieving information about the GPU computing capabilities of the system and defining a simple file-based user interface (UI).
Struct: GlobalData
This structure collects general information about the available graphics cards and upon request displays the most important ones. For more details of the cudaDeviceProp structure have a look a the CUDA reference manual.
struct GlobalData { int n_CUDA_devices; int current_device_id; cudaDeviceProp prop; void cublanc_gpu_info() { const int KB = 1024; const int MB = KB*KB;
Ask for the properties of a GPU with id current_device_id. This attribute must be set before calling this function.
cudaGetDeviceProperties(&prop, this->current_device_id);
printf("Currently used GPU: %s \n",prop.name);
printf("Compute Capability: %d.%d \n",prop.major,prop.minor);
printf("ClockRate: %uMHz \n",prop.clockRate/1000);
printf("Warpsize: %d \n",prop.warpSize);
printf("Number of Multiprocessors: %d \n",prop.multiProcessorCount);
printf("Shared Memory: %uKB\n",prop.sharedMemPerBlock/KB);
printf("Constant Memory: %uKB \n",prop.totalConstMem/KB);
printf("Global Memory: %uMB \n",prop.totalGlobalMem/MB);
printf("the device %s can concurrently copy memory "
"between host and device while executing a kernel\n",
(prop.deviceOverlap? "can": "cannot"));
}
};
For simplicity the GPU data is instantiated as global object.
GlobalData global_data;
Struct: PrecisionName
This is an auxiliary structure for generating precision-dependent filenames for the output of results.
template<typename T> struct PrecisionName { static std::string name(); }; template<> std::string PrecisionName<float>::name() { return "float"; } template<> std::string PrecisionName<double>::name() { return "double"; } template<typename T> std::string PrecisionName<T>::name() { return "unknown_T"; }
The whole project has its own namespace so that it becomes possible to reuse each step in another one even if classes have the same names. Reuse of individual steps into more complex applications is, for instance. demonstrated in step-6 and step-7.
namespace step4 {
Struct: TestUIParamsBase
This structure collects general information about the range of matrix sizes for which a factorization method should be tested. This is not only needed for QR but also for SVD or other matrix factorizations. To reuse this class simply inherit from it.
struct TestUIParamsBase { TestUIParamsBase() {} static void declare(::ParameterHandler & prm); void get(::ParameterHandler & prm);
The following attributes indicate the bounds of the number of colums of the test matrix.
int min_n_cols; int max_n_cols;
To sample the problem sizes we will let the number of rows grow by this factor when looping over the problem sizes in the factorization test.
double n_rows_growth_rate;
The following attribute indicates how many times a test should be repeated in order to compute a reliable average runtime.
int n_repetitions; template <typename T, typename blas> void save_results(const std::string test_name, const ::ConvergenceTable & results_table); private:
To keep the compiler from generating unwanted copy constructors or assignment operators we provide dummy implementations and declare them as private. This will result in a compile-time error if one of them accidentally is invoked.
TestUIParamsBase(const TestUIParamsBase & ) {} TestUIParamsBase & operator = (const TestUIParamsBase & / *other* /) { return *this; } }; } // namespace step4 END
Function: declare
Parameters will be read by an object of type ParameterHandler. This class requires to declare which parameters should be read which is done by this function. For details have a look at the manual of deal.II. This function must be static so that parameters can be declared before the object is instantiated which will hold them.
- Parameters:
-
prm : Object of type ParameterHandler
void step4::TestUIParamsBase::declare(::ParameterHandler & prm) { prm.enter_subsection("Dimensions of test problems."); prm.declare_entry ("log2(min n cols)", "2", ::Patterns::Double(2,12), "Binary logarithm of minimal number of columns of " "upper triangular matrix R. " "Allowed range : [2,12]"); prm.declare_entry ("log2(max n cols)", "3", ::Patterns::Double(2,13), "Binary logarithm of minimal number of columns " "of upper triangular matrix R. " "Allowed range : [3,13]"); prm.declare_entry ("n rows growth rate", "1.2", ::Patterns::Double(1.1,10), "In each test instance the number of rows of R is " "increased by this factor. " "Allowed range : [1.1,10]"); prm.declare_entry("n repetitions", "1", ::Patterns::Integer(1), "Repeat the test for a given matrix size this many times."); prm.leave_subsection(); }
Function: get
- Parameters:
-
prm : Object of type ParameterHandler
void step4::TestUIParamsBase::get(::ParameterHandler & prm) { prm.enter_subsection("Dimensions of test problems."); min_n_cols = pow(2., prm.get_double ("log2(min n cols)") ); max_n_cols = pow(2., prm.get_double ("log2(max n cols)") ); n_rows_growth_rate = prm.get_double("n rows growth rate"); n_repetitions = prm.get_integer("n repetitions"); prm.leave_subsection(); }
Function: save_results
Factorization tests basically create data indicating the relationship between runtime, possibly differentiating w.r.t. different parts of an algorithm, and problem size which can be collected in a deal.II ConvergenceTable. At the end the results will have to be saved to some file. To distinguish different runs the filename should contain some tags indicating what has been tested. For instance, precision or type of GPU used. The analysis is simplified if the names are created according to a fixed format as this makes the composition of the name predictable. In the body of the fucntion you can also see, that QT's string classes are as easy to use as the ones provided by python.
- Parameters:
-
test_name : name of the test, e.g. "QR_test". results_table : table containing the runtime data.
template <typename T, typename blas> void step4::TestUIParamsBase::save_results(const std::string test_name, const ::ConvergenceTable & results_table) { std::string filename(test_name); filename += ("_results_"); filename += blas::name(); filename += "_"; if (blas::name() == "cublas") { printf("Currently used GPU: %s \n", global_data.prop.name); filename += QString(global_data.prop.name).replace(" ", "_").toStdString().c_str(); filename += "_"; } filename += PrecisionName<T>::name(); filename += ".out"; std::ofstream out(filename.c_str());
At the beginning we dump the parameters indicating the range of problem sizes. This makes tests repeatable.
out << "# max n_cols : " << this->max_n_cols << std::endl << "# min n_cols : " << this->min_n_cols << std::endl << "# growth rate : " << this->n_rows_growth_rate << std::endl << std::endl; results_table.write_text(out); } namespace step4 {
Struct: QRTestUIParams
The parameters for testing the QR factorization are completed by the attributes of this structure. A bonus of a file-based user interface is, that it can be easily integrated into a continuous integration testsuite which runs overnight and provides a per-day check whether changes of external libaries have introduced any errors in a program.
struct QRTestUIParams : public TestUIParamsBase { QRTestUIParams() : TestUIParamsBase() {} static void declare(::ParameterHandler & prm); void get(::ParameterHandler & prm);
The following flags indicate which matrices should be dumped to screen for visual inspection.
bool print_Q_orig; bool print_R_orig; bool print_A_orig; bool print_Q ; bool print_R; bool print_QR; bool print_QtQ; bool print_Q_col_errors; private: QRTestUIParams (const QRTestUIParams & / *other* /) : TestUIParamsBase() {} QRTestUIParams & operator = (const QRTestUIParams & / *other* /) { return *this; } }; } // namespace step4 END
Function: declare
- Parameters:
-
prm : Object of type ParameterHandler
void
step4::QRTestUIParams::declare(::ParameterHandler & prm)
{
Start with declaring the basic parameters, that is the range of problem sizes.
TestUIParamsBase::declare(prm);
In a separate subsection we declare the run-time parameters specific to this test.
prm.enter_subsection("Visualization flags."); prm.declare_entry ("print original Q", "false", ::Patterns::Bool(), ""); prm.declare_entry ("print original R", "false", ::Patterns::Bool(), ""); prm.declare_entry ("print original A", "false", ::Patterns::Bool(), "The original A is given multiplying the original " "Q with the original R."); prm.declare_entry ("print Q from factorization", "false", ::Patterns::Bool(), ""); prm.declare_entry ("print R from factorization", "false", ::Patterns::Bool(), ""); prm.declare_entry ("print QR", "false", ::Patterns::Bool(), "Multiplying Q and R as obtained from the factorization " "should give something that closely resembles the original A"); prm.declare_entry ("print QtQ from factorization", "false", ::Patterns::Bool(), "Multiplying the Q obtained from the factorization with " "its own transpose should give a unit matrix."); prm.declare_entry ("print Q column errors", "false", ::Patterns::Bool(), "Computing ||Q_orig - Q||_2 must be done column-wise " "as the individual columns of Q are reproduced only " "up to a sign (the algorithm cannot distinguish " "the direction of a column vector)."); prm.leave_subsection(); }
Function: get
- Parameters:
-
prm : Object of type ParameterHandler
void step4::QRTestUIParams::get(::ParameterHandler & prm) { this->TestUIParamsBase::get(prm); prm.enter_subsection("Visualization flags."); print_Q_orig = prm.get_bool ("print original Q"); print_R_orig = prm.get_bool ("print original R"); print_A_orig = prm.get_bool ("print original A"); print_Q = prm.get_bool ("print Q from factorization"); print_R = prm.get_bool ("print R from factorization"); print_QR = prm.get_bool ("print QR"); print_QtQ = prm.get_bool ("print QtQ from factorization"); print_Q_col_errors = prm.get_bool ("print Q column errors"); prm.leave_subsection(); } namespace step4 {
Class: QRTest
This class manages the performance test. It is responsible for generating test matrices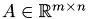 
from a given orthogonal matrix 
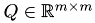and an upper triangular matrix 
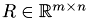. The test is passed if 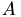can be recovered from the results 
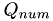and 
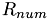of the factorization up to numerical accuracy, i.e.
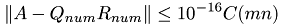
where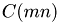 
is a problem-size dependent constant. Division by the problem size then gives an estimate for the element-wise quality of the factorization. The all-govering parameter for the test the number of rows 
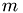, as the set of numbers of columns 
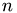is chosen in dependence on that. Then, for each pair 
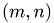a test matrix is generated and the factorization error and runtime is measured. The second template argument makes this class independent of the BLAS implementation.
template <typename T, typename blas> class QRTest { public: typedef typename blas_pp<T, blas>::FullMatrixAccessor FullMatrixAccessor; typedef typename blas_pp<T, blas>::Matrix Matrix; typedef transpose<Matrix> tr; typedef typename blas_pp<T, blas>::SubMatrix SubMatrix; typedef typename blas_pp<T, blas>::MatrixSubCol MatrixSubCol; typedef typename blas_pp<T, blas>::Vector Vector; QRTest(::ParameterHandler & prm); void run(); protected: void check_results(const ::FullMatrix<T> & A, const step4::CudaQRDecomposition<T, blas>& QRf, T elapsed_time); private: void setup_and_assemble(unsigned int nr, unsigned int nc); void factorize(); void save_results(); ::FullMatrix<T> Q, R, H; QRTestUIParams params; ::ConvergenceTable results_table; }; } // namespace step4 END
Constructor: QRTest
- Parameters:
-
prm : ParameterHandler containing the parameter values read from the prm file.
template <typename T, typename blas> step4::QRTest<T, blas>::QRTest(::ParameterHandler & prm) { params.get(prm); }
Function: run
Executes all the individual tests. It is made sure, that the number of rows grows at least by 1. Otherwise we would end up in an infinite loop. The number of columns simply gets doubled until the allowed maximum is reached. The number of rows starts at the current number of columns and grows by the prescribed growth factor or at least by 1 until the maximum number of columns is reached.
template <typename T, typename blas> void step4::QRTest<T, blas>::run() { for (int nc = this->params.min_n_cols; nc < this->params.max_n_cols; nc*=2) for (int nr = nc; nr <= this->params.max_n_cols; nr=std::max(nr+1, int(nr*this->params.n_rows_growth_rate) ) ) { setup_and_assemble(nr, nc); factorize(); } setup_and_assemble(this->params.max_n_cols, this->params.max_n_cols); factorize(); save_results(); }
Function: setup_and_assemble
The matrix Q is initialized by a Hadamard-Matrix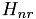 
and R with an upper triangular matrix of width nc.
- Parameters:
-
nr : dimension of Q, i.e. the number of constraints to fulfill in a least-squares problem nc : columns of R, i.e. the number of unknowns.
template <typename T, typename blas> void step4::QRTest<T, blas>::setup_and_assemble(unsigned int nr, unsigned int nc) { Assert(nr >= nc, ::ExcMessage("n_cols must not exceed n_rows.")); int log2_nc = std::log(nc)/std::log(2);
As orthogonal matrix we take a normalized Hadamard matrix. Redundant columns are filled with unit matrix.
MatrixCreator::hadamard(log2_nc, this->H); this->H /= std::sqrt(this->H.n_rows() ); this->Q.reinit(nr, nr);
The upper left diagonal block is filled with the Hadamard matrix ...
for (unsigned int r = 0; r < nc; ++r) for (unsigned int c = 0; c < nc; ++c) Q(r,c) = H(r,c);
and the lower right diagonal block is filled by a unit matrix. In case of a square matrix this block does not exist.
for (unsigned int r = nc; r < nr; ++r) Q(r,r) = 1;
The upper triangular matrix which is to be reconstructed is filled row-wise with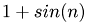 
, 
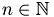where n is continuously increased. Thus, the matrix entries are in the interval 
.
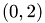this->R.reinit(nr, nc);
int tmp = 1;
for (unsigned int r = 0; r < nr; ++r)
for (unsigned int c = r; c < nc; ++c)
R(r,c) = 1+std::sin(tmp++);
Upon request the original matrices are dumped to screen prior to the factorization.
if (this->params.print_Q_orig) { std::cout << "Initial Q (Hadamard-Matrix, siehe wikipedia): \n"; std::cout << "----------------------------------------------" << std::endl; Q.print(std::cout); } if (this->params.print_R_orig) { std::cout << "\nInitial R : \n"; std::cout << "----------------------------------------------" << std::endl; R.print(std::cout, 12, 5); } if (this->params.print_Q_orig || this->params.print_R_orig) std::cout << std::endl; }
Function: factorize
Create the test matrix A, apply the Householder-based QR-factorization to it and check the results.
template <typename T, typename blas> void step4::QRTest<T, blas>::factorize() { ::FullMatrix<T> A(R.n_rows(), R.n_cols() ); ::FullMatrix<T> Q_orig(Q); Q_orig.mmult(A, R); step4::CudaQRDecomposition<T, blas> QR; T elapsed_time = QR.householder(A); check_results(A, QR, elapsed_time); }
Function: check_results
template <typename T, typename blas> void step4::QRTest<T, blas>::check_results(const ::FullMatrix<T> & A, const step4::CudaQRDecomposition<T, blas>& QRf, T elapsed_time) { int n_rows = QRf.R().n_rows(); int n_cols = QRf.R().n_cols(); std::cout << "n_rows : " << n_rows << ", n_cols : " << n_cols << std::endl;
Check whether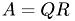 
, 
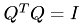is fulfilled. As BLAS usually addresses matrices in column-major order we transpose the input matrix while copying it because in deal.II matrices are stored row-major internally. The FullmatrixAccessor class is needed, as deal.II's FullMatrix class does not grant access to the internal memory so that we need some proxy in order to be able to copy it onto the GPU when using CUBLAS.
FullMatrixAccessor A_t_ugly(A, true / *column-major copy* /); Matrix A_backup; A_backup = A_t_ugly;
We use the verification that the original matrix can be recovered from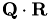 
as an opportunity to test the multiplication of a matrix view with a matrix.
const SubMatrix Q_num(const_cast<Matrix&>(QRf.Q()), 0, 0); const SubMatrix R_num(const_cast<Matrix&>(QRf.R()), 0, 0); Matrix QR(QRf.Q().n_rows(), QRf.R().n_cols()); SubMatrix QR_num(QR, 0, 0); QR_num = Q_num * R_num;
At the end, QtQ should be a diagonal matrix provided QRf.Q() is orthogonal.
Matrix QtQ = tr(QRf.Q()) * QRf.Q();
Compute deviations due to factorization
Matrix A_m_QR;
A_m_QR = A_backup;
A_m_QR -= QR;
T l2_A_QR_error = A_m_QR.l2_norm();
std::cout << "||A -QR||_2 : " << l2_A_QR_error << std::endl;
Up to numerical accuracy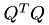 
should recover an identity matrix.
Matrix I;
::IdentityMatrix I_h(n_rows);
I = I_h;
QtQ -= I;
T l2_QtQ_error = QtQ.l2_norm();
std::cout << "||Q^T Q - I||_2 : " << l2_QtQ_error << std::endl;
To determine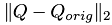 
we have to take care of the signs of the entries. We first compute 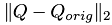column-wise and then we compute the l2-Norm of the vector of the per-column errors.
FullMatrixAccessor Q_t_ugly(Q, true / *column-major copy* /); Matrix Q_orig; Q_orig = Q_t_ugly; T l2_Q_error = 0; for (int c = 0; c < n_cols; ++c) { MatrixSubCol Q_col(const_cast<Matrix&>(QRf.Q()),0,c); MatrixSubCol Q_orig_col(Q_orig,0,c); Q_orig_col -= Q_col; T c_m_err = Q_orig_col.l2_norm();
Undo and change sign.
Q_orig_col += Q_col;
Q_orig_col += Q_col;
T c_p_err = Q_orig_col.l2_norm();
l2_Q_error += std::min(c_m_err, c_p_err);
if (this->params.print_Q_col_errors)
std::cout
<< "Error in col " << c
<< " - : " << c_m_err << ", + : " << c_p_err
<< std::endl;
}
l2_Q_error = std::sqrt(l2_Q_error);
std::cout << "||Q_orig - Q||_2 : " << l2_Q_error << std::endl;
Store errors for later plotting.
this->results_table.add_value("n_rows", n_rows); this->results_table.add_value("n_cols", n_cols); this->results_table.add_value("||A -QR||_2", double(l2_A_QR_error) ); this->results_table.set_precision ("||A -QR||_2", 16); this->results_table.add_value("||Q^T Q - I||_2", double(l2_QtQ_error) ); this->results_table.set_precision ("||Q^T Q - I||_2", 16); this->results_table.add_value("||Q - Q_orig||_2", double(l2_Q_error) ); this->results_table.set_precision ("||Q - Q_orig||_2", 16); this->results_table.add_value("elapsed time", double(elapsed_time) ); this->results_table.set_precision ("elapsed time", 16);
Ausgabe der Matrizen fuer den visuellen Vergleich.
if (this->params.print_Q_orig || this->params.print_R_orig) std::cout << "\nAt this point R and Q are done :" << std::endl; if (this->params.print_Q_orig) { Q_orig = Q_t_ugly; std::cout << "\nQ_orig :" << std::endl; Q_orig.print(); } if (this->params.print_Q) { std::cout << "\nQ_num :" << std::endl; QRf.Q().print(); } if (this->params.print_R) { SubMatrix R_upper_square(const_cast<Matrix&>(QRf.R()), 0, n_cols, 0, n_cols); std::cout << "\nR :" << std::endl; R_upper_square.print(); } if (this->params.print_QtQ) { std::cout << "\nQ^TQ :" << std::endl; QtQ.print(); } if (this->params.print_A_orig) { SubMatrix A_upper_square(A_backup, 0, n_rows, 0, n_cols); std::cout << "\nA_orig :" << std::endl; A_upper_square.print(); } if (this->params.print_QR) { SubMatrix QR_upper_square(QR, 0, n_rows, 0, n_cols); std::cout << "\nQ_num * R_num :" << std::endl; QR_upper_square.print(); } }
Function: save_results
Save the content of results_table in a file in ascii format.
template <typename T, typename blas> void step4::QRTest<T, blas>::save_results() { this->params.template save_results<T, blas>(std::string("QRTest"), results_table); } namespace step4 {
Struct: SimParams
This structure contains all parameters necessary for controling the global test properties, i.e. precision and what BLAS to use.
struct SimUIParams { SimUIParams() {} static void declare(::ParameterHandler & prm); void get(::ParameterHandler & prm); bool run_cublas_float, run_cublas_double; bool run_cpu_blas_float, run_cpu_blas_double; }; } // namespace step4 END
Function: declare
This function informs the ParameterHandler what parameters it should read from the parameter file.
void step4::SimUIParams::declare(::ParameterHandler & prm) { prm.enter_subsection("Global parameters"); prm.declare_entry("Run cublas float", "false", ::Patterns::Bool(), "Single precision is offered by any CUDA-capable GPU."); prm.declare_entry("Run cublas double", "false", ::Patterns::Bool(), "Only available on graphics cards of compute capability " "1.3 and higher"); prm.declare_entry("Run CPU-BLAS float", "false", ::Patterns::Bool(), "Depending on the platform this is either the reference " "BLAS from www.netlib.org or a tuned vendor-specific " "version. For instance Intel's MKL, the Accelerate " "framework by Apple or AMDs ACML."); prm.declare_entry("Run CPU-BLAS double", "false", ::Patterns::Bool(), "Cf. test for floats"); prm.leave_subsection(); }
Function: get
This function must be called in order to transfer the parameters read by the ParameterHandler into the attrbutes of this object.
void step4::SimUIParams::get(::ParameterHandler & prm) { prm.enter_subsection("Global parameters"); run_cublas_float = prm.get_bool("Run cublas float"); run_cublas_double = prm.get_bool("Run cublas double"); run_cpu_blas_float = prm.get_bool("Run CPU-BLAS float"); run_cpu_blas_double = prm.get_bool("Run CPU-BLAS double"); prm.leave_subsection(); } namespace step4 {
Function: run_qr_tests
Process user input and run the tests.
void run_qr_tests(int / *argc* /, char *argv[]) {
Deklariere Parameter und lese aus einer Datei, die genauso heisst wie das Programm erweitert um die Endung ".prm". Die gelesenen Parameter werden in eine log-Datei geschrieben.
First we declare the parameters to expect ...
::ParameterHandler prm_handler;
SimUIParams::declare(prm_handler);
QRTestUIParams::declare(prm_handler);
... then read them from a file residing in the same directory as the binary and with a name starting with the program's name.
std::string prm_filename(argv[0]);
prm_filename += "-QR.prm";
prm_handler.read_input (prm_filename);
prm_filename += ".log";
std::ofstream log_out_text(prm_filename.c_str());
prm_handler.print_parameters (log_out_text,
::ParameterHandler::Text);
SimUIParams params;
params.get(prm_handler);
for(int DevNo = 0; DevNo < global_data.n_CUDA_devices; DevNo++)
{
cudaSetDevice(DevNo);
global_data.current_device_id = DevNo;
global_data.cublanc_gpu_info();
if (params.run_cublas_float) {
std::cout << "Householder-QR<float> using cublas :\n"
<< "------------------------------------------------"
<< std::endl;
Test cublas
QRTest<float, cublas> cublas_qr_test_float(prm_handler);
cublas_qr_test_float.run();
std::cout << "\nHouseholder-QR<float> using cublas DONE \n"
<< "------------------------------------------------\n"
<< std::endl;
}
If double precision is available the corresponding tests are compiled in, too.
#ifdef CUDA_DOUBLE_CAPABLE if (params.run_cublas_double) { std::cout << "\nHouseholder-QR<double> using cublas :\n" << "------------------------------------------------" << std::endl; QRTest<double, cublas> cublas_qr_test_double(prm_handler); cublas_qr_test_double.run(); std::cout << "\nHouseholder-QR<double> using cublas DONE \n" << "------------------------------------------------\n" << std::endl; } #endif }
An almost verbatim copy of the preceeding lines gives the tests for the CPU version.
if (params.run_cpu_blas_float) { std::cout << "\nHouseholder-QR<float> using ATLAS/CBLAS :\n" << "------------------------------------------------" << std::endl;
Test fuer blas
QRTest<float, blas> blas_qr_test_float(prm_handler);
blas_qr_test_float.run();
std::cout
<< "\nHouseholder-QR<float> using ATLAS/CBLAS DONE \n"
<< "------------------------------------------------\n"
<< std::endl;
}
if (params.run_cpu_blas_double) {
std::cout
<< "\nHouseholder-QR<double> using ATLAS/CBLAS :\n"
<< "------------------------------------------------"
<< std::endl;
QRTest<double, blas> blas_qr_test_double(prm_handler);
blas_qr_test_double.run();
std::cout
<< "\nHouseholder-QR<double> using ATLAS/CBLAS DONE \n"
<< "------------------------------------------------\n"
<< std::endl;
}
}
} // namespace step4 END
#endif // STEP_4_HH
#ifndef CUDADriver_STEP_4_H
#define CUDADriver_STEP_4_H
deal.II classes
#include <lac/full_matrix.h>
lab course related headers.
#include <lac/blas++.h> #include <lac/cublas_algorithms.h>
The declaration of the interface to the CUDA-backend are all contained in the following header.
#include "cuda_kernel_wrapper_step-4.cu.h" namespace step4 {
Class: CudaQRDecomposition
QR factorization using Householder transformations. After the factorization Q_d and R_d contain the results.
- Parameters:
-
T : the number type. Althoug it could be any of real or complex floats or doubles we assume that only the real versions are used. blas : must be one of the BLAS wrapper types.
template <typename T, typename blas> class CudaQRDecomposition { public:
Some abbreviations
typedef blas_pp<T, blas> BLAS; typedef typename BLAS::blas_wrapper_type BW; typedef typename BLAS::FullMatrixAccessor FullMatrixAccessor; typedef typename BLAS::Matrix Matrix; typedef typename BLAS::SubMatrix SubMatrix; typedef typename BLAS::MatrixSubCol MatrixSubCol; typedef typename BLAS::Vector Vector; typedef typename BLAS::SubColVector SubColVector; typedef typename BLAS::SubVectorBase SubVectorBase; CudaQRDecomposition(); ~CudaQRDecomposition (); T householder (const ::FullMatrix<T>& A); T lapack_based(const ::FullMatrix<T> &A); const Matrix & Q() const { return Q_d; } const Matrix & R() const { return R_d; } private: Matrix Q_d, R_d; void check_matrix_dimensions(const ::FullMatrix<T>& A); }; } // namespace step4 END #endif // CUDADriver_STEP_4_H #ifndef CUDA_DRIVER_STEP_4_HH #define CUDA_DRIVER_STEP_4_HH #include "cuda_driver_step-4.h"
Header containing the declarations of the wrapper functions - not the kernels. This header is the interface between the CUDA part compiled by nvcc and the host part compiled by gcc.
#include "cuda_kernel_wrapper_step-4.cu.h" #include <cutil_inline.h> #include <iomanip> #include <cmath> #include <QtGlobal> #include <base/sign.h> #include <base/CUDATimer.h> #include <lac/expression_template.h> #include <lac/FullMatrixAccessor.h> #include <lac/cublas_algorithms.h>
Implementation: CudaQRDecomposition Methods
Constructor: CudaQRDecomposition
The CTor of the driver class initializes the BLAS library.
template <typename T, typename blas> step4::CudaQRDecomposition<T, blas>::CudaQRDecomposition() { BW::Init(); }
Destructor: CudaQRDecomposition
Shutdown the BLAS library.
template <typename T, typename blas> step4::CudaQRDecomposition<T, blas>::~CudaQRDecomposition() { BW::Shutdown(); }
Function: check_matrix_dimensions
Our QR factorization requires that the matrix which is to be factorized has more rows than columns. This is checked in this function and in case this requirement is not an exception is thrown. In debug mode the program aborts whereas in release mode you could catch the exception and try to somehow save the computation.
- Parameters:
-
A : Matrix to check.
template <typename T, typename blas> void step4::CudaQRDecomposition<T, blas>::check_matrix_dimensions(const ::FullMatrix<T>& A) { const bool is_matrix_dim_correct = A.n_rows() >= A.n_cols(); #ifdef QT_NO_DEBUG AssertThrow(is_matrix_dim_correct, ::ExcMessage("n_rows must be greater n_cols") ); #else Assert(is_matrix_dim_correct, ::ExcMessage("n_rows must be greater n_cols") ); #endif }
Function: householder
As above we have to take the transpose copy of the input matrix. By having this function accepting a deal.II FullMatrix we enforce this conversion so that on both sides the storage format for the matrix which is to be factorized is unambiguous. Outside of this function it is row-major and inside column-major. The function returns the time needed for the factorization excluding the time needed for memory transfers.
- Parameters:
-
A : matrix to factorize.
template <typename T, typename blas> T step4::CudaQRDecomposition<T, blas>::householder(const ::FullMatrix<T> &A) {
Check, whether there are more rows than columns. Otherwise the factorization cannot be performed.
check_matrix_dimensions(A);
Local variables for some frequently used properties of A.
int n_rows = A.n_rows(); int n_cols = A.n_cols();
Unnecessary copies are ugly hence the name.
::FullMatrixAccessor<T> A_t_ugly(A, true / * transpose copy* /);
Reinitialize the device representation Q_d, R_d of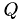 
and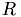 
. During the factorization 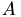is overwritten with 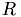thus we put the original 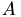into R_d right away. Now copy from host to device.
this->R_d = A_t_ugly;
Identity matrix for image space. This initializes .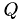
::IdentityMatrix eye_image(n_rows);
Q_d = eye_image;
T alpha = 0, sigma = 0;
Vector x(n_rows);
Vector u(n_rows);
Vector k(n_rows);
SubMatrix A_rest(R_d, 0, 0);
transpose<SubMatrix> A_rest_T (A_rest);
SubMatrix Q_0c(Q_d, 0, 0);
CUDATimer timer;
Eliminate column-wise all entries below the diagonal by Householder reflections.
for(int c=0; c<n_cols-1; c++) {
Move the upper left corner of the view to the next diagonal element.
A_rest.reset(c, n_rows, c, n_cols);
For 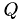we have to mask all previously processed columns.
Q_0c.reset(0, n_rows, c, n_rows);
Store the current diagonal element.
T A_tt1 = R_d(c, c);
The non-zero part of the column Householder vector is initialized with the subcolumn of A.
MatrixSubCol sub_col_A(R_d, c, c);
Compute the i-th Householder vektor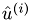 
{
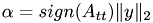
alpha = sign(A_tt1) * sub_col_A.l2_norm();
T beta_t = A_tt1 + alpha;
If the following condition holds, the subcolumn is already zero and there is nothing to do.
if (std::fabs(alpha) < 1e-14) continue; sigma = beta_t/alpha; u = sub_col_A; // std::cout << "u :\n"; u.print(); u.add(c, alpha); // std::cout << "u("<<c<<") + alpha :\n"; u.print(); Assert(std::fabs(beta_t) > 1e-14, ::ExcMessage("Div by 0!") ); u *= 1./beta_t; }
The matrix-matrix product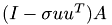 
for updated the remaing part of A is replaced by
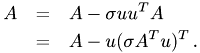
To do this, we define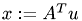 
x = A_rest_T * u;
and take into account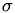 
in the outer product which due to the use of SubMatrixViews is executed only on the truly affected part.
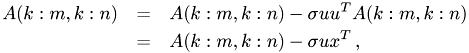
A_rest.add_scaled_outer_product(-sigma, u, x);
Updating 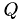is similar
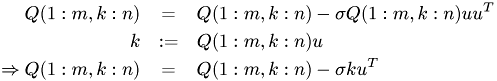
k = Q_0c * u;
Q_0c.add_scaled_outer_product(-sigma, k, u);
}
timer.print_elapsed("Time spent on Householder-QR excluding host-device memory traffic : ");
return timer.elapsed();
}
Function: lapack_based
To have some competition we also implement a wrapper fucntion for calling the QR-factorization provided by LAPACK.
template <typename T, typename blas> T step4::CudaQRDecomposition<T, blas>::lapack_based(const ::FullMatrix<T> &A) { #ifdef USE_LAPACK FullMatrixAccessor A_t_ugly(A, true / *transpose while copying* /); __CLPK_integer m = A_t_ugly.n_rows(); __CLPK_integer n = A_t_ugly.n_cols(); __CLPK_integer lda = A_t_ugly.n_rows(); __CLPK_integer lwork = -1; __CLPK_integer info; std::vector<float> tau(std::min(A_t_ugly.n_rows(), A_t_ugly.n_cols())); std::vector<float> work(1); float * A_val = const_cast<float*>(A_t_ugly.val()); sgeqrf_(&m, &n, A_val, &lda, &tau[0], &work[0], &lwork, &info); if (info != 0) { printf("sgeqrf failed with error code %d\n", (int)info); return 0; } lwork = work[0]; work.resize(lwork); sgeqrf_(&m, &n, A_val, &lda, &tau[0], &work[0], &lwork, &info); if (info != 0) { printf("sgeqrf failed with error code %d\n", (int)info); return 0; } this->R_d = A_t_ugly; #endif } #endif // CUDA_DRIVER_STEP_4_HH #ifndef CUDA_KERNEL_STEP_4_CU_H #define CUDA_KERNEL_STEP_4_CU_H
Declarations of Kernel-Wrapper Functions
#endif // CUDA_KERNEL_STEP_4_CU_H
Header for CUDA utilities.
#include <cutil_inline.h>
Header containing the declarations of the wrapper functions - not the kernels. This header is the interface between the coda compiled by nvcc and the one compiled by gcc.
#include <cuda_kernel_wrapper_step-4.cu.h>
Device Functions
Kernel
Kernel Wrapper Functions
#include "step-4.hh"
Function: main
Hier werden die Benutzereingaben verarbeitet und an die Tests uebergeben.
int main(int argc, char *argv[]) { cudaGetDeviceCount(&global_data.n_CUDA_devices); std::cout << "N available CUDA devices : " << global_data.n_CUDA_devices << std::endl; step4::run_qr_tests(argc, argv); std::cout << std::endl; }
Results
Starting the program with the default parameters QRTest<float> will produce the following output (provided it runs on a machine with a GeForce 8600M GT). Different GPUs will result in different timings, but entries of the factorized matrices should be the same.
Using device 0: GeForce 8600M GT Initial Q : ------------------------------------------------- 0.5 0.5 0.5 0.5 0.5 -0.5 0.5 -0.5 0.5 0.5 -0.5 -0.5 0.5 -0.5 -0.5 0.5
Initial R :
-------------------------------------------------
1.8 1.9 1.1 0.24
00.041 0.72 1.7
0 0 2 1.4
0 0 0 0.46
cublas init succeeded n_rows : 4, n_cols : 4 ||A -QR||_2 : 6.3e-07 ||Q^T Q - I||_2 : 3e-07 Error in col 0 - : 2, + : 0 Error in col 1 - : 2e-06, + : 2 Error in col 2 - : 1.5e-06, + : 2 Error in col 3 - : 1.5e-06, + : 2 ||Q_orig - Q||_2 : 0.0022
An dieser Stelle sind R und Q fertig :
Q_orig :
Matrix dims : 4 4
0.5 0.5 0.5 0.5
0.5 -0.5 0.5 -0.5
0.5 0.5 -0.5 -0.5
0.5 -0.5 -0.5 0.5
Q :
Matrix dims : 4 4
-0.5 0.5 0.5 0.5
-0.5 -0.5 0.5 -0.5
-0.5 0.5 -0.5 -0.5
-0.5 -0.5 -0.5 0.5
R :
-1.841 -1.909 -1.141 -0.2432
0 0.04108 0.7206 1.657
0 0 1.989 1.412
0 -1.863e-09 -2.384e-07 0.456
Q^TQ :
Matrix dims : 4 4
0 0 0 1.49e-08
0 -2.384e-07 0 -4.47e-08
0 0 -1.192e-07 -1.49e-08
1.49e-08 -4.47e-08 -1.49e-08 -1.192e-07
A :
0.9207 0.9752 1.926 1.884
0.9207 0.9341 1.205 -0.2288
0.9207 0.9752 -0.06383 0.01604
0.9207 0.9341 -0.7844 -1.185
QR :
0.9207 0.9752 1.926 1.884
0.9207 0.9341 1.205 -0.2288
0.9207 0.9752 -0.06383 0.01604
0.9207 0.9341 -0.7844 -1.185
Initial Q :
-------------------------------------------------
0.5 0.5 0.5 0.5 0
0.5 -0.5 0.5 -0.5 0
0.5 0.5 -0.5 -0.5 0
0.5 -0.5 -0.5 0.5 0
0 0 0 0 1
Initial R :
-------------------------------------------------
1.8 1.9 1.1 0.24
00.041 0.72 1.7
0 0 2 1.4
0 0 0 0.46
0 0 0 0
cublas init succeeded n_rows : 5, n_cols : 4 ||A -QR||_2 : 6.3e-07 ||Q^T Q - I||_2 : 3e-07 Error in col 0 - : 2, + : 0 Error in col 1 - : 2e-06, + : 2 Error in col 2 - : 1.5e-06, + : 2 Error in col 3 - : 1.5e-06, + : 2 ||Q_orig - Q||_2 : 0.0022
An dieser Stelle sind R und Q fertig :
Q_orig :
Matrix dims : 5 5
0.5 0.5 0.5 0.5 0
0.5 -0.5 0.5 -0.5 0
0.5 0.5 -0.5 -0.5 0
0.5 -0.5 -0.5 0.5 0
0 0 0 0 1
Q :
Matrix dims : 5 5
-0.5 0.5 0.5 0.5 0
-0.5 -0.5 0.5 -0.5 0
-0.5 0.5 -0.5 -0.5 0
-0.5 -0.5 -0.5 0.5 0
0 0 0 0 1
R :
-1.841 -1.909 -1.141 -0.2432
0 0.04108 0.7206 1.657
0 0 1.989 1.412
0 -1.863e-09 -2.384e-07 0.456
Q^TQ :
Matrix dims : 5 5
0 0 0 1.49e-08 0
0 -2.384e-07 0 -4.47e-08 0
0 0 -1.192e-07 -1.49e-08 0
1.49e-08 -4.47e-08 -1.49e-08 -1.192e-07 0
0 0 0 0 0
A :
0.9207 0.9752 1.926 1.884
0.9207 0.9341 1.205 -0.2288
0.9207 0.9752 -0.06383 0.01604
0.9207 0.9341 -0.7844 -1.185
QR :
0.9207 0.9752 1.926 1.884
0.9207 0.9341 1.205 -0.2288
0.9207 0.9752 -0.06383 0.01604
0.9207 0.9341 -0.7844 -1.185
Initial Q :
-------------------------------------------------
0.5 0.5 0.5 0.5 0 0
0.5 -0.5 0.5 -0.5 0 0
0.5 0.5 -0.5 -0.5 0 0
0.5 -0.5 -0.5 0.5 0 0
0 0 0 0 1 0
0 0 0 0 0 1
Initial R :
-------------------------------------------------
1.8 1.9 1.1 0.24
00.041 0.72 1.7
0 0 2 1.4
0 0 0 0.46
0 0 0 0
0 0 0 0
cublas init succeeded n_rows : 6, n_cols : 4 ||A -QR||_2 : 6.3e-07 ||Q^T Q - I||_2 : 3e-07 Error in col 0 - : 2, + : 0 Error in col 1 - : 2e-06, + : 2 Error in col 2 - : 1.5e-06, + : 2 Error in col 3 - : 1.5e-06, + : 2 ||Q_orig - Q||_2 : 0.0022
An dieser Stelle sind R und Q fertig :
Q_orig :
Matrix dims : 6 6
0.5 0.5 0.5 0.5 0 0
0.5 -0.5 0.5 -0.5 0 0
0.5 0.5 -0.5 -0.5 0 0
0.5 -0.5 -0.5 0.5 0 0
0 0 0 0 1 0
0 0 0 0 0 1
Q :
Matrix dims : 6 6
-0.5 0.5 0.5 0.5 0 0
-0.5 -0.5 0.5 -0.5 0 0
-0.5 0.5 -0.5 -0.5 0 0
-0.5 -0.5 -0.5 0.5 0 0
0 0 0 0 1 0
0 0 0 0 0 1
R :
-1.841 -1.909 -1.141 -0.2432
0 0.04108 0.7206 1.657
0 0 1.989 1.412
0 -1.863e-09 -2.384e-07 0.456
Q^TQ :
Matrix dims : 6 6
0 0 0 1.49e-08 0 0
0 -2.384e-07 0 -4.47e-08 0 0
0 0 -1.192e-07 -1.49e-08 0 0
1.49e-08 -4.47e-08 -1.49e-08 -1.192e-07 0 0
0 0 0 0 0 0
0 0 0 0 0 0
A :
0.9207 0.9752 1.926 1.884
0.9207 0.9341 1.205 -0.2288
0.9207 0.9752 -0.06383 0.01604
0.9207 0.9341 -0.7844 -1.185
QR :
0.9207 0.9752 1.926 1.884
0.9207 0.9341 1.205 -0.2288
0.9207 0.9752 -0.06383 0.01604
0.9207 0.9341 -0.7844 -1.185
Initial Q :
-------------------------------------------------
0.5 0.5 0.5 0.5 0 0 0
0.5 -0.5 0.5 -0.5 0 0 0
0.5 0.5 -0.5 -0.5 0 0 0
0.5 -0.5 -0.5 0.5 0 0 0
0 0 0 0 1 0 0
0 0 0 0 0 1 0
0 0 0 0 0 0 1
Initial R :
-------------------------------------------------
1.8 1.9 1.1 0.24
00.041 0.72 1.7
0 0 2 1.4
0 0 0 0.46
0 0 0 0
0 0 0 0
0 0 0 0
cublas init succeeded n_rows : 7, n_cols : 4 ||A -QR||_2 : 6.3e-07 ||Q^T Q - I||_2 : 3e-07 Error in col 0 - : 2, + : 0 Error in col 1 - : 2e-06, + : 2 Error in col 2 - : 1.5e-06, + : 2 Error in col 3 - : 1.5e-06, + : 2 ||Q_orig - Q||_2 : 0.0022
An dieser Stelle sind R und Q fertig :
Q_orig :
Matrix dims : 7 7
0.5 0.5 0.5 0.5 0 0 0
0.5 -0.5 0.5 -0.5 0 0 0
0.5 0.5 -0.5 -0.5 0 0 0
0.5 -0.5 -0.5 0.5 0 0 0
0 0 0 0 1 0 0
0 0 0 0 0 1 0
0 0 0 0 0 0 1
Q :
Matrix dims : 7 7
-0.5 0.5 0.5 0.5 0 0 0
-0.5 -0.5 0.5 -0.5 0 0 0
-0.5 0.5 -0.5 -0.5 0 0 0
-0.5 -0.5 -0.5 0.5 0 0 0
0 0 0 0 1 0 0
0 0 0 0 0 1 0
0 0 0 0 0 0 1
R :
-1.841 -1.909 -1.141 -0.2432
0 0.04108 0.7206 1.657
0 0 1.989 1.412
0 -1.863e-09 -2.384e-07 0.456
Q^TQ :
Matrix dims : 7 7
0 0 0 1.49e-08 0 0 0
0 -2.384e-07 0 -4.47e-08 0 0 0
0 0 -1.192e-07 -1.49e-08 0 0 0
1.49e-08 -4.47e-08 -1.49e-08 -1.192e-07 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
A :
0.9207 0.9752 1.926 1.884
0.9207 0.9341 1.205 -0.2288
0.9207 0.9752 -0.06383 0.01604
0.9207 0.9341 -0.7844 -1.185
QR :
0.9207 0.9752 1.926 1.884
0.9207 0.9341 1.205 -0.2288
0.9207 0.9752 -0.06383 0.01604
0.9207 0.9341 -0.7844 -1.185
Initial Q :
-------------------------------------------------
0.5 0.5 0.5 0.5 0 0 0 0
0.5 -0.5 0.5 -0.5 0 0 0 0
0.5 0.5 -0.5 -0.5 0 0 0 0
0.5 -0.5 -0.5 0.5 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1
Initial R :
-------------------------------------------------
1.8 1.9 1.1 0.24
00.041 0.72 1.7
0 0 2 1.4
0 0 0 0.46
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
cublas init succeeded n_rows : 8, n_cols : 4 ||A -QR||_2 : 6.3e-07 ||Q^T Q - I||_2 : 3e-07 Error in col 0 - : 2, + : 0 Error in col 1 - : 2e-06, + : 2 Error in col 2 - : 1.5e-06, + : 2 Error in col 3 - : 1.5e-06, + : 2 ||Q_orig - Q||_2 : 0.0022
An dieser Stelle sind R und Q fertig :
Q_orig :
Matrix dims : 8 8
0.5 0.5 0.5 0.5 0 0 0 0
0.5 -0.5 0.5 -0.5 0 0 0 0
0.5 0.5 -0.5 -0.5 0 0 0 0
0.5 -0.5 -0.5 0.5 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1
Q :
Matrix dims : 8 8
-0.5 0.5 0.5 0.5 0 0 0 0
-0.5 -0.5 0.5 -0.5 0 0 0 0
-0.5 0.5 -0.5 -0.5 0 0 0 0
-0.5 -0.5 -0.5 0.5 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1
R :
-1.841 -1.909 -1.141 -0.2432
0 0.04108 0.7206 1.657
0 0 1.989 1.412
0 -1.863e-09 -2.384e-07 0.456
Q^TQ :
Matrix dims : 8 8
0 0 0 1.49e-08 0 0 0 0
0 -2.384e-07 0 -4.47e-08 0 0 0 0
0 0 -1.192e-07 -1.49e-08 0 0 0 0
1.49e-08 -4.47e-08 -1.49e-08 -1.192e-07 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
A :
0.9207 0.9752 1.926 1.884
0.9207 0.9341 1.205 -0.2288
0.9207 0.9752 -0.06383 0.01604
0.9207 0.9341 -0.7844 -1.185
QR :
0.9207 0.9752 1.926 1.884
0.9207 0.9341 1.205 -0.2288
0.9207 0.9752 -0.06383 0.01604
0.9207 0.9341 -0.7844 -1.185
Initial Q :
-------------------------------------------------
0.35 0.35 0.35 0.35 0.35 0.35 0.35 0.35
0.35-0.35 0.35-0.35 0.35-0.35 0.35-0.35
0.35 0.35-0.35-0.35 0.35 0.35-0.35-0.35
0.35-0.35-0.35 0.35 0.35-0.35-0.35 0.35
0.35 0.35 0.35 0.35-0.35-0.35-0.35-0.35
0.35-0.35 0.35-0.35-0.35 0.35-0.35 0.35
0.35 0.35-0.35-0.35-0.35-0.35 0.35 0.35
0.35-0.35-0.35 0.35-0.35 0.35 0.35-0.35
Initial R :
-------------------------------------------------
1.8 1.9 1.1 0.240.041 0.72 1.7 2
0 1.4 0.469.8e-06 0.46 1.4 2 1.7
0 0 0.710.039 0.25 1.1 1.9 1.8
0 0 0 0.99 0.150.094 0.87 1.8
0 0 0 0 2 1.3 0.340.012
0 0 0 0 0 0.6 1.6 2
0 0 0 0 0 0 1.5 0.57
0 0 0 0 0 0 00.0082
cublas init succeeded n_rows : 8, n_cols : 8 ||A -QR||_2 : 6.5e-06 ||Q^T Q - I||_2 : 1.3e-06 Error in col 0 - : 2, + : 3.4e-07 Error in col 1 - : 8.5e-07, + : 2 Error in col 2 - : 5.5e-07, + : 2 Error in col 3 - : 2, + : 3.4e-07 Error in col 4 - : 4.6e-07, + : 2 Error in col 5 - : 2, + : 8.4e-07 Error in col 6 - : 2, + : 8.8e-07 Error in col 7 - : 2, + : 6.5e-07 ||Q_orig - Q||_2 : 0.0022
An dieser Stelle sind R und Q fertig :
Q_orig :
Matrix dims : 8 8
0.3536 0.3536 0.3536 0.3536 0.3536 0.3536 0.3536 0.3536
0.3536 -0.3536 0.3536 -0.3536 0.3536 -0.3536 0.3536 -0.3536
0.3536 0.3536 -0.3536 -0.3536 0.3536 0.3536 -0.3536 -0.3536
0.3536 -0.3536 -0.3536 0.3536 0.3536 -0.3536 -0.3536 0.3536
0.3536 0.3536 0.3536 0.3536 -0.3536 -0.3536 -0.3536 -0.3536
0.3536 -0.3536 0.3536 -0.3536 -0.3536 0.3536 -0.3536 0.3536
0.3536 0.3536 -0.3536 -0.3536 -0.3536 -0.3536 0.3536 0.3536
0.3536 -0.3536 -0.3536 0.3536 -0.3536 0.3536 0.3536 -0.3536
Q :
Matrix dims : 8 8
-0.3536 0.3536 0.3536 -0.3536 0.3536 -0.3536 -0.3536 -0.3536
-0.3536 -0.3536 0.3536 0.3536 0.3536 0.3536 -0.3536 0.3536
-0.3536 0.3536 -0.3536 0.3536 0.3536 -0.3536 0.3536 0.3536
-0.3536 -0.3536 -0.3536 -0.3536 0.3536 0.3536 0.3536 -0.3536
-0.3536 0.3536 0.3536 -0.3536 -0.3536 0.3536 0.3536 0.3536
-0.3536 -0.3536 0.3536 0.3536 -0.3536 -0.3536 0.3536 -0.3536
-0.3536 0.3536 -0.3536 0.3536 -0.3536 0.3536 -0.3536 -0.3536
-0.3536 -0.3536 -0.3536 -0.3536 -0.3536 -0.3536 -0.3536 0.3536
R :
-1.841 -1.909 -1.141 -0.2432 -0.04108 -0.7206 -1.657 -1.989
2.384e-07 1.412 0.456 9.447e-06 0.4634 1.42 1.991 1.65
2.384e-07 5.96e-08 0.7121 0.0386 0.249 1.15 1.913 1.837
2.384e-07 -5.96e-08 -1.49e-07 -0.9911 -0.1538 -0.09442 -0.8676 -1.763
2.384e-07 5.96e-08 7.451e-08 7.451e-09 1.956 1.271 0.3364 0.01197
2.384e-07 -5.96e-08 4.47e-08 -5.96e-08 -1.788e-07 -0.596 -1.551 -2
2.384e-07 5.96e-08 -8.941e-08 -5.96e-08 -1.192e-07 2.98e-08 -1.529 -0.5718
2.384e-07 -5.96e-08 -1.49e-07 1.192e-07 -2.384e-07 -5.96e-08 1.192e-07 -0.008221
Q^TQ :
Matrix dims : 8 8
-5.364e-07 7.451e-08 1.118e-07 -1.118e-07 1.788e-07 -1.192e-07 -1.267e-07 -8.196e-08
7.451e-08 -5.96e-07 0 1.937e-07 3.725e-08 1.565e-07 -2.98e-08 1.788e-07
1.118e-07 0 -4.768e-07 6.706e-08 5.96e-08 1.49e-08 1.639e-07 1.192e-07
-1.118e-07 1.937e-07 6.706e-08 -4.172e-07 -1.49e-08 -1.043e-07 1.267e-07 -1.49e-07
1.788e-07 3.725e-08 5.96e-08 -1.49e-08 -1.192e-07 -2.98e-08 2.98e-08 7.451e-08
-1.192e-07 1.565e-07 1.49e-08 -1.043e-07 -2.98e-08 2.384e-07 -1.192e-07 -1.49e-08
-1.267e-07 -2.98e-08 1.639e-07 1.267e-07 2.98e-08 -1.192e-07 -1.788e-07 0
-8.196e-08 1.788e-07 1.192e-07 -1.49e-07 7.451e-08 -1.49e-08 0 -1.192e-07
A :
0.6511 1.174 0.8164 0.4501 1.012 1.857 3.481 3.476
0.6511 0.1758 0.494 -0.2508 0.576 0.3644 0.3626 -0.3575
0.6511 1.174 0.3129 -0.2781 0.7276 0.977 0.4334 0.5205
0.6511 0.1758 -0.00953 0.4228 0.5087 -0.3819 -1.458 -0.8084
0.6511 1.174 0.8164 0.4501 -0.3709 0.5368 1.065 1.643
0.6511 0.1758 0.494 -0.2508 -0.8073 -0.1128 0.1406 0.6497
0.6511 1.174 0.3129 -0.2781 -0.6557 -0.3431 0.1797 -0.4919
0.6511 0.1758 -0.00953 0.4228 -0.8747 -0.8591 0.4827 0.9958
QR :
0.6511 1.174 0.8164 0.4501 1.012 1.857 3.481 3.476
0.6511 0.1758 0.494 -0.2508 0.576 0.3644 0.3626 -0.3575
0.6511 1.174 0.3129 -0.2781 0.7276 0.977 0.4334 0.5205
0.6511 0.1758 -0.00953 0.4228 0.5087 -0.3819 -1.458 -0.8084
0.6511 1.174 0.8164 0.4501 -0.3709 0.5368 1.065 1.643
0.6511 0.1758 0.494 -0.2508 -0.8073 -0.1128 0.1406 0.6497
0.6511 1.174 0.3129 -0.2781 -0.6557 -0.3431 0.1797 -0.4919
0.6511 0.1758 -0.00953 0.4228 -0.8747 -0.8591 0.4827 0.9958
The plain program
(If you are looking at a locally installed CUDA HPC Praktikum version, then the program can be found at .. /.. /testsite / /step-4 /step-cu.cc . Otherwise, this is only the path on some remote server.)
#ifndef STEP_4_HH #define STEP_4_HH #include <cublas.h> #include <iostream> #include <fstream> #include <iostream> #include <vector> #include <numeric> #include <base/convergence_table.h> #include <base/parameter_handler.h> #include <lac/full_matrix.h> #include <QString> #include <QStringList> #include <QFile> #include <QTextStream> #include "cuda_driver_step-4.h" #include "cuda_driver_step-4.hh" #include <base/CUDATimer.h> #include <lac/MatrixCreator.h> #include <lac/blas++.h> #include <cmath>
struct GlobalData { int n_CUDA_devices; int current_device_id; cudaDeviceProp prop; void cublanc_gpu_info() { const int KB = 1024; const int MB = KB*KB; cudaGetDeviceProperties(&prop, this->current_device_id); printf("Currently used GPU: %s \n",prop.name); printf("Compute Capability: %d.%d \n",prop.major,prop.minor); printf("ClockRate: %uMHz \n",prop.clockRate/1000); printf("Warpsize: %d \n",prop.warpSize); printf("Number of Multiprocessors: %d \n",prop.multiProcessorCount); printf("Shared Memory: %uKB\n",prop.sharedMemPerBlock/KB); printf("Constant Memory: %uKB \n",prop.totalConstMem/KB); printf("Global Memory: %uMB \n",prop.totalGlobalMem/MB); printf("the device %s can concurrently copy memory " "between host and device while executing a kernel\n", (prop.deviceOverlap? "can": "cannot")); } }; GlobalData global_data;
template<typename T> struct PrecisionName { static std::string name(); }; template<> std::string PrecisionName<float>::name() { return "float"; } template<> std::string PrecisionName<double>::name() { return "double"; } template<typename T> std::string PrecisionName<T>::name() { return "unknown_T"; } namespace step4 {
struct TestUIParamsBase { TestUIParamsBase() {} static void declare(::ParameterHandler & prm); void get(::ParameterHandler & prm); int min_n_cols; int max_n_cols; double n_rows_growth_rate; int n_repetitions; template <typename T, typename blas> void save_results(const std::string test_name, const ::ConvergenceTable & results_table); private: TestUIParamsBase(const TestUIParamsBase & ) {} TestUIParamsBase & operator = (const TestUIParamsBase & / *other* /) { return *this; } }; } // namespace step4 END
void step4::TestUIParamsBase::declare(::ParameterHandler & prm) { prm.enter_subsection("Dimensions of test problems."); prm.declare_entry ("log2(min n cols)", "2", ::Patterns::Double(2,12), "Binary logarithm of minimal number of columns of " "upper triangular matrix R. " "Allowed range : [2,12]"); prm.declare_entry ("log2(max n cols)", "3", ::Patterns::Double(2,13), "Binary logarithm of minimal number of columns " "of upper triangular matrix R. " "Allowed range : [3,13]"); prm.declare_entry ("n rows growth rate", "1.2", ::Patterns::Double(1.1,10), "In each test instance the number of rows of R is " "increased by this factor. " "Allowed range : [1.1,10]"); prm.declare_entry("n repetitions", "1", ::Patterns::Integer(1), "Repeat the test for a given matrix size this many times."); prm.leave_subsection(); }
void step4::TestUIParamsBase::get(::ParameterHandler & prm) { prm.enter_subsection("Dimensions of test problems."); min_n_cols = pow(2., prm.get_double ("log2(min n cols)") ); max_n_cols = pow(2., prm.get_double ("log2(max n cols)") ); n_rows_growth_rate = prm.get_double("n rows growth rate"); n_repetitions = prm.get_integer("n repetitions"); prm.leave_subsection(); }
template <typename T, typename blas> void step4::TestUIParamsBase::save_results(const std::string test_name, const ::ConvergenceTable & results_table) { std::string filename(test_name); filename += ("_results_"); filename += blas::name(); filename += "_"; if (blas::name() == "cublas") { printf("Currently used GPU: %s \n", global_data.prop.name); filename += QString(global_data.prop.name).replace(" ", "_").toStdString().c_str(); filename += "_"; } filename += PrecisionName<T>::name(); filename += ".out"; std::ofstream out(filename.c_str()); out << "# max n_cols : " << this->max_n_cols << std::endl << "# min n_cols : " << this->min_n_cols << std::endl << "# growth rate : " << this->n_rows_growth_rate << std::endl << std::endl; results_table.write_text(out); } namespace step4 {
struct QRTestUIParams : public TestUIParamsBase { QRTestUIParams() : TestUIParamsBase() {} static void declare(::ParameterHandler & prm); void get(::ParameterHandler & prm); bool print_Q_orig; bool print_R_orig; bool print_A_orig; bool print_Q ; bool print_R; bool print_QR; bool print_QtQ; bool print_Q_col_errors; private: QRTestUIParams (const QRTestUIParams & / *other* /) : TestUIParamsBase() {} QRTestUIParams & operator = (const QRTestUIParams & / *other* /) { return *this; } }; } // namespace step4 END
void step4::QRTestUIParams::declare(::ParameterHandler & prm) { TestUIParamsBase::declare(prm); prm.enter_subsection("Visualization flags."); prm.declare_entry ("print original Q", "false", ::Patterns::Bool(), ""); prm.declare_entry ("print original R", "false", ::Patterns::Bool(), ""); prm.declare_entry ("print original A", "false", ::Patterns::Bool(), "The original A is given multiplying the original " "Q with the original R."); prm.declare_entry ("print Q from factorization", "false", ::Patterns::Bool(), ""); prm.declare_entry ("print R from factorization", "false", ::Patterns::Bool(), ""); prm.declare_entry ("print QR", "false", ::Patterns::Bool(), "Multiplying Q and R as obtained from the factorization " "should give something that closely resembles the original A"); prm.declare_entry ("print QtQ from factorization", "false", ::Patterns::Bool(), "Multiplying the Q obtained from the factorization with " "its own transpose should give a unit matrix."); prm.declare_entry ("print Q column errors", "false", ::Patterns::Bool(), "Computing ||Q_orig - Q||_2 must be done column-wise " "as the individual columns of Q are reproduced only " "up to a sign (the algorithm cannot distinguish " "the direction of a column vector)."); prm.leave_subsection(); }
void step4::QRTestUIParams::get(::ParameterHandler & prm) { this->TestUIParamsBase::get(prm); prm.enter_subsection("Visualization flags."); print_Q_orig = prm.get_bool ("print original Q"); print_R_orig = prm.get_bool ("print original R"); print_A_orig = prm.get_bool ("print original A"); print_Q = prm.get_bool ("print Q from factorization"); print_R = prm.get_bool ("print R from factorization"); print_QR = prm.get_bool ("print QR"); print_QtQ = prm.get_bool ("print QtQ from factorization"); print_Q_col_errors = prm.get_bool ("print Q column errors"); prm.leave_subsection(); } namespace step4 {
template <typename T, typename blas> class QRTest { public: typedef typename blas_pp<T, blas>::FullMatrixAccessor FullMatrixAccessor; typedef typename blas_pp<T, blas>::Matrix Matrix; typedef transpose<Matrix> tr; typedef typename blas_pp<T, blas>::SubMatrix SubMatrix; typedef typename blas_pp<T, blas>::MatrixSubCol MatrixSubCol; typedef typename blas_pp<T, blas>::Vector Vector; QRTest(::ParameterHandler & prm); void run(); protected: void check_results(const ::FullMatrix<T> & A, const step4::CudaQRDecomposition<T, blas>& QRf, T elapsed_time); private: void setup_and_assemble(unsigned int nr, unsigned int nc); void factorize(); void save_results(); ::FullMatrix<T> Q, R, H; QRTestUIParams params; ::ConvergenceTable results_table; }; } // namespace step4 END
template <typename T, typename blas> step4::QRTest<T, blas>::QRTest(::ParameterHandler & prm) { params.get(prm); }
template <typename T, typename blas> void step4::QRTest<T, blas>::run() { for (int nc = this->params.min_n_cols; nc < this->params.max_n_cols; nc*=2) for (int nr = nc; nr <= this->params.max_n_cols; nr=std::max(nr+1, int(nr*this->params.n_rows_growth_rate) ) ) { setup_and_assemble(nr, nc); factorize(); } setup_and_assemble(this->params.max_n_cols, this->params.max_n_cols); factorize(); save_results(); }
template <typename T, typename blas> void step4::QRTest<T, blas>::setup_and_assemble(unsigned int nr, unsigned int nc) { Assert(nr >= nc, ::ExcMessage("n_cols must not exceed n_rows.")); int log2_nc = std::log(nc)/std::log(2); MatrixCreator::hadamard(log2_nc, this->H); this->H /= std::sqrt(this->H.n_rows() ); this->Q.reinit(nr, nr); for (unsigned int r = 0; r < nc; ++r) for (unsigned int c = 0; c < nc; ++c) Q(r,c) = H(r,c); for (unsigned int r = nc; r < nr; ++r) Q(r,r) = 1; this->R.reinit(nr, nc); int tmp = 1; for (unsigned int r = 0; r < nr; ++r) for (unsigned int c = r; c < nc; ++c) R(r,c) = 1+std::sin(tmp++); if (this->params.print_Q_orig) { std::cout << "Initial Q (Hadamard-Matrix, siehe wikipedia): \n"; std::cout << "----------------------------------------------" << std::endl; Q.print(std::cout); } if (this->params.print_R_orig) { std::cout << "\nInitial R : \n"; std::cout << "----------------------------------------------" << std::endl; R.print(std::cout, 12, 5); } if (this->params.print_Q_orig || this->params.print_R_orig) std::cout << std::endl; }
template <typename T, typename blas> void step4::QRTest<T, blas>::factorize() { ::FullMatrix<T> A(R.n_rows(), R.n_cols() ); ::FullMatrix<T> Q_orig(Q); Q_orig.mmult(A, R); step4::CudaQRDecomposition<T, blas> QR; T elapsed_time = QR.householder(A); check_results(A, QR, elapsed_time); }
template <typename T, typename blas> void step4::QRTest<T, blas>::check_results(const ::FullMatrix<T> & A, const step4::CudaQRDecomposition<T, blas>& QRf, T elapsed_time) { int n_rows = QRf.R().n_rows(); int n_cols = QRf.R().n_cols(); std::cout << "n_rows : " << n_rows << ", n_cols : " << n_cols << std::endl; FullMatrixAccessor A_t_ugly(A, true / *column-major copy* /); Matrix A_backup; A_backup = A_t_ugly; const SubMatrix Q_num(const_cast<Matrix&>(QRf.Q()), 0, 0); const SubMatrix R_num(const_cast<Matrix&>(QRf.R()), 0, 0); Matrix QR(QRf.Q().n_rows(), QRf.R().n_cols()); SubMatrix QR_num(QR, 0, 0); QR_num = Q_num * R_num; Matrix QtQ = tr(QRf.Q()) * QRf.Q(); Matrix A_m_QR; A_m_QR = A_backup; A_m_QR -= QR; T l2_A_QR_error = A_m_QR.l2_norm(); std::cout << "||A -QR||_2 : " << l2_A_QR_error << std::endl; Matrix I; ::IdentityMatrix I_h(n_rows); I = I_h; QtQ -= I; T l2_QtQ_error = QtQ.l2_norm(); std::cout << "||Q^T Q - I||_2 : " << l2_QtQ_error << std::endl; FullMatrixAccessor Q_t_ugly(Q, true / *column-major copy* /); Matrix Q_orig; Q_orig = Q_t_ugly; T l2_Q_error = 0; for (int c = 0; c < n_cols; ++c) { MatrixSubCol Q_col(const_cast<Matrix&>(QRf.Q()),0,c); MatrixSubCol Q_orig_col(Q_orig,0,c); Q_orig_col -= Q_col; T c_m_err = Q_orig_col.l2_norm(); Q_orig_col += Q_col; Q_orig_col += Q_col; T c_p_err = Q_orig_col.l2_norm(); l2_Q_error += std::min(c_m_err, c_p_err); if (this->params.print_Q_col_errors) std::cout << "Error in col " << c << " - : " << c_m_err << ", + : " << c_p_err << std::endl; } l2_Q_error = std::sqrt(l2_Q_error); std::cout << "||Q_orig - Q||_2 : " << l2_Q_error << std::endl; this->results_table.add_value("n_rows", n_rows); this->results_table.add_value("n_cols", n_cols); this->results_table.add_value("||A -QR||_2", double(l2_A_QR_error) ); this->results_table.set_precision ("||A -QR||_2", 16); this->results_table.add_value("||Q^T Q - I||_2", double(l2_QtQ_error) ); this->results_table.set_precision ("||Q^T Q - I||_2", 16); this->results_table.add_value("||Q - Q_orig||_2", double(l2_Q_error) ); this->results_table.set_precision ("||Q - Q_orig||_2", 16); this->results_table.add_value("elapsed time", double(elapsed_time) ); this->results_table.set_precision ("elapsed time", 16); if (this->params.print_Q_orig || this->params.print_R_orig) std::cout << "\nAt this point R and Q are done :" << std::endl; if (this->params.print_Q_orig) { Q_orig = Q_t_ugly; std::cout << "\nQ_orig :" << std::endl; Q_orig.print(); } if (this->params.print_Q) { std::cout << "\nQ_num :" << std::endl; QRf.Q().print(); } if (this->params.print_R) { SubMatrix R_upper_square(const_cast<Matrix&>(QRf.R()), 0, n_cols, 0, n_cols); std::cout << "\nR :" << std::endl; R_upper_square.print(); } if (this->params.print_QtQ) { std::cout << "\nQ^TQ :" << std::endl; QtQ.print(); } if (this->params.print_A_orig) { SubMatrix A_upper_square(A_backup, 0, n_rows, 0, n_cols); std::cout << "\nA_orig :" << std::endl; A_upper_square.print(); } if (this->params.print_QR) { SubMatrix QR_upper_square(QR, 0, n_rows, 0, n_cols); std::cout << "\nQ_num * R_num :" << std::endl; QR_upper_square.print(); } }
template <typename T, typename blas> void step4::QRTest<T, blas>::save_results() { this->params.template save_results<T, blas>(std::string("QRTest"), results_table); } namespace step4 {
struct SimUIParams { SimUIParams() {} static void declare(::ParameterHandler & prm); void get(::ParameterHandler & prm); bool run_cublas_float, run_cublas_double; bool run_cpu_blas_float, run_cpu_blas_double; }; } // namespace step4 END
void step4::SimUIParams::declare(::ParameterHandler & prm) { prm.enter_subsection("Global parameters"); prm.declare_entry("Run cublas float", "false", ::Patterns::Bool(), "Single precision is offered by any CUDA-capable GPU."); prm.declare_entry("Run cublas double", "false", ::Patterns::Bool(), "Only available on graphics cards of compute capability " "1.3 and higher"); prm.declare_entry("Run CPU-BLAS float", "false", ::Patterns::Bool(), "Depending on the platform this is either the reference " "BLAS from www.netlib.org or a tuned vendor-specific " "version. For instance Intel's MKL, the Accelerate " "framework by Apple or AMDs ACML."); prm.declare_entry("Run CPU-BLAS double", "false", ::Patterns::Bool(), "Cf. test for floats"); prm.leave_subsection(); }
void step4::SimUIParams::get(::ParameterHandler & prm) { prm.enter_subsection("Global parameters"); run_cublas_float = prm.get_bool("Run cublas float"); run_cublas_double = prm.get_bool("Run cublas double"); run_cpu_blas_float = prm.get_bool("Run CPU-BLAS float"); run_cpu_blas_double = prm.get_bool("Run CPU-BLAS double"); prm.leave_subsection(); } namespace step4 {
void run_qr_tests(int / *argc* /, char *argv[]) { ::ParameterHandler prm_handler; SimUIParams::declare(prm_handler); QRTestUIParams::declare(prm_handler); std::string prm_filename(argv[0]); prm_filename += "-QR.prm"; prm_handler.read_input (prm_filename); prm_filename += ".log"; std::ofstream log_out_text(prm_filename.c_str()); prm_handler.print_parameters (log_out_text, ::ParameterHandler::Text); SimUIParams params; params.get(prm_handler); for(int DevNo = 0; DevNo < global_data.n_CUDA_devices; DevNo++) { cudaSetDevice(DevNo); global_data.current_device_id = DevNo; global_data.cublanc_gpu_info(); if (params.run_cublas_float) { std::cout << "Householder-QR<float> using cublas :\n" << "------------------------------------------------" << std::endl; QRTest<float, cublas> cublas_qr_test_float(prm_handler); cublas_qr_test_float.run(); std::cout << "\nHouseholder-QR<float> using cublas DONE \n" << "------------------------------------------------\n" << std::endl; } #ifdef CUDA_DOUBLE_CAPABLE if (params.run_cublas_double) { std::cout << "\nHouseholder-QR<double> using cublas :\n" << "------------------------------------------------" << std::endl; QRTest<double, cublas> cublas_qr_test_double(prm_handler); cublas_qr_test_double.run(); std::cout << "\nHouseholder-QR<double> using cublas DONE \n" << "------------------------------------------------\n" << std::endl; } #endif } if (params.run_cpu_blas_float) { std::cout << "\nHouseholder-QR<float> using ATLAS/CBLAS :\n" << "------------------------------------------------" << std::endl; QRTest<float, blas> blas_qr_test_float(prm_handler); blas_qr_test_float.run(); std::cout << "\nHouseholder-QR<float> using ATLAS/CBLAS DONE \n" << "------------------------------------------------\n" << std::endl; } if (params.run_cpu_blas_double) { std::cout << "\nHouseholder-QR<double> using ATLAS/CBLAS :\n" << "------------------------------------------------" << std::endl; QRTest<double, blas> blas_qr_test_double(prm_handler); blas_qr_test_double.run(); std::cout << "\nHouseholder-QR<double> using ATLAS/CBLAS DONE \n" << "------------------------------------------------\n" << std::endl; } } } // namespace step4 END #endif // STEP_4_HH #ifndef CUDADriver_STEP_4_H #define CUDADriver_STEP_4_H #include <lac/full_matrix.h> #include <lac/blas++.h> #include <lac/cublas_algorithms.h> #include "cuda_kernel_wrapper_step-4.cu.h" namespace step4 {
template <typename T, typename blas> class CudaQRDecomposition { public: typedef blas_pp<T, blas> BLAS; typedef typename BLAS::blas_wrapper_type BW; typedef typename BLAS::FullMatrixAccessor FullMatrixAccessor; typedef typename BLAS::Matrix Matrix; typedef typename BLAS::SubMatrix SubMatrix; typedef typename BLAS::MatrixSubCol MatrixSubCol; typedef typename BLAS::Vector Vector; typedef typename BLAS::SubColVector SubColVector; typedef typename BLAS::SubVectorBase SubVectorBase; CudaQRDecomposition(); ~CudaQRDecomposition (); T householder (const ::FullMatrix<T>& A); T lapack_based(const ::FullMatrix<T> &A); const Matrix & Q() const { return Q_d; } const Matrix & R() const { return R_d; } private: Matrix Q_d, R_d; void check_matrix_dimensions(const ::FullMatrix<T>& A); }; } // namespace step4 END #endif // CUDADriver_STEP_4_H #ifndef CUDA_DRIVER_STEP_4_HH #define CUDA_DRIVER_STEP_4_HH #include "cuda_driver_step-4.h" #include "cuda_kernel_wrapper_step-4.cu.h" #include <cutil_inline.h> #include <iomanip> #include <cmath> #include <QtGlobal> #include <base/sign.h> #include <base/CUDATimer.h> #include <lac/expression_template.h> #include <lac/FullMatrixAccessor.h> #include <lac/cublas_algorithms.h>
template <typename T, typename blas> step4::CudaQRDecomposition<T, blas>::CudaQRDecomposition() { BW::Init(); }
template <typename T, typename blas> step4::CudaQRDecomposition<T, blas>::~CudaQRDecomposition() { BW::Shutdown(); }
template <typename T, typename blas> void step4::CudaQRDecomposition<T, blas>::check_matrix_dimensions(const ::FullMatrix<T>& A) { const bool is_matrix_dim_correct = A.n_rows() >= A.n_cols(); #ifdef QT_NO_DEBUG AssertThrow(is_matrix_dim_correct, ::ExcMessage("n_rows must be greater n_cols") ); #else Assert(is_matrix_dim_correct, ::ExcMessage("n_rows must be greater n_cols") ); #endif }
template <typename T, typename blas> T step4::CudaQRDecomposition<T, blas>::householder(const ::FullMatrix<T> &A) { check_matrix_dimensions(A); int n_rows = A.n_rows(); int n_cols = A.n_cols(); ::FullMatrixAccessor<T> A_t_ugly(A, true / * transpose copy* /); this->R_d = A_t_ugly; ::IdentityMatrix eye_image(n_rows); Q_d = eye_image; T alpha = 0, sigma = 0; Vector x(n_rows); Vector u(n_rows); Vector k(n_rows); SubMatrix A_rest(R_d, 0, 0); transpose<SubMatrix> A_rest_T (A_rest); SubMatrix Q_0c(Q_d, 0, 0); CUDATimer timer; for(int c=0; c<n_cols-1; c++) { A_rest.reset(c, n_rows, c, n_cols); Q_0c.reset(0, n_rows, c, n_rows); T A_tt1 = R_d(c, c); MatrixSubCol sub_col_A(R_d, c, c); { alpha = sign(A_tt1) * sub_col_A.l2_norm(); T beta_t = A_tt1 + alpha; if (std::fabs(alpha) < 1e-14) continue; sigma = beta_t/alpha; u = sub_col_A; // std::cout << "u :\n"; u.print(); u.add(c, alpha); // std::cout << "u("<<c<<") + alpha :\n"; u.print(); Assert(std::fabs(beta_t) > 1e-14, ::ExcMessage("Div by 0!") ); u *= 1./beta_t; } x = A_rest_T * u; A_rest.add_scaled_outer_product(-sigma, u, x); k = Q_0c * u; Q_0c.add_scaled_outer_product(-sigma, k, u); } timer.print_elapsed("Time spent on Householder-QR excluding host-device memory traffic : "); return timer.elapsed(); }
template <typename T, typename blas> T step4::CudaQRDecomposition<T, blas>::lapack_based(const ::FullMatrix<T> &A) { #ifdef USE_LAPACK FullMatrixAccessor A_t_ugly(A, true / *transpose while copying* /); __CLPK_integer m = A_t_ugly.n_rows(); __CLPK_integer n = A_t_ugly.n_cols(); __CLPK_integer lda = A_t_ugly.n_rows(); __CLPK_integer lwork = -1; __CLPK_integer info; std::vector<float> tau(std::min(A_t_ugly.n_rows(), A_t_ugly.n_cols())); std::vector<float> work(1); float * A_val = const_cast<float*>(A_t_ugly.val()); sgeqrf_(&m, &n, A_val, &lda, &tau[0], &work[0], &lwork, &info); if (info != 0) { printf("sgeqrf failed with error code %d\n", (int)info); return 0; } lwork = work[0]; work.resize(lwork); sgeqrf_(&m, &n, A_val, &lda, &tau[0], &work[0], &lwork, &info); if (info != 0) { printf("sgeqrf failed with error code %d\n", (int)info); return 0; } this->R_d = A_t_ugly; #endif } #endif // CUDA_DRIVER_STEP_4_HH #ifndef CUDA_KERNEL_STEP_4_CU_H #define CUDA_KERNEL_STEP_4_CU_H
#endif // CUDA_KERNEL_STEP_4_CU_H #include <cutil_inline.h> #include <cuda_kernel_wrapper_step-4.cu.h>
#include "step-4.hh"
int main(int argc, char *argv[]) { cudaGetDeviceCount(&global_data.n_CUDA_devices); std::cout << "N available CUDA devices : " << global_data.n_CUDA_devices << std::endl; step4::run_qr_tests(argc, argv); std::cout << std::endl; }
documentation generated on Mon Jul 18 12:05:10 2011 by
doxygen
1.5.7