|
This project in progress is in collaboration with the INRIA group in Pau and Bordeaux. They developped a finite element code Montjoie that can solve multiple PDEs. In particular, it can solve a scalar acoustic wave equation in the frequency domain. The goal is to use this code in order to obtain travel time sensitivity kernels in spherical geometries but also to use it as forward solver in order to solve a nonlinear inverse problem. This corresponds to the classical topic of parameter identification in PDEs. However, due to the strongly varying coefficient in the Sun (and particularly close to the surface), this problem is extremely challenging in term of forward problem (one of the problem concerns the choice of the boundary conditions) and for the inverse problem.
This work is presented in the paper "Computational helioseismology in the frequency domain: acoustic waves in axisymmetric solar models with flows", accepted for publication in Astronomy & Astrophysics.
|
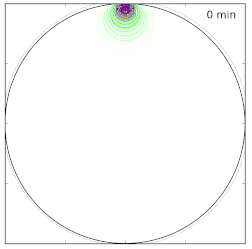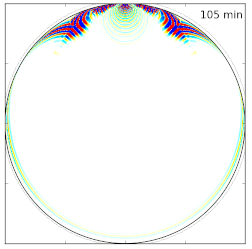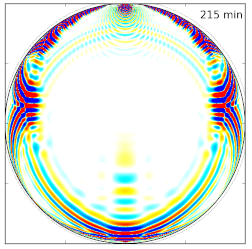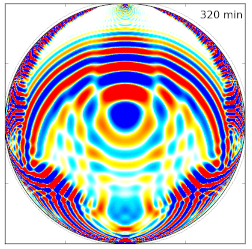
Green's function in the time domain
(solution of a scalar acoustic wave equation).
This quantity is the basis ingredient to compute sensitivity kernels.
|

