Parallel Magnetic Resonance imaging (MRI)¶
Standard MRI is described by the Fourier transform \(\mathcal{F}\) as forward operator (here in two dimensions). To accelerate data acquisition, parallel MRI uses simultaneous measurements by \(N\) receiver coils. This allows undersampling of the Fourier domain leading to speed-ups. Parallel MRI is described by the forward operator
Here \(\rho\) describes the hydrogen density and is the main quantity of interest. To take into account effects such as motion artifacts, \(\rho\) has to be modeled as a complex-valued function. \(c_1,\dots, c_N\) describe complex-valued coil profile, which may be assumed to be smooth. As they depend on the sample \(\rho\), they must be reconstructed together with \(\rho\). \(M\) is a 0-1-mask describing the undersampling pattern.
[1]:
import matplotlib.pyplot as plt
import matplotlib as mplib
from matplotlib.colors import hsv_to_rgb
import numpy as np
from scipy.io import loadmat
Defining the operators¶
We define a general Coil Multiplier that that Multiplies the complex coil profiles with the hydrogen density. Which can then be used to define the parallel MRI as using the composition with a Fourier transform in the non-stacked directions.
[2]:
from regpy.vecsps import UniformGridFcts
from regpy.operators import Operator, FourierTransform, DirectSum, PtwMultiplication
[3]:
class CoilMult(Operator):
"""Operator that implements the multiplication between density and coil profiles. The domain
is a direct sum of the `grid` (for the densitiy) and a `regpy.vecsps.UniformGridFcts` of `ncoils`
copies of `grid`, stacked along the 0th dimension.
Parameters
----------
grid : regpy.vecsps.UniformGridFcts
The grid on which the density is defined.
ncoils : int
The number of coils.
"""
def __init__(self, grid, ncoils):
assert isinstance(grid, UniformGridFcts)
assert grid.ndim == 2
self.grid = grid
"""The density grid."""
if(ncoils>1):
self.coilgrid = UniformGridFcts(ncoils, *grid.axes, dtype=grid.dtype)
else:
self.coilgrid=UniformGridFcts(*grid.axes, dtype=grid.dtype)
"""The coil grid, a stack of copies of `grid`."""
self.ncoils = ncoils
"""The number of coils."""
super().__init__(
domain=self.grid + self.coilgrid,
codomain=self.coilgrid
)
def _eval(self, x, differentiate=False, adjoint_derivative=False):
density, coils = self.domain.split(x)
if differentiate or adjoint_derivative:
r"""We need to copy here since `.split()` returns views into `x` if possible."""
self._density = density.copy()
self._coils = coils.copy()
return density * coils
def _derivative(self, x):
density, coils = self.domain.split(x)
return density * self._coils + self._density * coils
def _adjoint(self, y):
density = self._density
coils = self._coils
if self.grid.is_complex:
r"""Only `conj()` in complex case. For real case, we can avoid the copy."""
density = np.conj(density)
coils = np.conj(coils)
if(self.ncoils>1):
return self.domain.join(
np.sum(coils * y, axis=0),
density * y)
return self.domain.join(coils*y,density*y)
def parallel_mri(grid, ncoils, centered=False):
"""Construct a parallel MRI operator by composing a `regpy.operators.FourierTransform` and a
`CoilMult`. Subsampling patterns need to added by composing with e.g. a `cartesian_sampling`.
Parameters
----------
grid : vecsps.UniformGridFcts
The grid on which the density is defined.
ncoils : int
The number of coils.
centered : bool
Whether to use a centered FFT. If true, the operator will use fftshift.
Returns
-------
Operator
"""
cmult = CoilMult(grid, ncoils)
ft = FourierTransform(cmult.codomain, axes=range(1, cmult.codomain.ndim), centered=centered)
return ft * cmult
Partial Sobolev initialization¶
Partial reimplementation of the Sobolev Gram matrix. Can be composed with forward operator (from the right) to substitute coils = ifft(aux / sqrt(sobolev_weights)), making aux the new unknown. This can be used to avoid the numerically unstable Gram matrix for high Sobolev indices.
[4]:
def sobolev_smoother(codomain, sobolev_index, factor=None, centered=False):
"""
Parameters
----------
codomain :
Codomain of the operator
sobolev_index : int
centered : bool
Whether to use a centered FFT. If true, the operator will use fftshift.
factor : float
If factor is None (default): Implicit scaling based on the codomain. Otherwise,
the coordinates are normalized and this factor is applied.
"""
grid, coilsgrid = codomain
ft = FourierTransform(coilsgrid, axes=(1, 2), centered=centered)
ft_codomain_coord_slice=np.asarray(ft.codomain.coords[1:])
if factor is None:
mulfactor = grid.volume_elem * (
1 + np.linalg.norm(ft_codomain_coord_slice, axis=0)**2
)**(-sobolev_index / 2)
else:
mulfactor = ( 1 + factor * np.linalg.norm(ft_codomain_coord_slice/2./np.amax(np.abs(ft_codomain_coord_slice)), axis=0)**2
)**(-sobolev_index / 2)
mul = PtwMultiplication(ft.codomain, mulfactor)
return DirectSum(grid.identity, ft.inverse * mul, codomain=codomain)
Estimating the Sampling pattern¶
Estimate the sampling pattern from measured data is very important. Here we have a short method, that if some measurement point is zero in all coil profiles it is assumed to be outside of the sampling pattern. This method has a very low probability of failing, especially non-integer data.
[5]:
def estimate_sampling_pattern(data):
return np.all(data != 0, axis=0)
Complex to rgb conversion¶
To plot the complex coil profiles we need to convert the complex arrays to rgb. The following method converts array of complex numbers into array of RGB color values for plotting. The hue corresponds to the argument. The brightness corresponds to the absolute value.
Parameters >z : numpy.ndarray >array of complex numbers
Returns > numpy.ndarray > Array that contains three values for each value in z containing the RGB representation of this value.
[6]:
def complex_to_rgb(z):
HSV = np.dstack( (np.mod(np.angle(z)/(2.*np.pi),1), 1.0*np.ones(z.shape), np.abs(z)/np.max((np.abs(z[:]))), ))
return hsv_to_rgb(HSV)
Load data from file and estimate sampling pattern¶
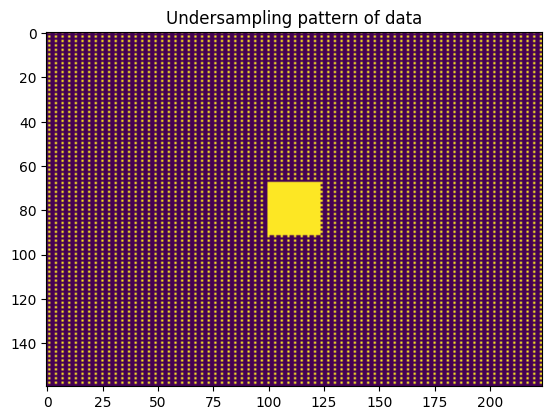
Here we load the data from a stored file normalize it and extract the number of coils, and shape. Using this information we can define the space for each coil profile as a uniform grid of complex valued functions. Finally, we use the data to extract the mask of the sampling pattern and we plot that sampling pattern.
[7]:
data = loadmat('../../../../examples/mri/data/ksp3x2.mat')['Y']
data = np.transpose(data,(2,0,1))*(100/np.linalg.norm(data))
# normalize and transpose data
nrcoils,n1,n2 = data.shape
grid = UniformGridFcts((-1, 1, n1), (-1, 1, n2), dtype=complex)
mask = estimate_sampling_pattern(data)
plt.imshow(mask.T); plt.title('Undersampling pattern of data')
[7]:
Text(0.5, 1.0, 'Undersampling pattern of data')
Set up forward operator¶
With the defined coil grid and number of coils we can now define out mri operator. First we have the full operator which does not know the sampling pattern. Then we define the point wise multiplication using the mask from the sampling pattern and then we add the Sobolev smoother which allows us to include the Sobolev smoothing already into the operator rather then latter in the setting and solver. Then we only need to compose these operators to get our final parallel MRI operator.
[8]:
sobolev_index = 32
full_mri_op = parallel_mri(grid=grid, ncoils=nrcoils,centered=True)
sampling = PtwMultiplication(full_mri_op.codomain,(1.+0j)* mask)
smoother = sobolev_smoother(full_mri_op.domain, sobolev_index, factor=220.)
parallel_mri_op = sampling * full_mri_op * smoother
Set up initial guess¶
As an initial guess we use constant density and zero coil profiles. First we split the composed zero vector and then we set the density to constant one. Note we use init_density[...] = 1 to have a mutable operation on the variable.
[9]:
init = parallel_mri_op.domain.zeros()
init_density, _ = parallel_mri_op.domain.split(init)
init_density[...] = 1
Set up regularization method¶
Having defined the operator and the data and initial guess we can now first define a setting. Then we define the solver and a stop rule. Here we will stop after 5 iterations and use an iterative regularized Gauss Newton method as solver.
[10]:
from regpy.stoprules import CountIterations
from regpy.solvers import Setting
from regpy.solvers.nonlinear.irgnm import IrgnmCG
from regpy.hilbert import L2
[11]:
setting = Setting(op=parallel_mri_op, penalty=L2, data_fid=L2, data = data, regpar=1.)
solver = IrgnmCG(
setting=setting,
regpar_step=1/3.,
init=init
)
stoprule = CountIterations(max_iterations=5)
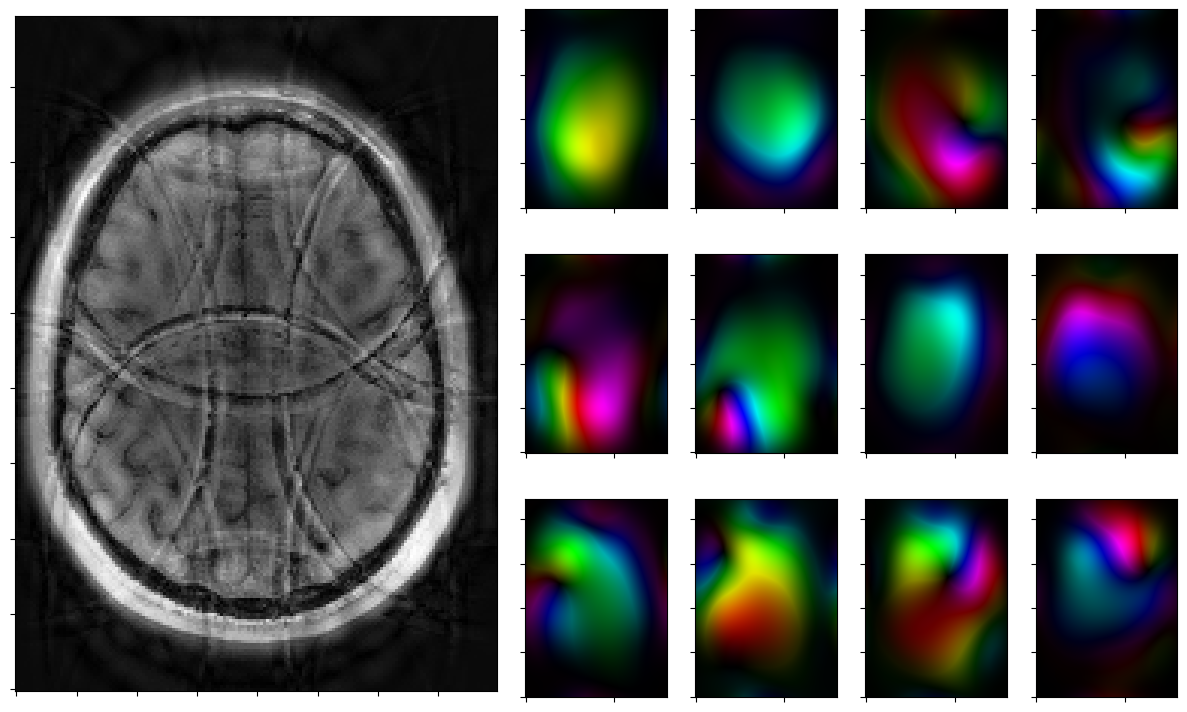
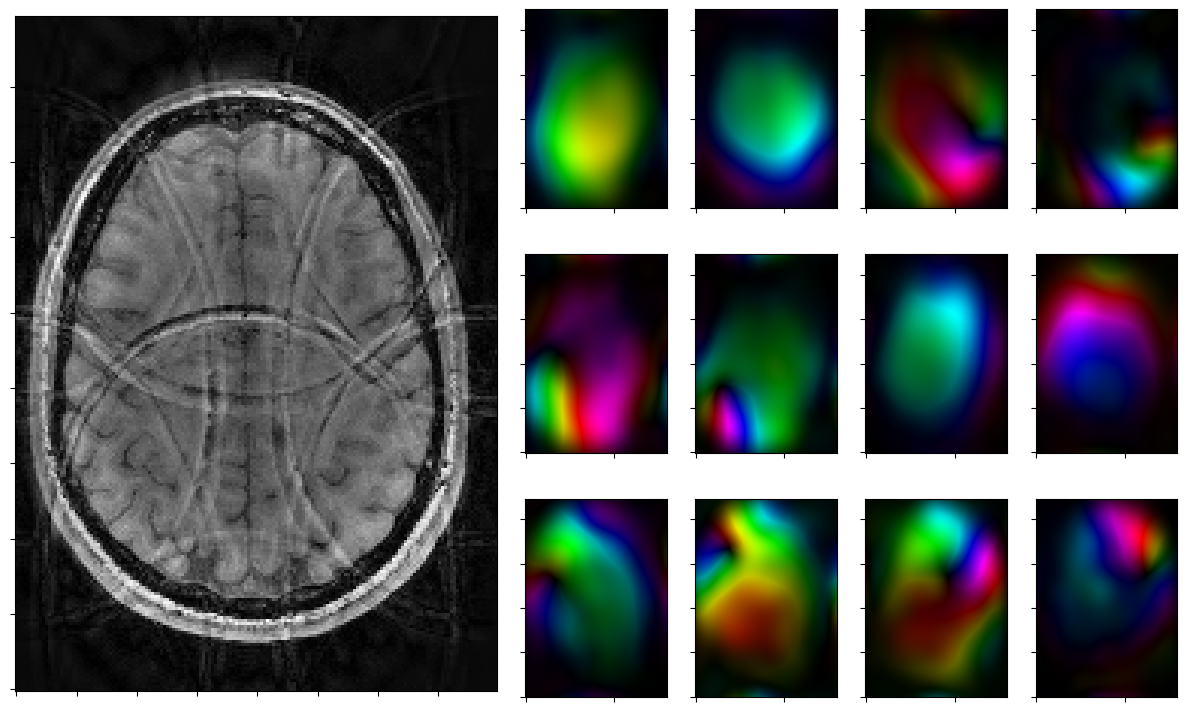
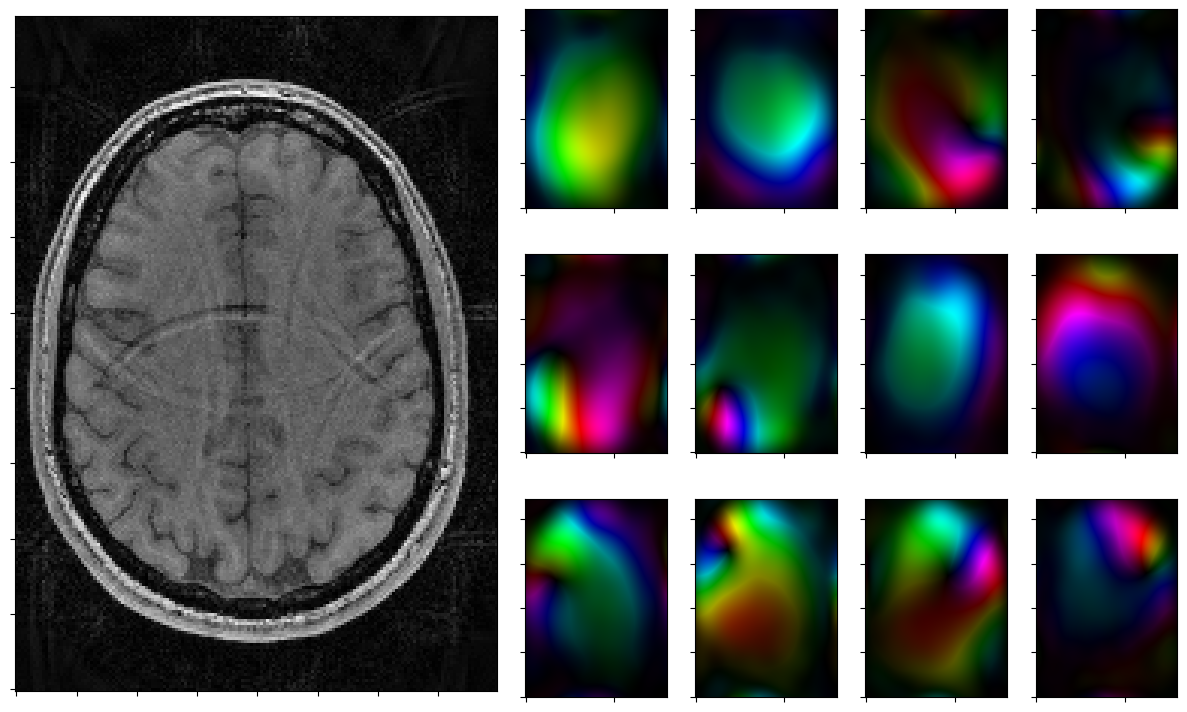
Run solver by hand and plot iterates¶
Run the solver iteratively and plot each step.
[12]:
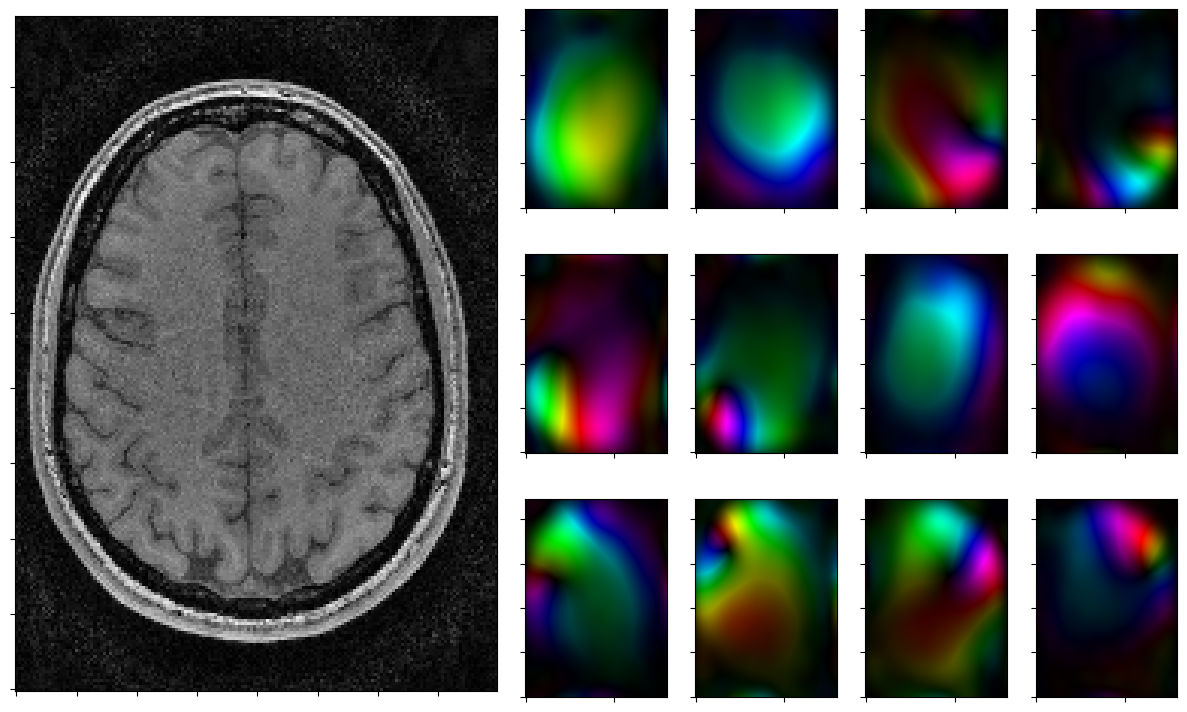
for reco, reco_data in solver.while_(stoprule):
rho, coils = smoother.codomain.split(smoother(reco))
#rho, coils = normalize(rho,coils)
fig = plt.figure(figsize = (15,9))
gs = fig.add_gridspec(3,7)
axs = [fig.add_subplot(gs[0:3, 0:3])]
axs[0].imshow(np.abs(rho),cmap=mplib.colormaps['Greys_r'],origin='lower')
axs[0].xaxis.set_ticklabels([])
axs[0].yaxis.set_ticklabels([])
for j in range(3):
for k in range(3,7):
axs.append(fig.add_subplot(gs[j,k]))
axs[-1].xaxis.set_ticklabels([])
axs[-1].yaxis.set_ticklabels([])
for j in range(nrcoils):
axs[1+j].imshow(complex_to_rgb(coils[j,:,:]),origin='lower')
plt.show()
2026-01-29 15:10:07,969 INFO CountIterations :: it. 0>=5
2026-01-29 15:10:08,235 INFO CombineRules :: it. 0>=1000 | ((rel X:--(x=0)! | rel Y:--(y=0) ) & kappa:1.0e+00) | it. 0>=1000
2026-01-29 15:10:08,480 INFO CombineRules :: it. 1>=1000 | ((rel X:4.5e-02>=2.5e-01 | rel Y:1.0e-01>=2.5e-01 [Rule RelTolXStop(0.3333333333333333) triggered.Rule RelTolYStop(0.3333333333333333) triggered.]) & kappa:1.0e+00[All rules triggered.]) | it. 1>=1000

2026-01-29 15:10:09,152 INFO CountIterations :: it. 1>=5
2026-01-29 15:10:09,309 INFO CombineRules :: it. 0>=1000 | ((rel X:--(x=0)! | rel Y:--(y=0) ) & kappa:1.0e+00) | it. 0>=1000
2026-01-29 15:10:09,478 INFO CombineRules :: it. 1>=1000 | ((rel X:3.2e+01>=2.5e-01 | rel Y:3.1e+00>=2.5e-01 ) & kappa:1.1e+00) | it. 1>=1000
2026-01-29 15:10:09,618 INFO CombineRules :: it. 2>=1000 | ((rel X:1.2e+01>=2.5e-01 | rel Y:1.5e+00>=2.5e-01 ) & kappa:1.3e+00) | it. 2>=1000
2026-01-29 15:10:09,868 INFO CombineRules :: it. 3>=1000 | ((rel X:7.0e+00>=2.5e-01 | rel Y:9.3e-01>=2.5e-01 ) & kappa:1.7e+00) | it. 3>=1000
2026-01-29 15:10:10,029 INFO CombineRules :: it. 4>=1000 | ((rel X:4.6e+00>=2.5e-01 | rel Y:6.8e-01>=2.5e-01 ) & kappa:2.2e+00) | it. 4>=1000
2026-01-29 15:10:10,224 INFO CombineRules :: it. 5>=1000 | ((rel X:3.1e+00>=2.5e-01 | rel Y:5.0e-01>=2.5e-01 ) & kappa:2.2e+00) | it. 5>=1000
2026-01-29 15:10:10,380 INFO CombineRules :: it. 6>=1000 | ((rel X:2.2e+00>=2.5e-01 | rel Y:3.7e-01>=2.5e-01 ) & kappa:2.3e+00) | it. 6>=1000
2026-01-29 15:10:10,539 INFO CombineRules :: it. 7>=1000 | ((rel X:1.6e+00>=2.5e-01 | rel Y:3.0e-01>=2.5e-01 ) & kappa:2.8e+00) | it. 7>=1000
2026-01-29 15:10:10,695 INFO CombineRules :: it. 8>=1000 | ((rel X:1.3e+00>=2.5e-01 | rel Y:2.5e-01>=2.5e-01 ) & kappa:3.6e+00) | it. 8>=1000
2026-01-29 15:10:10,893 INFO CombineRules :: it. 9>=1000 | ((rel X:1.1e+00>=2.5e-01 | rel Y:2.2e-01>=2.5e-01 [Rule RelTolYStop(0.3333333333333333) triggered.]) & kappa:4.6e+00[All rules triggered.]) | it. 9>=1000
2026-01-29 15:10:11,564 INFO CountIterations :: it. 2>=5
2026-01-29 15:10:11,729 INFO CombineRules :: it. 0>=1000 | ((rel X:--(x=0)! | rel Y:--(y=0) ) & kappa:1.0e+00) | it. 0>=1000
2026-01-29 15:10:11,909 INFO CombineRules :: it. 1>=1000 | ((rel X:3.6e+01>=2.5e-01 | rel Y:2.5e+00>=2.5e-01 ) & kappa:1.0e+00) | it. 1>=1000
2026-01-29 15:10:12,064 INFO CombineRules :: it. 2>=1000 | ((rel X:1.6e+01>=2.5e-01 | rel Y:1.2e+00>=2.5e-01 ) & kappa:1.3e+00) | it. 2>=1000
2026-01-29 15:10:12,228 INFO CombineRules :: it. 3>=1000 | ((rel X:8.8e+00>=2.5e-01 | rel Y:7.0e-01>=2.5e-01 ) & kappa:1.6e+00) | it. 3>=1000
2026-01-29 15:10:12,415 INFO CombineRules :: it. 4>=1000 | ((rel X:5.9e+00>=2.5e-01 | rel Y:4.9e-01>=2.5e-01 ) & kappa:2.0e+00) | it. 4>=1000
2026-01-29 15:10:12,557 INFO CombineRules :: it. 5>=1000 | ((rel X:4.5e+00>=2.5e-01 | rel Y:4.0e-01>=2.5e-01 ) & kappa:3.0e+00) | it. 5>=1000
2026-01-29 15:10:12,735 INFO CombineRules :: it. 6>=1000 | ((rel X:3.5e+00>=2.5e-01 | rel Y:3.5e-01>=2.5e-01 ) & kappa:4.7e+00) | it. 6>=1000
2026-01-29 15:10:12,903 INFO CombineRules :: it. 7>=1000 | ((rel X:2.7e+00>=2.5e-01 | rel Y:3.1e-01>=2.5e-01 ) & kappa:5.0e+00) | it. 7>=1000
2026-01-29 15:10:13,052 INFO CombineRules :: it. 8>=1000 | ((rel X:2.1e+00>=2.5e-01 | rel Y:2.8e-01>=2.5e-01 ) & kappa:5.0e+00) | it. 8>=1000
2026-01-29 15:10:13,197 INFO CombineRules :: it. 9>=1000 | ((rel X:1.7e+00>=2.5e-01 | rel Y:2.5e-01>=2.5e-01 [Rule RelTolYStop(0.3333333333333333) triggered.]) & kappa:4.5e+00[All rules triggered.]) | it. 9>=1000
2026-01-29 15:10:13,966 INFO CountIterations :: it. 3>=5
2026-01-29 15:10:14,089 INFO CombineRules :: it. 0>=1000 | ((rel X:--(x=0)! | rel Y:--(y=0) ) & kappa:1.0e+00) | it. 0>=1000
2026-01-29 15:10:14,161 INFO CombineRules :: it. 1>=1000 | ((rel X:2.2e+02>=2.5e-01 | rel Y:1.1e+01>=2.5e-01 ) & kappa:1.4e+00) | it. 1>=1000
2026-01-29 15:10:14,236 INFO CombineRules :: it. 2>=1000 | ((rel X:7.7e+01>=2.5e-01 | rel Y:5.0e+00>=2.5e-01 ) & kappa:1.4e+00) | it. 2>=1000
2026-01-29 15:10:14,309 INFO CombineRules :: it. 3>=1000 | ((rel X:4.0e+01>=2.5e-01 | rel Y:3.0e+00>=2.5e-01 ) & kappa:1.6e+00) | it. 3>=1000
2026-01-29 15:10:14,381 INFO CombineRules :: it. 4>=1000 | ((rel X:2.5e+01>=2.5e-01 | rel Y:2.0e+00>=2.5e-01 ) & kappa:1.9e+00) | it. 4>=1000
2026-01-29 15:10:14,454 INFO CombineRules :: it. 5>=1000 | ((rel X:1.8e+01>=2.5e-01 | rel Y:1.5e+00>=2.5e-01 ) & kappa:2.5e+00) | it. 5>=1000
2026-01-29 15:10:14,536 INFO CombineRules :: it. 6>=1000 | ((rel X:1.4e+01>=2.5e-01 | rel Y:1.2e+00>=2.5e-01 ) & kappa:3.2e+00) | it. 6>=1000
2026-01-29 15:10:14,609 INFO CombineRules :: it. 7>=1000 | ((rel X:1.1e+01>=2.5e-01 | rel Y:1.0e+00>=2.5e-01 ) & kappa:3.6e+00) | it. 7>=1000
2026-01-29 15:10:14,679 INFO CombineRules :: it. 8>=1000 | ((rel X:8.6e+00>=2.5e-01 | rel Y:9.1e-01>=2.5e-01 ) & kappa:4.3e+00) | it. 8>=1000
2026-01-29 15:10:14,751 INFO CombineRules :: it. 9>=1000 | ((rel X:6.9e+00>=2.5e-01 | rel Y:8.0e-01>=2.5e-01 ) & kappa:5.0e+00) | it. 9>=1000
2026-01-29 15:10:14,823 INFO CombineRules :: it. 10>=1000 | ((rel X:5.7e+00>=2.5e-01 | rel Y:7.2e-01>=2.5e-01 ) & kappa:5.3e+00) | it. 10>=1000
2026-01-29 15:10:14,927 INFO CombineRules :: it. 11>=1000 | ((rel X:4.8e+00>=2.5e-01 | rel Y:6.5e-01>=2.5e-01 ) & kappa:5.6e+00) | it. 11>=1000
2026-01-29 15:10:14,998 INFO CombineRules :: it. 12>=1000 | ((rel X:4.1e+00>=2.5e-01 | rel Y:5.9e-01>=2.5e-01 ) & kappa:5.7e+00) | it. 12>=1000
2026-01-29 15:10:15,070 INFO CombineRules :: it. 13>=1000 | ((rel X:3.5e+00>=2.5e-01 | rel Y:5.3e-01>=2.5e-01 ) & kappa:5.4e+00) | it. 13>=1000
2026-01-29 15:10:15,142 INFO CombineRules :: it. 14>=1000 | ((rel X:3.0e+00>=2.5e-01 | rel Y:4.8e-01>=2.5e-01 ) & kappa:5.4e+00) | it. 14>=1000
2026-01-29 15:10:15,217 INFO CombineRules :: it. 15>=1000 | ((rel X:2.6e+00>=2.5e-01 | rel Y:4.3e-01>=2.5e-01 ) & kappa:5.2e+00) | it. 15>=1000
2026-01-29 15:10:15,292 INFO CombineRules :: it. 16>=1000 | ((rel X:2.2e+00>=2.5e-01 | rel Y:3.9e-01>=2.5e-01 ) & kappa:5.7e+00) | it. 16>=1000
2026-01-29 15:10:15,485 INFO CombineRules :: it. 17>=1000 | ((rel X:2.0e+00>=2.5e-01 | rel Y:3.6e-01>=2.5e-01 ) & kappa:6.2e+00) | it. 17>=1000
2026-01-29 15:10:15,559 INFO CombineRules :: it. 18>=1000 | ((rel X:1.8e+00>=2.5e-01 | rel Y:3.3e-01>=2.5e-01 ) & kappa:7.4e+00) | it. 18>=1000
2026-01-29 15:10:15,630 INFO CombineRules :: it. 19>=1000 | ((rel X:1.6e+00>=2.5e-01 | rel Y:3.1e-01>=2.5e-01 ) & kappa:7.4e+00) | it. 19>=1000
2026-01-29 15:10:15,702 INFO CombineRules :: it. 20>=1000 | ((rel X:1.5e+00>=2.5e-01 | rel Y:2.9e-01>=2.5e-01 ) & kappa:7.6e+00) | it. 20>=1000
2026-01-29 15:10:15,776 INFO CombineRules :: it. 21>=1000 | ((rel X:1.3e+00>=2.5e-01 | rel Y:2.7e-01>=2.5e-01 ) & kappa:8.5e+00) | it. 21>=1000
2026-01-29 15:10:15,862 INFO CombineRules :: it. 22>=1000 | ((rel X:1.2e+00>=2.5e-01 | rel Y:2.5e-01>=2.5e-01 ) & kappa:9.2e+00) | it. 22>=1000
2026-01-29 15:10:15,932 INFO CombineRules :: it. 23>=1000 | ((rel X:1.1e+00>=2.5e-01 | rel Y:2.4e-01>=2.5e-01 [Rule RelTolYStop(0.3333333333333333) triggered.]) & kappa:8.9e+00[All rules triggered.]) | it. 23>=1000
2026-01-29 15:10:16,605 INFO CountIterations :: it. 4>=5
2026-01-29 15:10:16,815 INFO CombineRules :: it. 0>=1000 | ((rel X:--(x=0)! | rel Y:--(y=0) ) & kappa:1.0e+00) | it. 0>=1000
2026-01-29 15:10:16,964 INFO CombineRules :: it. 1>=1000 | ((rel X:5.5e+02>=2.5e-01 | rel Y:1.7e+01>=2.5e-01 ) & kappa:1.3e+00) | it. 1>=1000
2026-01-29 15:10:17,096 INFO CombineRules :: it. 2>=1000 | ((rel X:2.2e+02>=2.5e-01 | rel Y:8.3e+00>=2.5e-01 ) & kappa:1.5e+00) | it. 2>=1000
2026-01-29 15:10:17,255 INFO CombineRules :: it. 3>=1000 | ((rel X:1.2e+02>=2.5e-01 | rel Y:5.2e+00>=2.5e-01 ) & kappa:1.7e+00) | it. 3>=1000
2026-01-29 15:10:17,379 INFO CombineRules :: it. 4>=1000 | ((rel X:7.6e+01>=2.5e-01 | rel Y:3.6e+00>=2.5e-01 ) & kappa:2.0e+00) | it. 4>=1000
2026-01-29 15:10:17,526 INFO CombineRules :: it. 5>=1000 | ((rel X:5.1e+01>=2.5e-01 | rel Y:2.6e+00>=2.5e-01 ) & kappa:2.2e+00) | it. 5>=1000
2026-01-29 15:10:17,661 INFO CombineRules :: it. 6>=1000 | ((rel X:3.6e+01>=2.5e-01 | rel Y:2.0e+00>=2.5e-01 ) & kappa:2.4e+00) | it. 6>=1000
2026-01-29 15:10:17,794 INFO CombineRules :: it. 7>=1000 | ((rel X:2.8e+01>=2.5e-01 | rel Y:1.6e+00>=2.5e-01 ) & kappa:2.9e+00) | it. 7>=1000
2026-01-29 15:10:17,950 INFO CombineRules :: it. 8>=1000 | ((rel X:2.3e+01>=2.5e-01 | rel Y:1.3e+00>=2.5e-01 ) & kappa:3.6e+00) | it. 8>=1000
2026-01-29 15:10:18,127 INFO CombineRules :: it. 9>=1000 | ((rel X:1.9e+01>=2.5e-01 | rel Y:1.2e+00>=2.5e-01 ) & kappa:5.0e+00) | it. 9>=1000
2026-01-29 15:10:18,270 INFO CombineRules :: it. 10>=1000 | ((rel X:1.6e+01>=2.5e-01 | rel Y:1.1e+00>=2.5e-01 ) & kappa:5.7e+00) | it. 10>=1000
2026-01-29 15:10:18,419 INFO CombineRules :: it. 11>=1000 | ((rel X:1.4e+01>=2.5e-01 | rel Y:9.8e-01>=2.5e-01 ) & kappa:6.1e+00) | it. 11>=1000
2026-01-29 15:10:18,571 INFO CombineRules :: it. 12>=1000 | ((rel X:1.2e+01>=2.5e-01 | rel Y:9.0e-01>=2.5e-01 ) & kappa:6.6e+00) | it. 12>=1000
2026-01-29 15:10:18,720 INFO CombineRules :: it. 13>=1000 | ((rel X:1.0e+01>=2.5e-01 | rel Y:8.2e-01>=2.5e-01 ) & kappa:6.1e+00) | it. 13>=1000
2026-01-29 15:10:18,867 INFO CombineRules :: it. 14>=1000 | ((rel X:8.7e+00>=2.5e-01 | rel Y:7.6e-01>=2.5e-01 ) & kappa:7.0e+00) | it. 14>=1000
2026-01-29 15:10:19,078 INFO CombineRules :: it. 15>=1000 | ((rel X:7.7e+00>=2.5e-01 | rel Y:7.1e-01>=2.5e-01 ) & kappa:8.8e+00) | it. 15>=1000
2026-01-29 15:10:19,250 INFO CombineRules :: it. 16>=1000 | ((rel X:6.8e+00>=2.5e-01 | rel Y:6.7e-01>=2.5e-01 ) & kappa:9.4e+00) | it. 16>=1000
2026-01-29 15:10:19,408 INFO CombineRules :: it. 17>=1000 | ((rel X:6.1e+00>=2.5e-01 | rel Y:6.4e-01>=2.5e-01 ) & kappa:1.1e+01) | it. 17>=1000
2026-01-29 15:10:19,548 INFO CombineRules :: it. 18>=1000 | ((rel X:5.4e+00>=2.5e-01 | rel Y:6.1e-01>=2.5e-01 ) & kappa:1.2e+01) | it. 18>=1000
2026-01-29 15:10:19,709 INFO CombineRules :: it. 19>=1000 | ((rel X:4.8e+00>=2.5e-01 | rel Y:5.8e-01>=2.5e-01 ) & kappa:1.1e+01) | it. 19>=1000
2026-01-29 15:10:19,907 INFO CombineRules :: it. 20>=1000 | ((rel X:4.3e+00>=2.5e-01 | rel Y:5.5e-01>=2.5e-01 ) & kappa:1.3e+01) | it. 20>=1000
2026-01-29 15:10:20,068 INFO CombineRules :: it. 21>=1000 | ((rel X:3.9e+00>=2.5e-01 | rel Y:5.3e-01>=2.5e-01 ) & kappa:1.3e+01) | it. 21>=1000
2026-01-29 15:10:20,216 INFO CombineRules :: it. 22>=1000 | ((rel X:3.5e+00>=2.5e-01 | rel Y:5.1e-01>=2.5e-01 ) & kappa:1.2e+01) | it. 22>=1000
2026-01-29 15:10:20,362 INFO CombineRules :: it. 23>=1000 | ((rel X:3.2e+00>=2.5e-01 | rel Y:4.9e-01>=2.5e-01 ) & kappa:1.4e+01) | it. 23>=1000
2026-01-29 15:10:20,504 INFO CombineRules :: it. 24>=1000 | ((rel X:2.9e+00>=2.5e-01 | rel Y:4.7e-01>=2.5e-01 ) & kappa:1.3e+01) | it. 24>=1000
2026-01-29 15:10:20,681 INFO CombineRules :: it. 25>=1000 | ((rel X:2.6e+00>=2.5e-01 | rel Y:4.5e-01>=2.5e-01 ) & kappa:1.3e+01) | it. 25>=1000
2026-01-29 15:10:20,829 INFO CombineRules :: it. 26>=1000 | ((rel X:2.4e+00>=2.5e-01 | rel Y:4.3e-01>=2.5e-01 ) & kappa:1.2e+01) | it. 26>=1000
2026-01-29 15:10:20,976 INFO CombineRules :: it. 27>=1000 | ((rel X:2.2e+00>=2.5e-01 | rel Y:4.1e-01>=2.5e-01 ) & kappa:1.2e+01) | it. 27>=1000
2026-01-29 15:10:21,128 INFO CombineRules :: it. 28>=1000 | ((rel X:2.0e+00>=2.5e-01 | rel Y:3.9e-01>=2.5e-01 ) & kappa:1.1e+01) | it. 28>=1000
2026-01-29 15:10:21,272 INFO CombineRules :: it. 29>=1000 | ((rel X:1.9e+00>=2.5e-01 | rel Y:3.7e-01>=2.5e-01 ) & kappa:1.0e+01) | it. 29>=1000
2026-01-29 15:10:21,420 INFO CombineRules :: it. 30>=1000 | ((rel X:1.7e+00>=2.5e-01 | rel Y:3.5e-01>=2.5e-01 ) & kappa:1.1e+01) | it. 30>=1000
2026-01-29 15:10:21,569 INFO CombineRules :: it. 31>=1000 | ((rel X:1.6e+00>=2.5e-01 | rel Y:3.3e-01>=2.5e-01 ) & kappa:1.0e+01) | it. 31>=1000
2026-01-29 15:10:21,720 INFO CombineRules :: it. 32>=1000 | ((rel X:1.5e+00>=2.5e-01 | rel Y:3.2e-01>=2.5e-01 ) & kappa:1.0e+01) | it. 32>=1000
2026-01-29 15:10:21,853 INFO CombineRules :: it. 33>=1000 | ((rel X:1.4e+00>=2.5e-01 | rel Y:3.0e-01>=2.5e-01 ) & kappa:1.1e+01) | it. 33>=1000
2026-01-29 15:10:21,993 INFO CombineRules :: it. 34>=1000 | ((rel X:1.3e+00>=2.5e-01 | rel Y:2.9e-01>=2.5e-01 ) & kappa:1.1e+01) | it. 34>=1000
2026-01-29 15:10:22,148 INFO CombineRules :: it. 35>=1000 | ((rel X:1.2e+00>=2.5e-01 | rel Y:2.8e-01>=2.5e-01 ) & kappa:1.2e+01) | it. 35>=1000
2026-01-29 15:10:22,285 INFO CombineRules :: it. 36>=1000 | ((rel X:1.2e+00>=2.5e-01 | rel Y:2.7e-01>=2.5e-01 ) & kappa:1.4e+01) | it. 36>=1000
2026-01-29 15:10:22,438 INFO CombineRules :: it. 37>=1000 | ((rel X:1.1e+00>=2.5e-01 | rel Y:2.6e-01>=2.5e-01 ) & kappa:1.5e+01) | it. 37>=1000
2026-01-29 15:10:22,585 INFO CombineRules :: it. 38>=1000 | ((rel X:1.0e+00>=2.5e-01 | rel Y:2.5e-01>=2.5e-01 [Rule RelTolYStop(0.3333333333333333) triggered.]) & kappa:1.5e+01[All rules triggered.]) | it. 38>=1000
2026-01-29 15:10:23,355 INFO CountIterations :: it. 5>=5