[1]:
import numpy as np
import matplotlib.pyplot as plt
from regpy.operators import Operator
from regpy.vecsps import UniformGridFcts
Volterra example with iterative regularised Gauss-Newton semismooth solver¶
The discrete Volterra operator. The Volterra operator \(V_n\) is defined as
Its discrete form, using a Riemann sum, is simply
where \(h\) is the grid spacing. \(V_1\) is linear.
Therefore, we create a subclass of regpy.Operator type in the next code block. In the following create new operators of that type can simply be done by initiating with that class. This class will have the following parameters. (Side remark you may also do the definition in a separate file for this example check out volterra.py in this example folder. )
Parameters¶
domain : regpy.vecsps.UniformGridFcts > The domain on which the operator is defined. Must be one-dimensional.
exponent : float > The exponent (n). Default is 1.
[2]:
class Volterra(Operator):
def __init__(self, domain, exponent=1):
assert isinstance(domain, UniformGridFcts)
assert domain.ndim == 1
self.exponent = exponent
"""The exponent."""
super().__init__(domain, domain, linear=(exponent == 1))
def _eval(self, x, differentiate=False):
if differentiate:
self._factor = self.exponent * x**(self.exponent - 1)
return self.domain.volume_elem * np.cumsum(x**self.exponent)
def _derivative(self, x):
return self.domain.volume_elem * np.cumsum(self._factor * x)
def _adjoint(self, y):
x = self.domain.volume_elem * np.flipud(np.cumsum(np.flipud(y)))
if self.linear:
return x
else:
return self._factor * x
Initialization¶
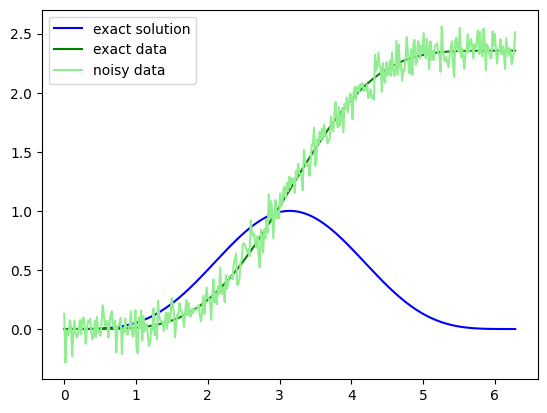
Having generally defined the Volterra operator above construct an explicit Volterra operator with exponent \(n=2\) on the interval \([0,2\pi]\) discretized by a UniformGridFcts with 200 points. Note, the operator will be non-linear operator since the exponent is not \(1\). Moreover, we choose the exact solution
for which the exact data is given by
Additionally we construct noise by sampling in the codomain a random vector. This noise \(\nu\) is then added to the exact data giving our noisy data \(g^\delta = g^\dagger + \nu\).
[3]:
grid = UniformGridFcts(np.linspace(0, 2 * np.pi, 400))
op = Volterra(grid,exponent=2)
exact_solution = (1-np.cos(grid.coords[0]))**2/4
plt.figure()
plt.plot(grid.coords[0],exact_solution,color="blue",label='exact solution')
exact_data = (3*grid.coords[0] - 4*np.sin(grid.coords[0]) + np.cos(grid.coords[0])*np.sin(grid.coords[0]))/8
noise = 0.1 * op.codomain.randn()
data = exact_data + noise
plt.plot(grid.coords[0], exact_data, color="green", label='exact data')
plt.plot(grid.coords[0], data, color="lightgreen", label='noisy data')
plt.legend()
print("Maximal error of operator evaluation on exact solution to exact data: {:.4E}".format(np.max(np.abs(op(exact_solution)-exact_data))))
plt.show()
Maximal error of operator evaluation on exact solution to exact data: 6.3814E-01
Regularization¶
First we define the regularization setting using the Setting and choosing \(L^2\) spaces defined on the UniformGridFcts. This setting is a general container which then can be used with solvers.
[4]:
from regpy.hilbert import L2
from regpy.solvers import Setting
setting = Setting(
op=op,
penalty=L2,
data_fid=L2,
data= data,
regpar= 1.)
As a next step we choose an initial guess, in this case we choose something that is almost zero. Then using the setting and init information we can setup non-linear solver, which is the NewtonSemiSmoothFrozen. Which aims to solve the quadratic Tikhonov functionals
subject to bilateral constraints \(\psi_- \leq x \leq \psi_+\) in each step by linearizing the equation at the current iterate. The regularization parameter will be sequentially lowered using a geometric sequence which can be done by giving the tuple alpha = (alpha0,q) that creates the sequence \((\alpha_0 q^n)_{n=0,1,2,...}\) For our example we choose \(\psi_- = 0\) and \(\psi_+ = 1.1\) as constraints. Having these we only need to set an upper limit on the inner iterations
which we choose to be 10.
[5]:
from regpy.solvers.nonlinear import NewtonSemiSmoothFrozen
init = op.domain.ones()*0.00005
psi_minus = op.domain.ones()*0.0
psi_plus = op.domain.ones()*1.1
solver = NewtonSemiSmoothFrozen(
setting,
data,
alphas = (1,0.9),
psi_minus= psi_minus,
psi_plus=psi_plus,
init = init,
inner_NSS_iter_max=10)
We stop the iterative algorithm after at most \(100\) steps and have as early stopping criterion the discrepancy rule implemented. This can be easily done by summing the two instances of the regpy.stoprules.
[6]:
import regpy.stoprules as rules
stoprule = (
rules.CountIterations(100) +
rules.Discrepancy(
setting.h_codomain.norm, data,
noiselevel=setting.h_codomain.norm(noise),
tau=1.4
)
)
2026-01-29 15:10:38,103 WARNING Discrepancy :: Initialization of Discrepancy with two positional arguments (norm, data) deprecated. Use one positional argument (noiselevel) and specifiy norm and data via a keyword argument setting!
After everything is defined we can run the solver with the specified stopping rule using the method run() of the solver. However, in the following we use the until() which and extract the yielding elements to construct a nice output.
[7]:
recos = []
recos_data = []
for reco, reco_data in solver.until(stoprule):
recos.append(1*reco)
recos_data.append(reco_data)
2026-01-29 15:10:38,114 WARNING Setting :: Setting does not contain any explicit data.
2026-01-29 15:10:38,115 WARNING Setting :: Overwriting existing data in setting!
2026-01-29 15:10:38,116 WARNING TikhonovCG :: Providing xref as an argument to the CG solver is deprecated. Please provide it via the setting. Results may not be consistent!
2026-01-29 15:10:38,118 INFO CombineRules :: it. 0>=1000 | (abs X:1.4e-03>=1.0e-03 & rel X:--(x=0)! & kappa:1.0e+00)
2026-01-29 15:10:38,119 INFO CombineRules :: it. 1>=1000 | (abs X:1.7e-11>=1.0e-03 & rel X:1.3e-08>=9.9e-03 & kappa:1.0e+00[All rules triggered.])
Rule AndCombineRules([TolStop(0.001), RelTolXStop(0.01), KappaTrackAndMinIt(0)]) triggered.
2026-01-29 15:10:38,120 INFO CountIterations :: it. 0>=10
2026-01-29 15:10:38,121 INFO CombineRules :: it. 0>=100 | discr./noiselevel = 15.28< 1.40
2026-01-29 15:10:38,123 WARNING Setting :: Setting does not contain any explicit data.
2026-01-29 15:10:38,124 WARNING Setting :: Overwriting existing data in setting!
2026-01-29 15:10:38,125 WARNING TikhonovCG :: Providing xref as an argument to the CG solver is deprecated. Please provide it via the setting. Results may not be consistent!
2026-01-29 15:10:38,127 INFO CombineRules :: it. 0>=1000 | (abs X:2.1e-02>=1.1e-03 & rel X:--(x=0)! & kappa:1.0e+00)
2026-01-29 15:10:38,128 INFO CombineRules :: it. 1>=1000 | (abs X:6.7e-08>=1.1e-03 & rel X:3.2e-06>=9.9e-03 & kappa:1.0e+00[All rules triggered.])
Rule AndCombineRules([TolStop(0.0010540925533894599), RelTolXStop(0.01), KappaTrackAndMinIt(0)]) triggered.
2026-01-29 15:10:38,129 INFO CountIterations :: it. 0>=10
2026-01-29 15:10:38,130 INFO CombineRules :: it. 1>=100 | discr./noiselevel = 15.27< 1.40
2026-01-29 15:10:38,132 WARNING Setting :: Setting does not contain any explicit data.
2026-01-29 15:10:38,132 WARNING Setting :: Overwriting existing data in setting!
2026-01-29 15:10:38,133 WARNING TikhonovCG :: Providing xref as an argument to the CG solver is deprecated. Please provide it via the setting. Results may not be consistent!
2026-01-29 15:10:38,135 INFO CombineRules :: it. 0>=1000 | (abs X:3.8e-01>=1.1e-03 & rel X:--(x=0)! & kappa:1.0e+00)
2026-01-29 15:10:38,136 INFO CombineRules :: it. 1>=1000 | (abs X:3.5e-04>=1.1e-03 & rel X:9.3e-04>=9.9e-03 & kappa:1.0e+00[All rules triggered.])
Rule AndCombineRules([TolStop(0.0011111111111111111), RelTolXStop(0.01), KappaTrackAndMinIt(0)]) triggered.
2026-01-29 15:10:38,138 INFO CountIterations :: it. 0>=10
2026-01-29 15:10:38,139 INFO CombineRules :: it. 2>=100 | discr./noiselevel = 14.13< 1.40
2026-01-29 15:10:38,140 WARNING Setting :: Setting does not contain any explicit data.
2026-01-29 15:10:38,141 WARNING Setting :: Overwriting existing data in setting!
2026-01-29 15:10:38,142 WARNING TikhonovCG :: Providing xref as an argument to the CG solver is deprecated. Please provide it via the setting. Results may not be consistent!
2026-01-29 15:10:38,144 INFO CombineRules :: it. 0>=1000 | (abs X:6.7e+00>=1.2e-03 & rel X:--(x=0)! & kappa:1.0e+00)
2026-01-29 15:10:38,145 INFO CombineRules :: it. 1>=1000 | (abs X:5.3e-01>=1.2e-03 & rel X:3.5e-01>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,146 INFO CombineRules :: it. 2>=1000 | (abs X:1.6e-02>=1.2e-03 & rel X:9.9e-03>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,151 INFO CombineRules :: it. 3>=1000 | (abs X:2.4e-04>=1.2e-03 & rel X:1.5e-04>=9.9e-03 & kappa:1.0e+00[All rules triggered.])
Rule AndCombineRules([TolStop(0.001171213948210511), RelTolXStop(0.01), KappaTrackAndMinIt(0)]) triggered.
2026-01-29 15:10:38,152 INFO CountIterations :: it. 0>=10
2026-01-29 15:10:38,153 INFO CountIterations :: it. 1>=10
2026-01-29 15:10:38,155 WARNING Setting :: Setting does not contain any explicit data.
2026-01-29 15:10:38,155 WARNING Setting :: Overwriting existing data in setting!
2026-01-29 15:10:38,156 WARNING TikhonovCG :: Providing xref as an argument to the CG solver is deprecated. Please provide it via the setting. Results may not be consistent!
2026-01-29 15:10:38,158 INFO CombineRules :: it. 0>=1000 | (abs X:8.5e+00>=1.2e-03 & rel X:--(x=0)! & kappa:1.0e+00)
2026-01-29 15:10:38,159 INFO CombineRules :: it. 1>=1000 | (abs X:5.8e-01>=1.2e-03 & rel X:3.1e-01>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,160 INFO CombineRules :: it. 2>=1000 | (abs X:1.9e-02>=1.2e-03 & rel X:9.5e-03>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,161 INFO CombineRules :: it. 3>=1000 | (abs X:3.3e-04>=1.2e-03 & rel X:1.7e-04>=9.9e-03 & kappa:1.0e+00[All rules triggered.])
Rule AndCombineRules([TolStop(0.001171213948210511), RelTolXStop(0.01), KappaTrackAndMinIt(0)]) triggered.
2026-01-29 15:10:38,162 INFO CountIterations :: it. 2>=10
2026-01-29 15:10:38,163 WARNING Setting :: Setting does not contain any explicit data.
2026-01-29 15:10:38,164 WARNING Setting :: Overwriting existing data in setting!
2026-01-29 15:10:38,165 WARNING TikhonovCG :: Providing xref as an argument to the CG solver is deprecated. Please provide it via the setting. Results may not be consistent!
2026-01-29 15:10:38,167 INFO CombineRules :: it. 0>=1000 | (abs X:1.1e-01>=1.2e-03 & rel X:--(x=0)! & kappa:1.0e+00)
2026-01-29 15:10:38,168 INFO CombineRules :: it. 1>=1000 | (abs X:6.0e-03>=1.2e-03 & rel X:2.0e-01>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,170 INFO CombineRules :: it. 2>=1000 | (abs X:8.4e-05>=1.2e-03 & rel X:2.7e-03>=9.9e-03 & kappa:1.0e+00[All rules triggered.])
Rule AndCombineRules([TolStop(0.001171213948210511), RelTolXStop(0.01), KappaTrackAndMinIt(0)]) triggered.
2026-01-29 15:10:38,171 INFO CountIterations :: it. 3>=10
2026-01-29 15:10:38,173 WARNING Setting :: Setting does not contain any explicit data.
2026-01-29 15:10:38,174 WARNING Setting :: Overwriting existing data in setting!
2026-01-29 15:10:38,175 WARNING TikhonovCG :: Providing xref as an argument to the CG solver is deprecated. Please provide it via the setting. Results may not be consistent!
2026-01-29 15:10:38,177 INFO CombineRules :: it. 0>=1000 | (abs X:2.6e-03>=1.2e-03 & rel X:--(x=0)! & kappa:1.0e+00)
2026-01-29 15:10:38,179 INFO CombineRules :: it. 1>=1000 | (abs X:1.2e-04>=1.2e-03 & rel X:1.6e-01>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,181 INFO CombineRules :: it. 2>=1000 | (abs X:5.3e-06>=1.2e-03 & rel X:7.0e-03>=9.9e-03 & kappa:1.0e+00[All rules triggered.])
Rule AndCombineRules([TolStop(0.001171213948210511), RelTolXStop(0.01), KappaTrackAndMinIt(0)]) triggered.
2026-01-29 15:10:38,182 INFO CountIterations :: it. 4>=10
2026-01-29 15:10:38,183 WARNING Setting :: Setting does not contain any explicit data.
2026-01-29 15:10:38,184 WARNING Setting :: Overwriting existing data in setting!
2026-01-29 15:10:38,188 WARNING TikhonovCG :: Providing xref as an argument to the CG solver is deprecated. Please provide it via the setting. Results may not be consistent!
2026-01-29 15:10:38,189 INFO CombineRules :: it. 0>=1000 | (abs X:1.1e-05>=1.2e-03 & rel X:--(x=0)! & kappa:1.0e+00)
2026-01-29 15:10:38,191 INFO CombineRules :: it. 1>=1000 | (abs X:3.6e-06>=1.2e-03 & rel X:9.9e-01>=9.9e-03 & kappa:1.1e+00)
2026-01-29 15:10:38,192 INFO CombineRules :: it. 2>=1000 | (abs X:1.7e-07>=1.2e-03 & rel X:3.0e-02>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,193 INFO CombineRules :: it. 3>=1000 | (abs X:2.4e-09>=1.2e-03 & rel X:4.3e-04>=9.9e-03 & kappa:1.0e+00[All rules triggered.])
Rule AndCombineRules([TolStop(0.001171213948210511), RelTolXStop(0.01), KappaTrackAndMinIt(0)]) triggered.
2026-01-29 15:10:38,194 INFO CountIterations :: it. 5>=10
2026-01-29 15:10:38,194 INFO CombineRules :: it. 3>=100 | discr./noiselevel = 15.11< 1.40
2026-01-29 15:10:38,196 WARNING Setting :: Setting does not contain any explicit data.
2026-01-29 15:10:38,197 WARNING Setting :: Overwriting existing data in setting!
2026-01-29 15:10:38,198 WARNING TikhonovCG :: Providing xref as an argument to the CG solver is deprecated. Please provide it via the setting. Results may not be consistent!
2026-01-29 15:10:38,199 INFO CombineRules :: it. 0>=1000 | (abs X:4.4e+01>=1.2e-03 & rel X:--(x=0)! & kappa:1.0e+00)
2026-01-29 15:10:38,200 INFO CombineRules :: it. 1>=1000 | (abs X:2.3e+00>=1.2e-03 & rel X:4.6e+00>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,202 INFO CombineRules :: it. 2>=1000 | (abs X:2.7e-01>=1.2e-03 & rel X:4.4e-01>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,202 INFO CombineRules :: it. 3>=1000 | (abs X:6.3e-02>=1.2e-03 & rel X:1.0e-01>=9.9e-03 & kappa:1.1e+00)
2026-01-29 15:10:38,204 INFO CombineRules :: it. 4>=1000 | (abs X:1.1e-02>=1.2e-03 & rel X:1.8e-02>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,205 INFO CombineRules :: it. 5>=1000 | (abs X:1.8e-03>=1.2e-03 & rel X:2.9e-03>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,206 INFO CombineRules :: it. 6>=1000 | (abs X:2.7e-04>=1.2e-03 & rel X:4.3e-04>=9.9e-03 & kappa:1.0e+00[All rules triggered.])
Rule AndCombineRules([TolStop(0.0012345679012345679), RelTolXStop(0.01), KappaTrackAndMinIt(0)]) triggered.
2026-01-29 15:10:38,207 INFO CountIterations :: it. 0>=10
2026-01-29 15:10:38,207 INFO CombineRules :: it. 4>=100 | discr./noiselevel = 3.42< 1.40
2026-01-29 15:10:38,209 WARNING Setting :: Setting does not contain any explicit data.
2026-01-29 15:10:38,209 WARNING Setting :: Overwriting existing data in setting!
2026-01-29 15:10:38,210 WARNING TikhonovCG :: Providing xref as an argument to the CG solver is deprecated. Please provide it via the setting. Results may not be consistent!
2026-01-29 15:10:38,212 INFO CombineRules :: it. 0>=1000 | (abs X:7.8e+00>=1.3e-03 & rel X:--(x=0)! & kappa:1.0e+00)
2026-01-29 15:10:38,213 INFO CombineRules :: it. 1>=1000 | (abs X:9.7e-01>=1.3e-03 & rel X:6.8e+00>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,214 INFO CombineRules :: it. 2>=1000 | (abs X:8.3e-02>=1.3e-03 & rel X:3.3e-01>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,215 INFO CombineRules :: it. 3>=1000 | (abs X:1.0e-02>=1.3e-03 & rel X:3.9e-02>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,215 INFO CombineRules :: it. 4>=1000 | (abs X:3.0e-03>=1.3e-03 & rel X:1.2e-02>=9.9e-03 & kappa:1.1e+00)
2026-01-29 15:10:38,216 INFO CombineRules :: it. 5>=1000 | (abs X:6.5e-04>=1.3e-03 & rel X:2.5e-03>=9.9e-03 & kappa:1.0e+00[All rules triggered.])
Rule AndCombineRules([TolStop(0.0013013488313450118), RelTolXStop(0.01), KappaTrackAndMinIt(0)]) triggered.
2026-01-29 15:10:38,217 INFO CountIterations :: it. 0>=10
2026-01-29 15:10:38,218 INFO CombineRules :: it. 5>=100 | discr./noiselevel = 1.43< 1.40
2026-01-29 15:10:38,219 WARNING Setting :: Setting does not contain any explicit data.
2026-01-29 15:10:38,220 WARNING Setting :: Overwriting existing data in setting!
2026-01-29 15:10:38,220 WARNING TikhonovCG :: Providing xref as an argument to the CG solver is deprecated. Please provide it via the setting. Results may not be consistent!
2026-01-29 15:10:38,223 INFO CombineRules :: it. 0>=1000 | (abs X:1.2e+00>=1.4e-03 & rel X:--(x=0)! & kappa:1.0e+00)
2026-01-29 15:10:38,224 INFO CombineRules :: it. 1>=1000 | (abs X:3.1e-01>=1.4e-03 & rel X:1.2e+01>=9.9e-03 & kappa:1.1e+00)
2026-01-29 15:10:38,225 INFO CombineRules :: it. 2>=1000 | (abs X:6.9e-02>=1.4e-03 & rel X:8.4e-01>=9.9e-03 & kappa:1.1e+00)
2026-01-29 15:10:38,226 INFO CombineRules :: it. 3>=1000 | (abs X:8.7e-03>=1.4e-03 & rel X:8.7e-02>=9.9e-03 & kappa:1.0e+00)
2026-01-29 15:10:38,227 INFO CombineRules :: it. 4>=1000 | (abs X:2.5e-03>=1.4e-03 & rel X:2.5e-02>=9.9e-03 & kappa:1.1e+00)
2026-01-29 15:10:38,228 INFO CombineRules :: it. 5>=1000 | (abs X:2.5e-04>=1.4e-03 & rel X:2.5e-03>=9.9e-03 & kappa:1.0e+00[All rules triggered.])
Rule AndCombineRules([TolStop(0.0013717421124828531), RelTolXStop(0.01), KappaTrackAndMinIt(0)]) triggered.
2026-01-29 15:10:38,229 INFO CountIterations :: it. 0>=10
2026-01-29 15:10:38,230 INFO CombineRules :: it. 6>=100 | discr./noiselevel = 1.32< 1.40
Rule Discrepancy(noiselevel=0.2518893045547308, tau=1.4) triggered.
Plotting¶
Finally, we plot the output.
[8]:
import matplotlib.animation
plt.rcParams["animation.html"] = "jshtml"
plt.rcParams['figure.dpi'] = 150
plt.ioff()
fig, axs = plt.subplots(1,2)
def animate(t):
axs[0].cla()
axs[0].plot(exact_solution,color="blue")
axs[0].plot(recos[t],color="lightblue")
axs[0].set_ylim(ymin=0,ymax=1.5)
axs[1].cla()
axs[1].plot(exact_data,color="green", label='exact')
axs[1].plot(recos_data[t],color="orange", label='reco')
axs[1].plot(data, color="lightgreen", label='measured')
axs[1].set_ylim(ymin=-0.2,ymax=2.5)
matplotlib.animation.FuncAnimation(fig, animate, frames=len(recos))
[8]: